Сетевой анализ
Основы геоинформатики: лекция 7
22 марта 2024 г.
Географические сети
Сетевые формы структурной организации явлений играют большую роль в географическое среде
Для моделирования таких структур используется теория графов.
Граф
Простой граф \(G(V,E)\) — совокупность множества вершин \(V = \{v_1, v_2, ...\}\) и множества ребер \(E\) (Newman 2018).
\(E\) состоит из упорядоченных пар элементов множества вершин:
\[ e_{ij} = \{v_i, v_j \},~ i \neq j \]
\(V\) не пусто;
\(E\) может быть пустым;
не все комбинации \(\{v_i, v_j \}\) могут входить в \(E\).
Матрица смежности
Представление ребер в виде матрицы \(A = \{a_{ij}\}\), где \(a_{ij} = 1\), если существует ребро \(e_{ij}\), и \(a_{ij} = 0\), если такого ребра нет.
\[ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} & 0 & 0 \\ 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \color{blue}{\mathbf 1} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \]
Матрица смежности
Представление ребер в виде матрицы \(A = \{a_{ij}\}\), где \(a_{ij} = 1\), если существует ребро \(e_{ij}\), и \(a_{ij} = 0\), если такого ребра нет.
\[ \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & 0 & 0 \\ 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & 0 & 0 & 0 \\ 0 & 0 & \color{red}{\mathbf 1} & \color{red}{\mathbf 1} & 0 & 0 & \color{red}{\mathbf 1} & 0 \\ \color{red}{\mathbf 1} & \color{red}{\mathbf 1} & 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & 0 \\ 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & \color{red}{\mathbf 1} & 0 & \color{red}{\mathbf 1} \\ 0 & 0 & 0 & 0 & 0 & 0 & \color{red}{\mathbf 1} & 0 \\ \end{bmatrix} \]
Топологическая эквивалентность
Топологически эквивалентными являются графы, у которых совпадают матрицы смежности (Barthelemy 2022).
Географические сети
Географические сети отличаются тем, что для них важную роль играет не только топологическая эквивалентность, но также местоположение (координаты) вершин.
Топологическая эквивалентность
Топологически эквивалентными являются графы, у которых совпадают матрицы смежности (Barthelemy 2022).
Географические сети
Географические сети отличаются тем, что для них важную роль играет не только топологическая эквивалентность, но также местоположение (координаты) вершин.
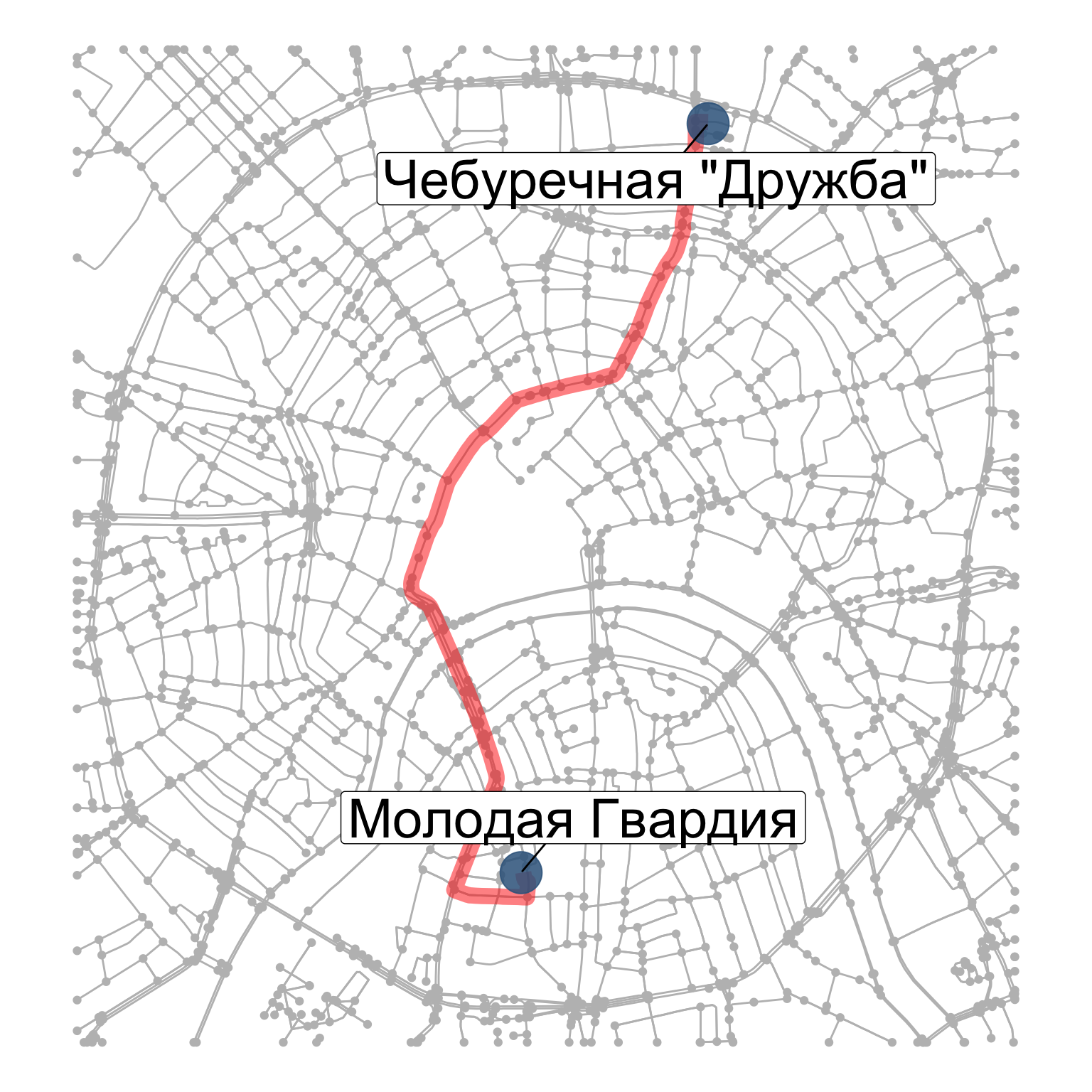
Кратчайший маршрут
Выполняется поиск последовательности ребер графа, которая дает минимальную стоимость передвижения между точками.
Особенности
стоимость одного ребра графа обычно выражается в времени передвижения по нему, либо его длине;
стоимость может быть масштабирована на коэффициент значимости ребра;
дополнительные задержки могут быть заложены в вершинах графа;
может учитываться трафик движения.
Задача коммивояжёра
Задача коммивояжера — определение оптимального маршрута объезда заданного множества точек
Использование
Одна из самых распространенных задач в логистике. Решается в целях оптимизации объезда клиентов, складов и т.д. Вычислительно является сложной задачей.
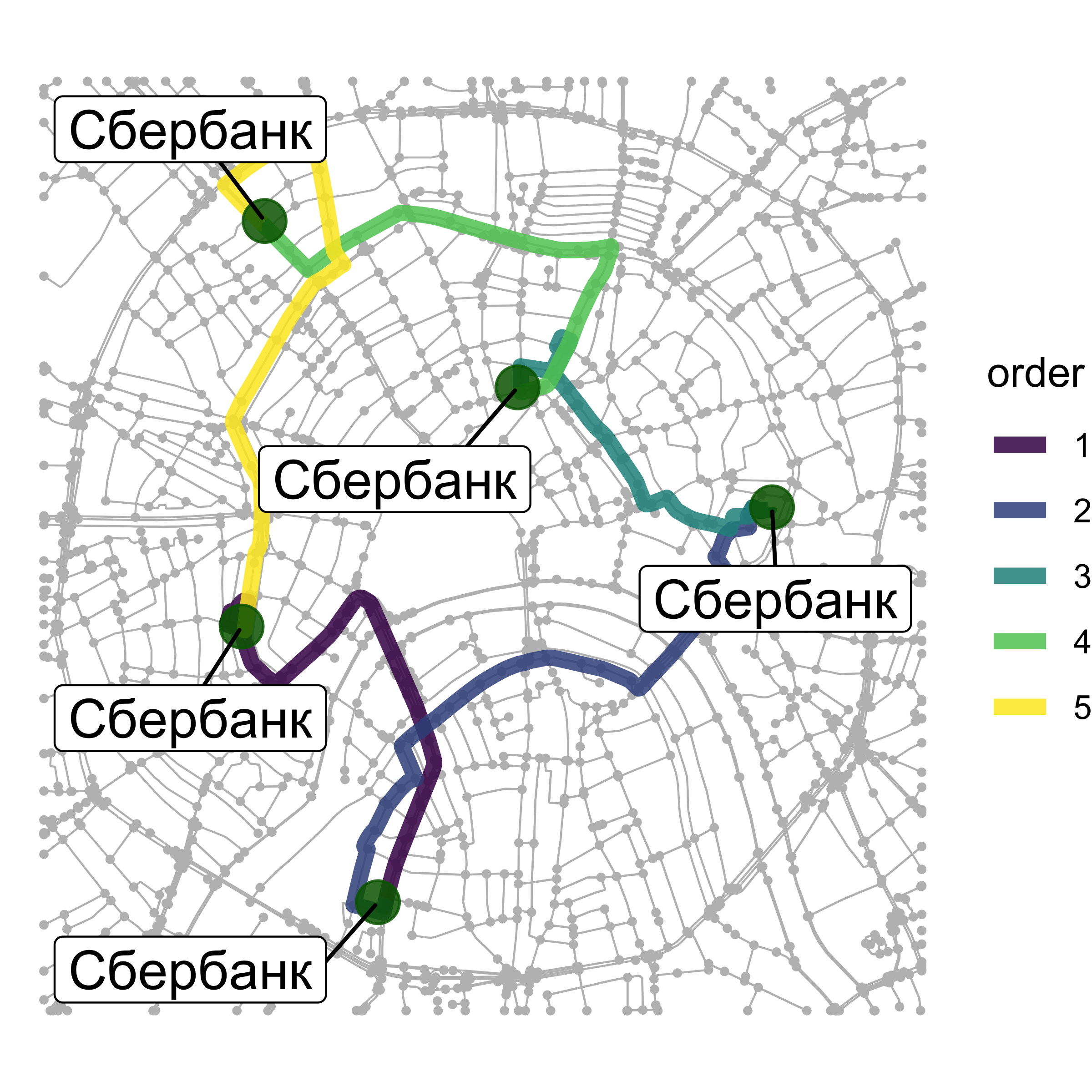
Ближайший пункт обслуживания
Задача данного класса позволяет находить для каждой точки клиента ближайший к ней пункт обслуживания
Пример
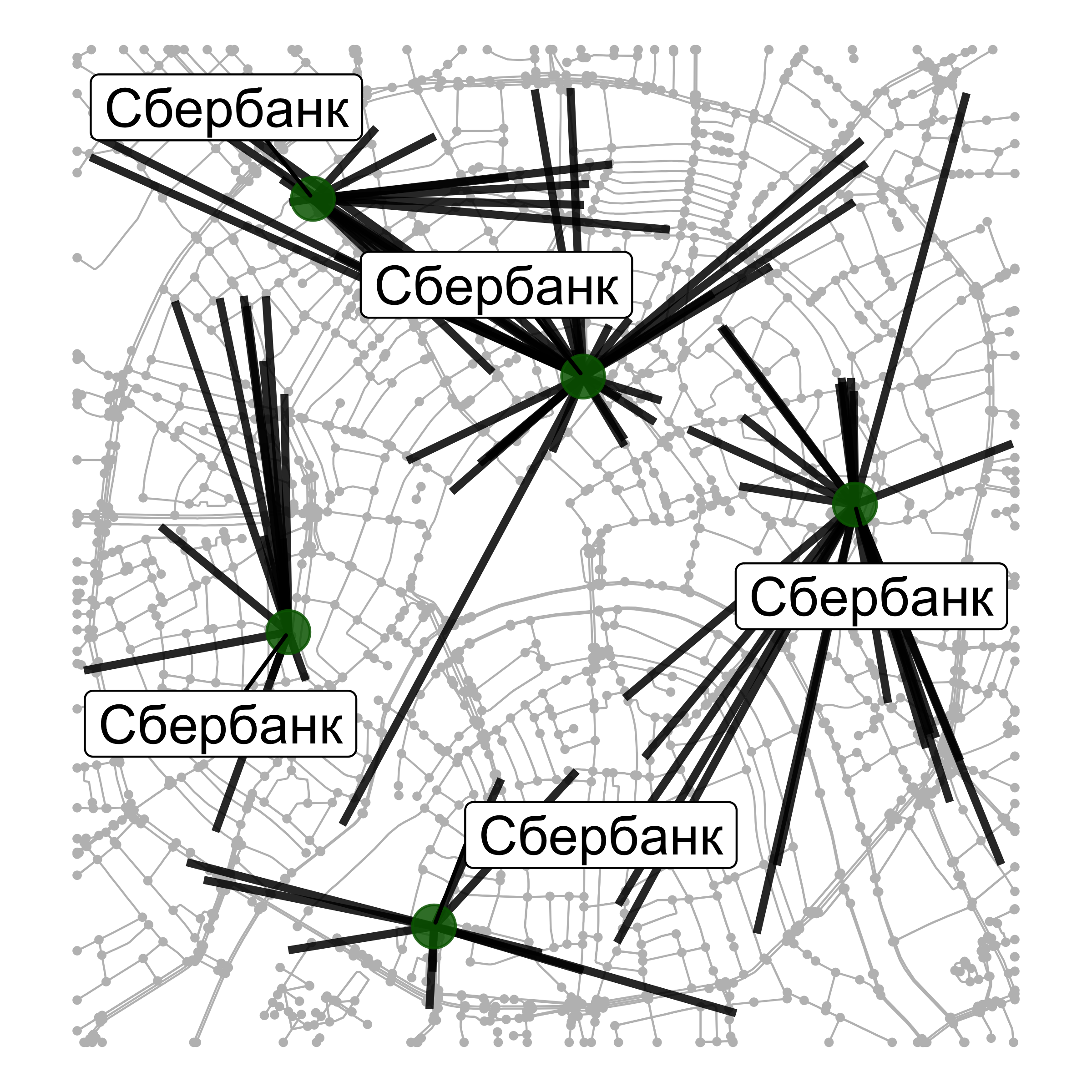
Для каждого заведения общепита найти ближайшее по времени отделение Сбербанка для пешехода
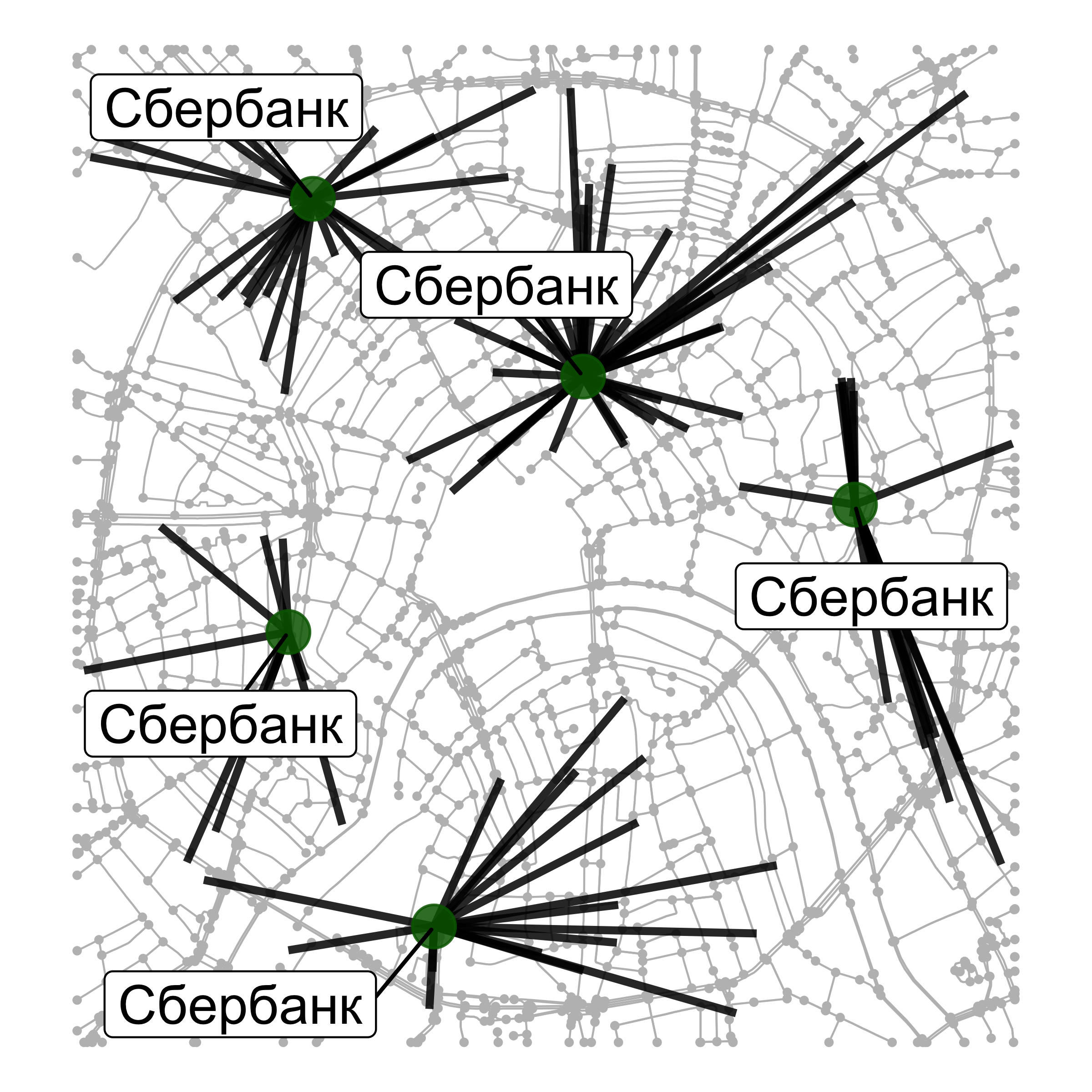
Ближайший пункт обслуживания
Задача данного класса позволяет находить для каждой точки клиента ближайший к ней пункт обслуживания
Пример
Для каждого заведения общепита найти ближайшее по времени отделение Сбербанка для автомобилиста
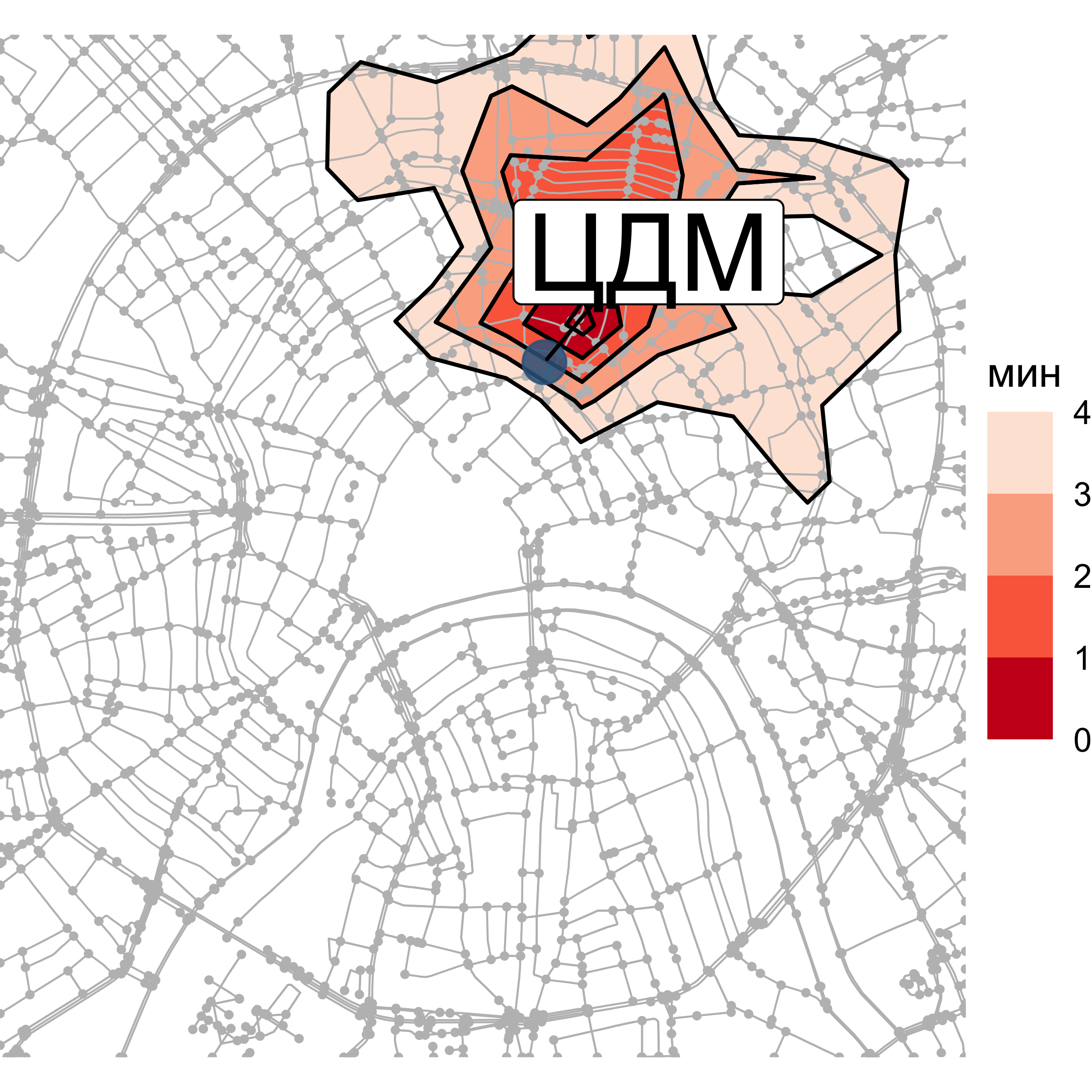
Изохроны
Изохрона — это линия постоянного времени движения от или до заданной точки.
Алгоритм построения
- В каждой вершине графа вычислить время движения от/до указанной точки.
- Собрать из вершин триангуляционное покрытие — поверхность времени движения.
- Извлечь из покрытия изолинии для заданных значений.
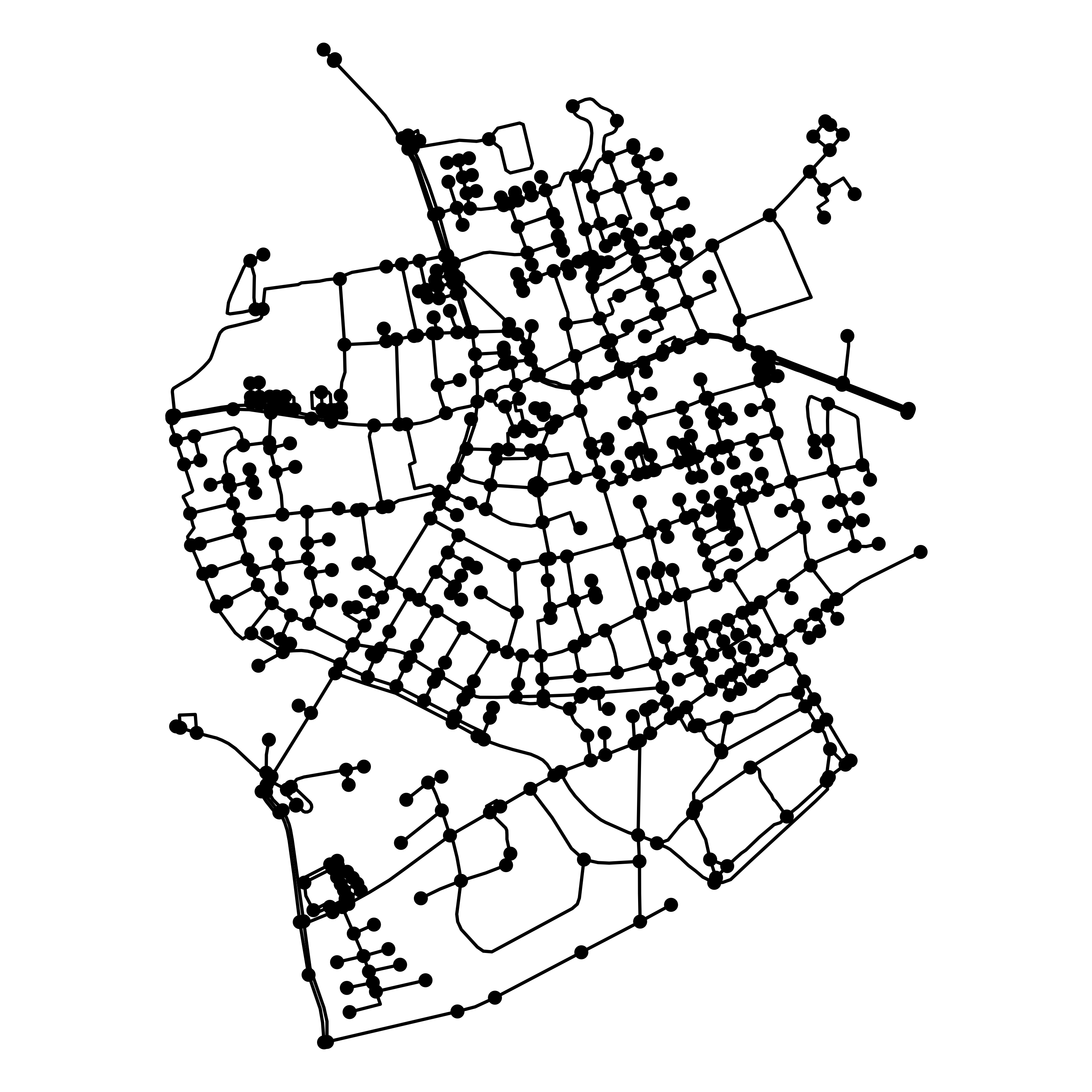
Анализ структуры
Анализ структуры географической сети охарактеризовать ее устройство в виде формальных показателей, определить топологические отношения и центральность отдельных элементов.
Центральность
Центральность — это важность элемента сети. Существует множество показателей центральности
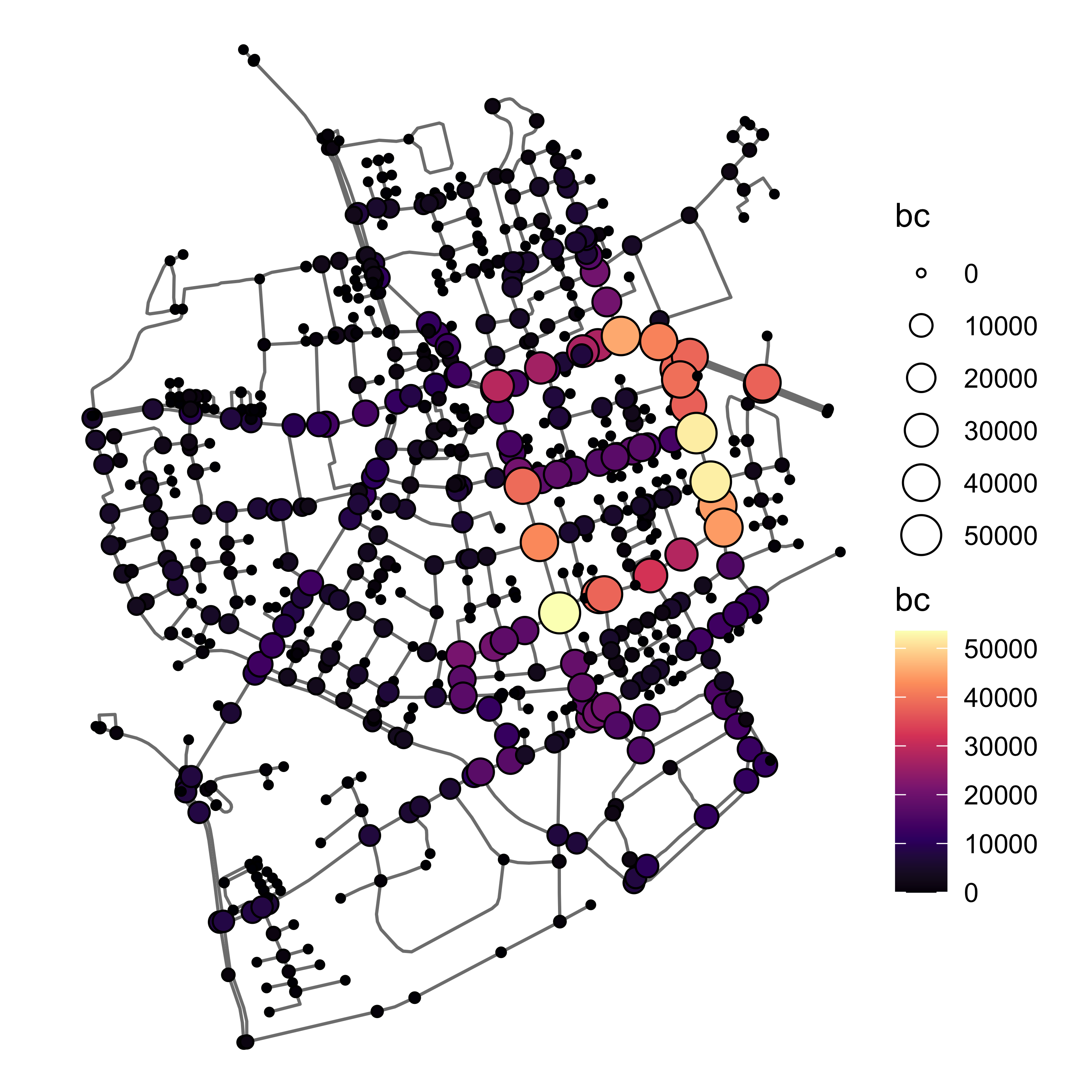
Центральность
Центральность по промежуточности показывает количество маршрутов, проходящих через узел/ребро.
Расчет и интерпретация
- Строятся маршруты между всеми возможными парами вершин в графе.
- В каждой вершине суммируется число прошедших через нее маршрутов.
Результат показывает основные магистрали в сети.
Центральность
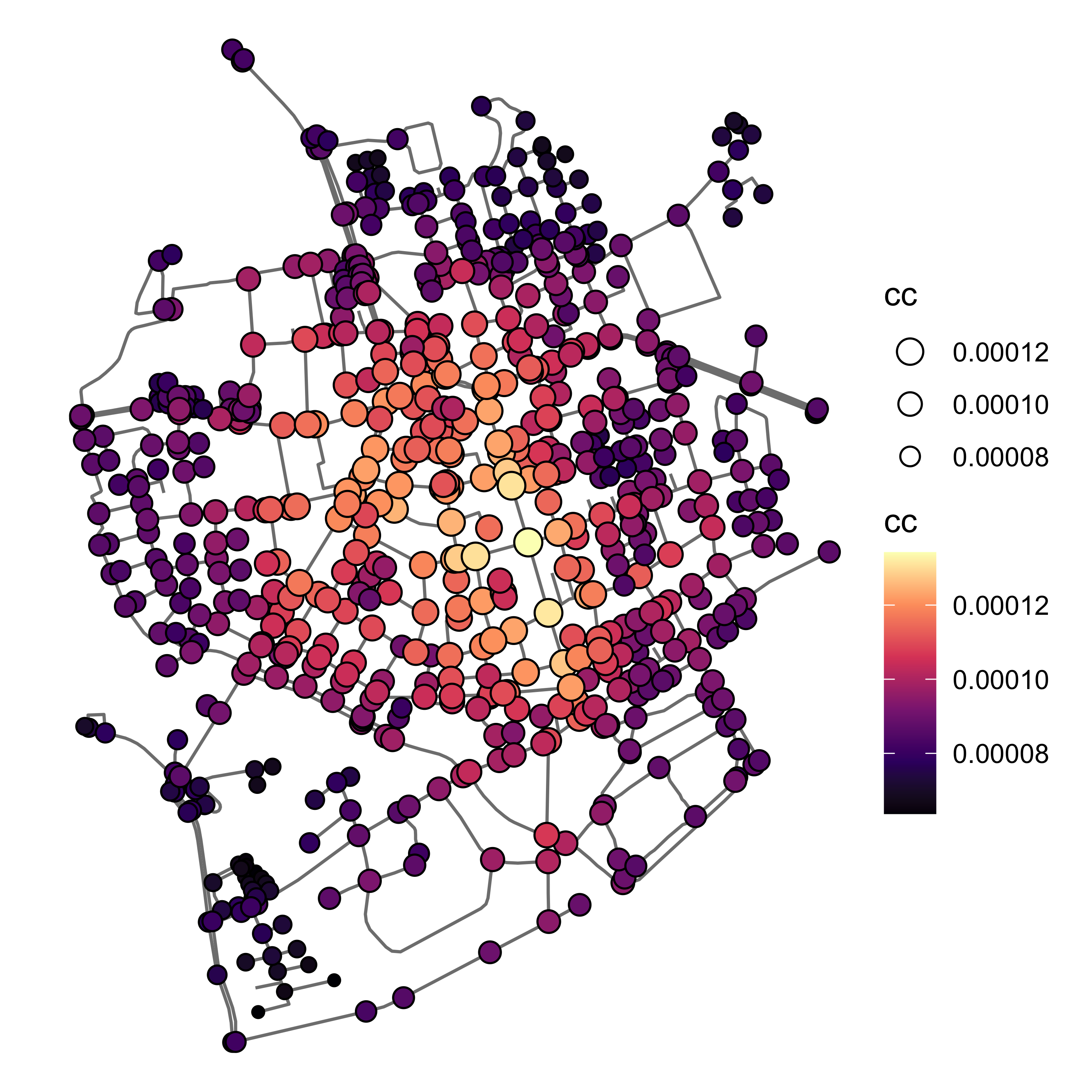
Центральность по близости обратно пропорциональна сумме расстояний от вершины до остальных вершин.
Интерпретация
Центральность по близости позволяет выделить условный “центр” сети — множество вершин, равноудаленных от всех остальных
Центральность
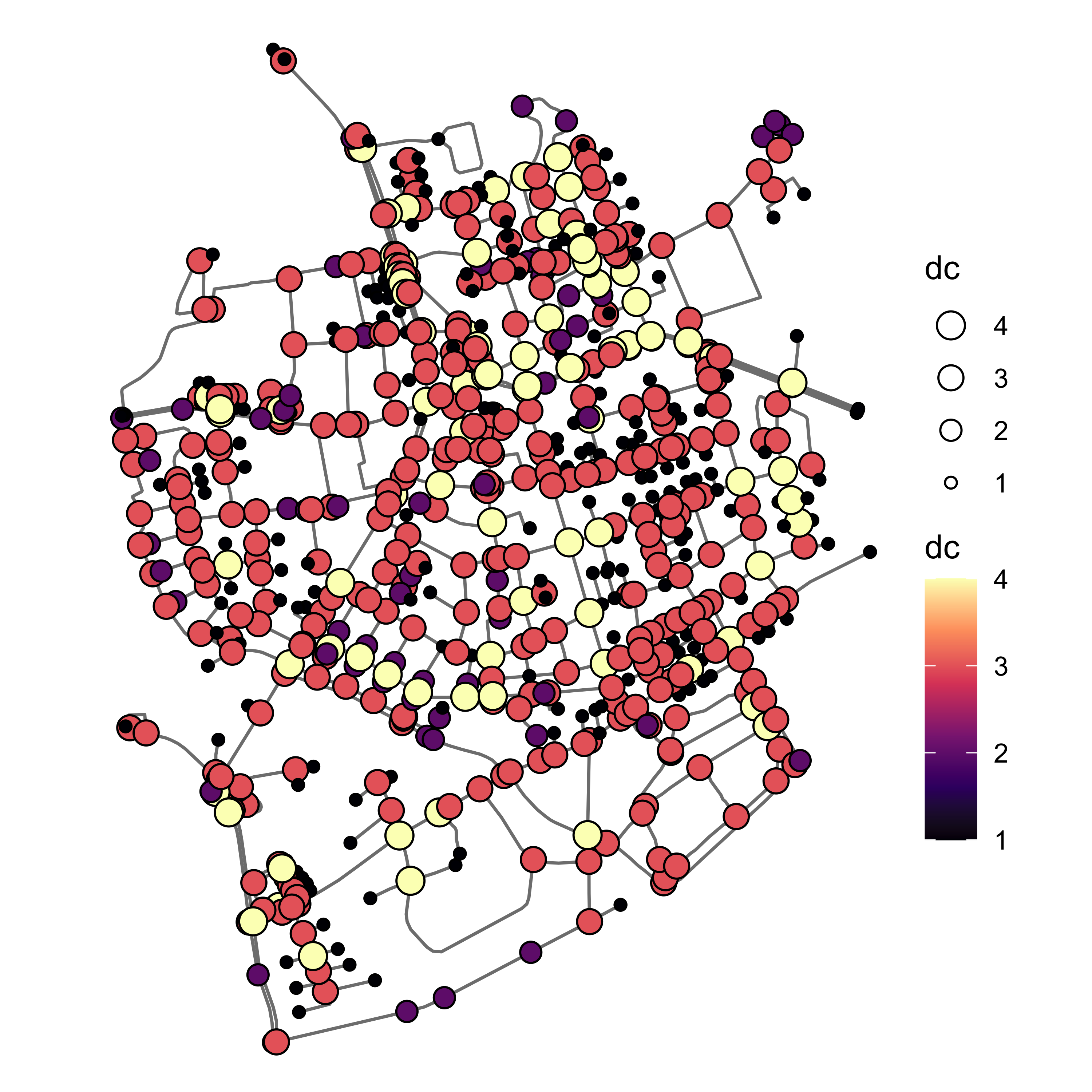
Центральность по степени показывает количество ребер, с которыми связана вершина.
Интерпретация
Центральность по степени является локальной характеристикой, она показывается важность вершины в ее собственной окрестности
Центральность
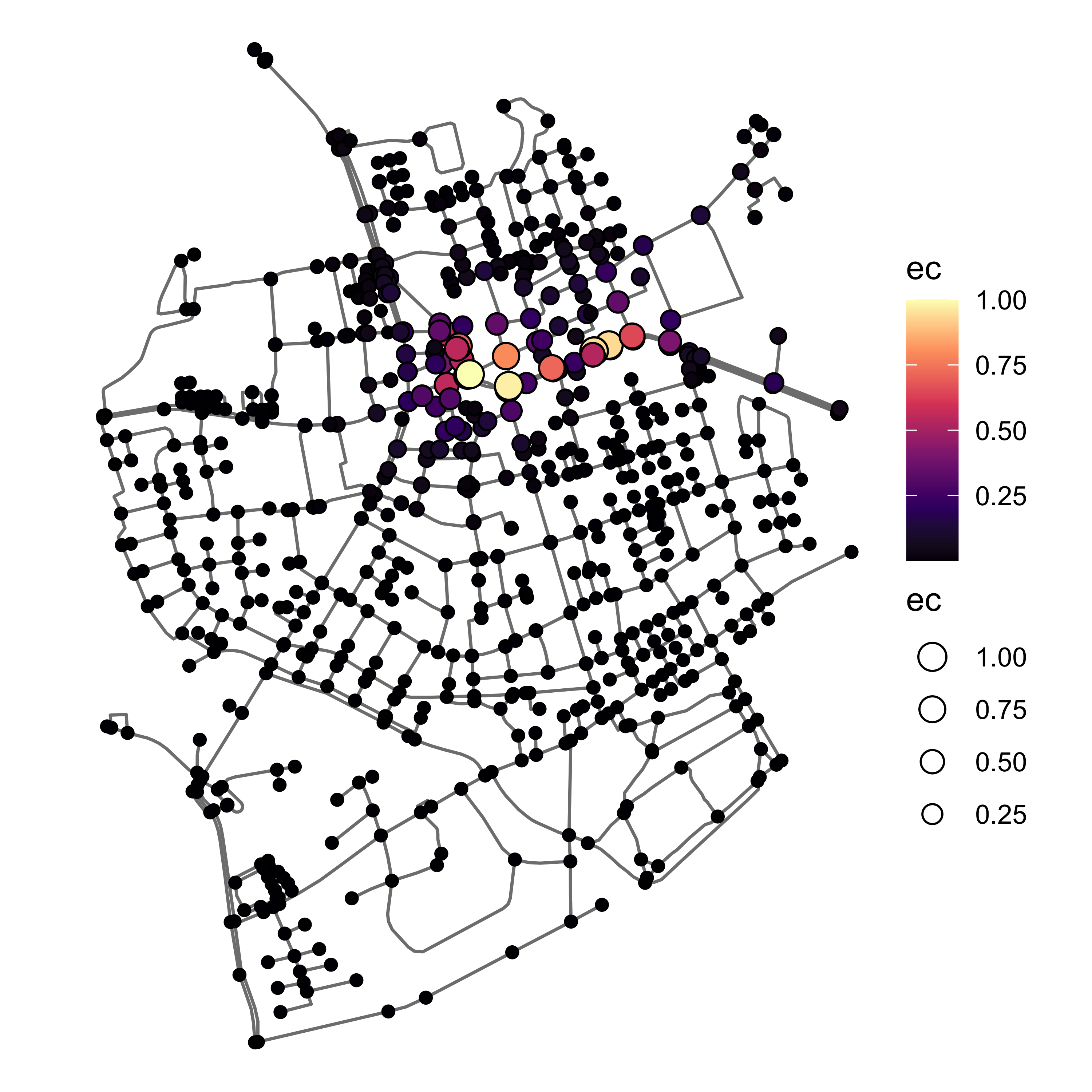
Центральность по влиятельности показывает сумму степеней вершин, с которыми связана текущая вершина.
Интерпретация
Центральность по влиятельности позволяет выделить области графа, в которых наблюдается сложная топология сети
