Цифровое моделирование рельефа и геоморфометрия

Основы геоинформатики: лекция 8

Самсонов Тимофей Евгеньевич

29 марта 2024 г.

Покрытие

Покрытие (Open Geospatial Consortium Inc. 2005)

Пространственный объект, который действует как функция, возвращающая значения

• в пределах своей области значений (атрибутивного домена);

• в пределах своей области определения (пространственного, временного или пространственно-временного домена);

для любой точки в системе координат покрытия.

Цифровая модель рельефа

Цифровая модель рельефа (ЦМР)

Покрытие, функция которого возвращает параметр(ы) рельефа земной поверхности.

Примеры

Высоты, углы наклона, экспозиции, направления стока, формы рельефа и их элементы

Цифровая модель высот (ЦМВ)

Покрытие, функция которого возвращает отметку высоты земной поверхности.

Заменяемость терминов

Обычно, когда говорят о ЦМР, предполагают в виду именно ЦМВ, т.к. это наиболее распространенный случай. Ошибкой это не считается.

Растровая ЦМР

Наиболее часто для представления ЦМР используются растровые покрытия.

В качестве функции покрытия используется билинейная, бикубическая и прочие методы интерполяции.

Справа изображен фрагмент растровой ЦМР. Окрестность \(3 \times 3\).

Растровая ЦМР — пример

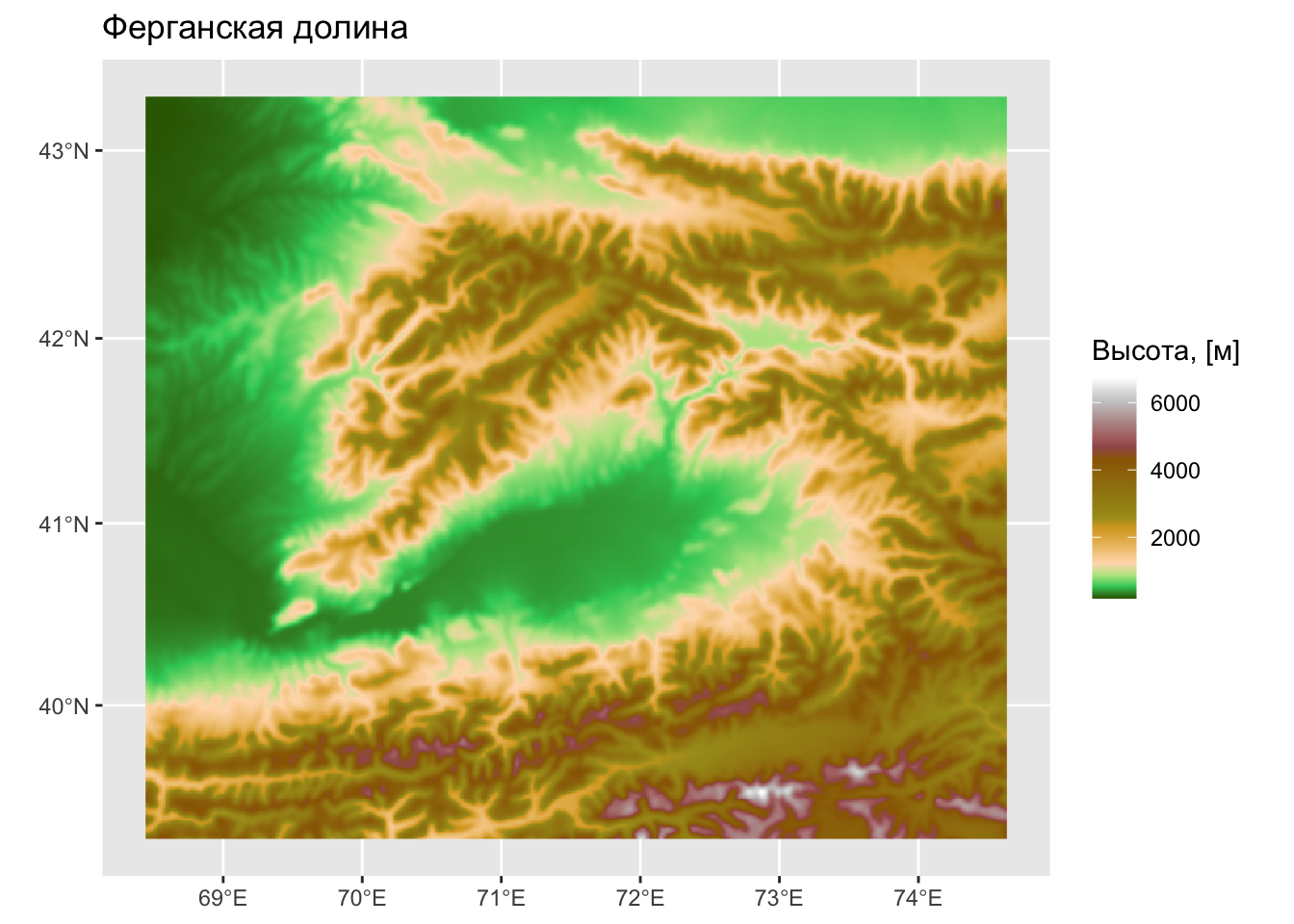
Растровая ЦМР — крупно

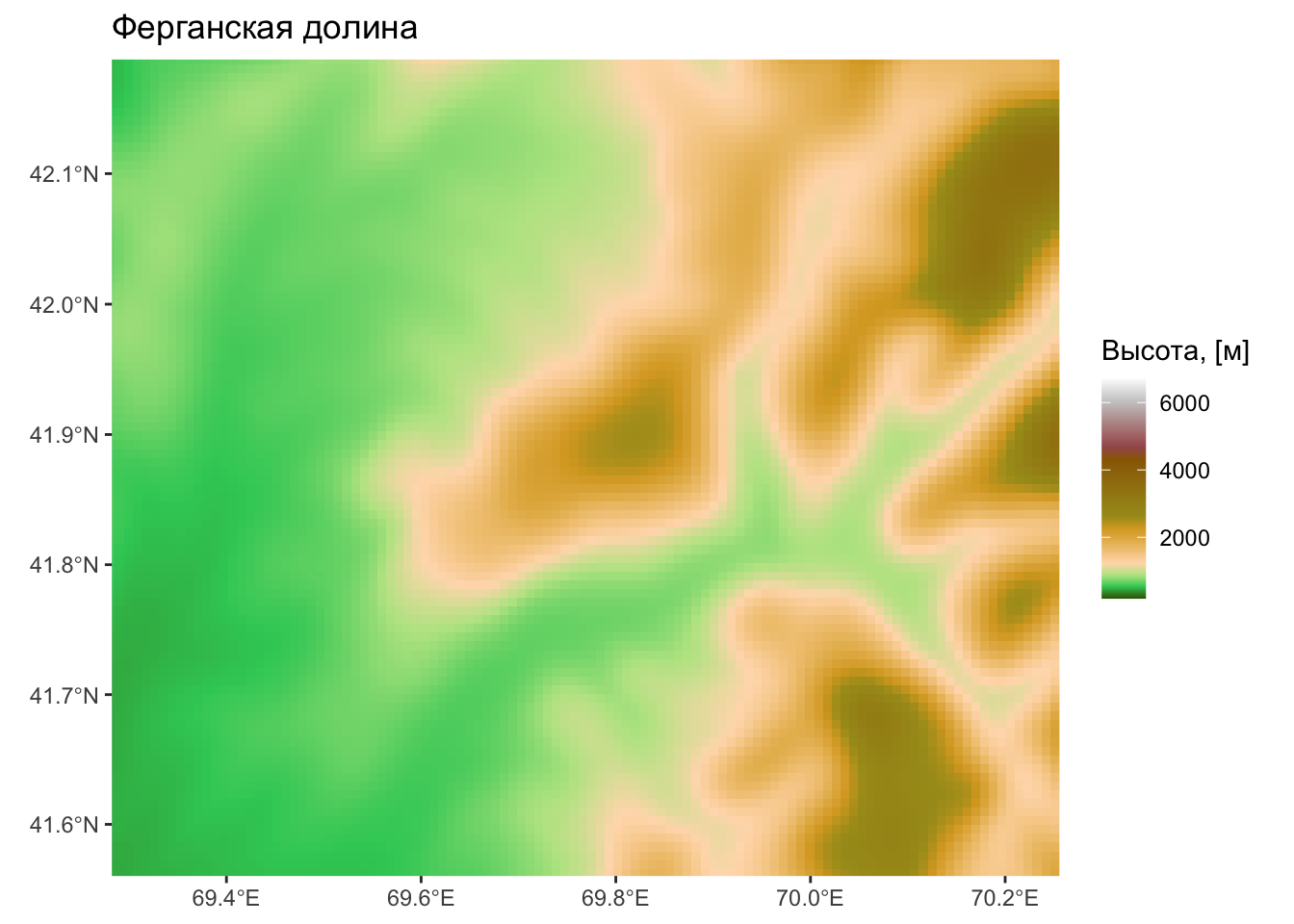
Геоморфометрия

Геоморфометрия — геометрический анализ земной поверхности.

Распространенные задачи геоморфометрии включают:

1. Вычисление локальных морфометрических величин.
2. Выделение форм и элементов форм рельефа.
3. Гидрологический и топоклиматический анализ.

Для представления поверхности как правило используется ЦМР.

Применение

Методы геоморфометрии могут применяться к рельефу любой поверхности, не только земной. Например, градиент (скорость изменения) может быть вычислен как для отметок высот, так и для температур.

Аппроксимация поверхности

Для вычисления производных поверхность локально аппроксимируется.

Например, в методе Эванса (Evans 1980) используется функция 2 степени:

\[ Z(x,y) = \\ Ax^2 + By^2 + Cxy + Dx +Ey + F \]

Узлов больше чем коэффициентов

Поэтому поверхность не проходит через узлы, а даёт общий тренд. Устойчивость к случайным ошибкам в данных повышается.

Производные поверхности

Производные поверхности имеют важнейшее значение для анализа рельефа:

\[ \frac{\partial Z}{\partial x} = 2Ax + Cy + D \rightarrow Z_x \\ \frac{\partial Z}{\partial y} = 2By + Cx + E \rightarrow Z_y \]

При вычислении в центральном узле окрестности:

\[ Z_x (0,0) = D; \ \ Z_y (0,0) = E \]

Морфометрические величины

Морфометрические величины, рассчитываемые для узла сетки называются локальными.

Уклон (\(S\)) и угол наклона (\(\phi\)):

\[ S = \sqrt{Z_x^2 + Z_y^2}; \ \phi = \arctan(S) \]

Экспозиция:

\[ \theta = \pi - \arctan \Big(\frac{Z_y}{Z_x}\Big) + \frac{\pi}{2} \Big(\frac{Z_x}{|Z_x|}\Big) \]

Углы наклона

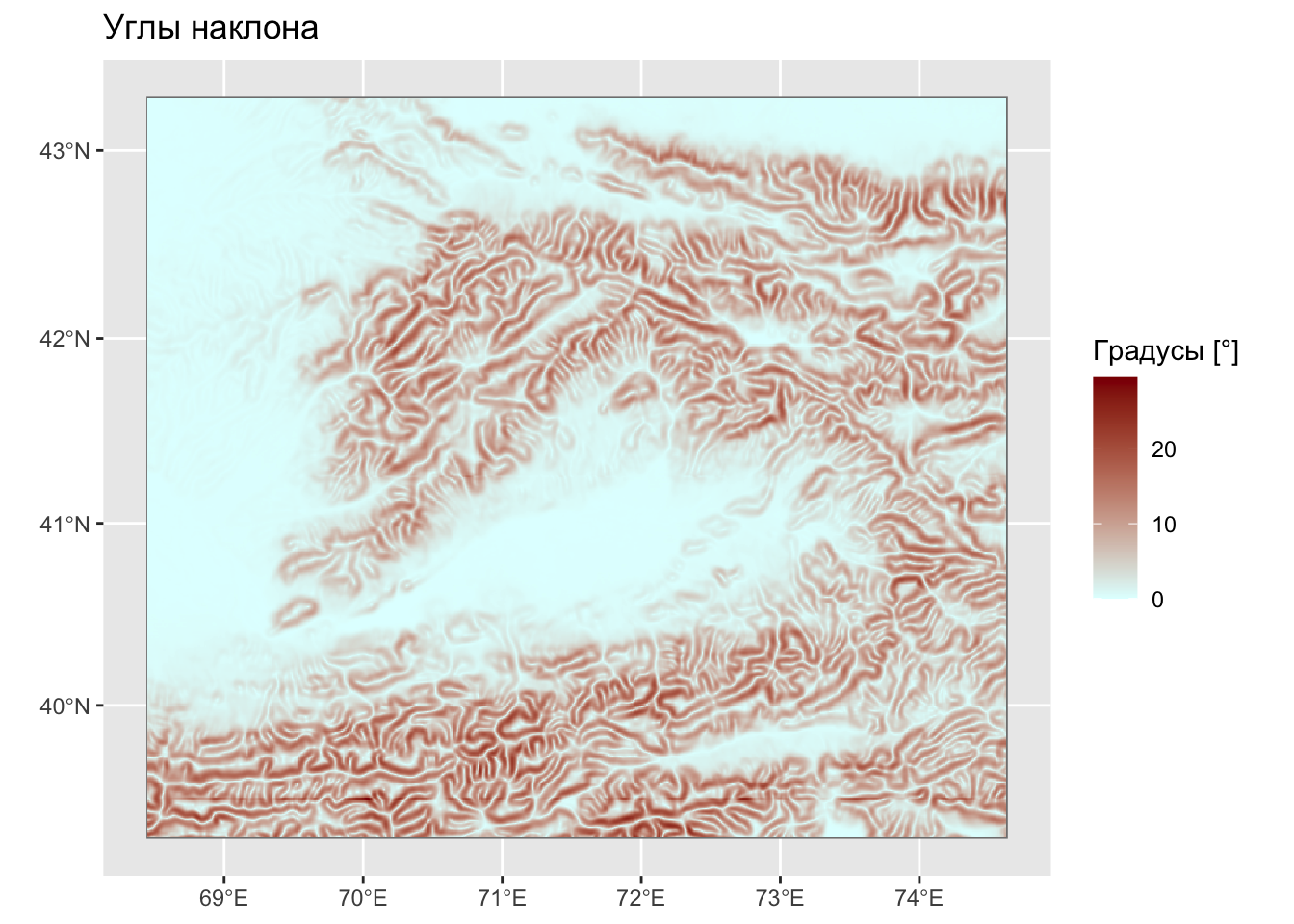
Углы наклона — крупно

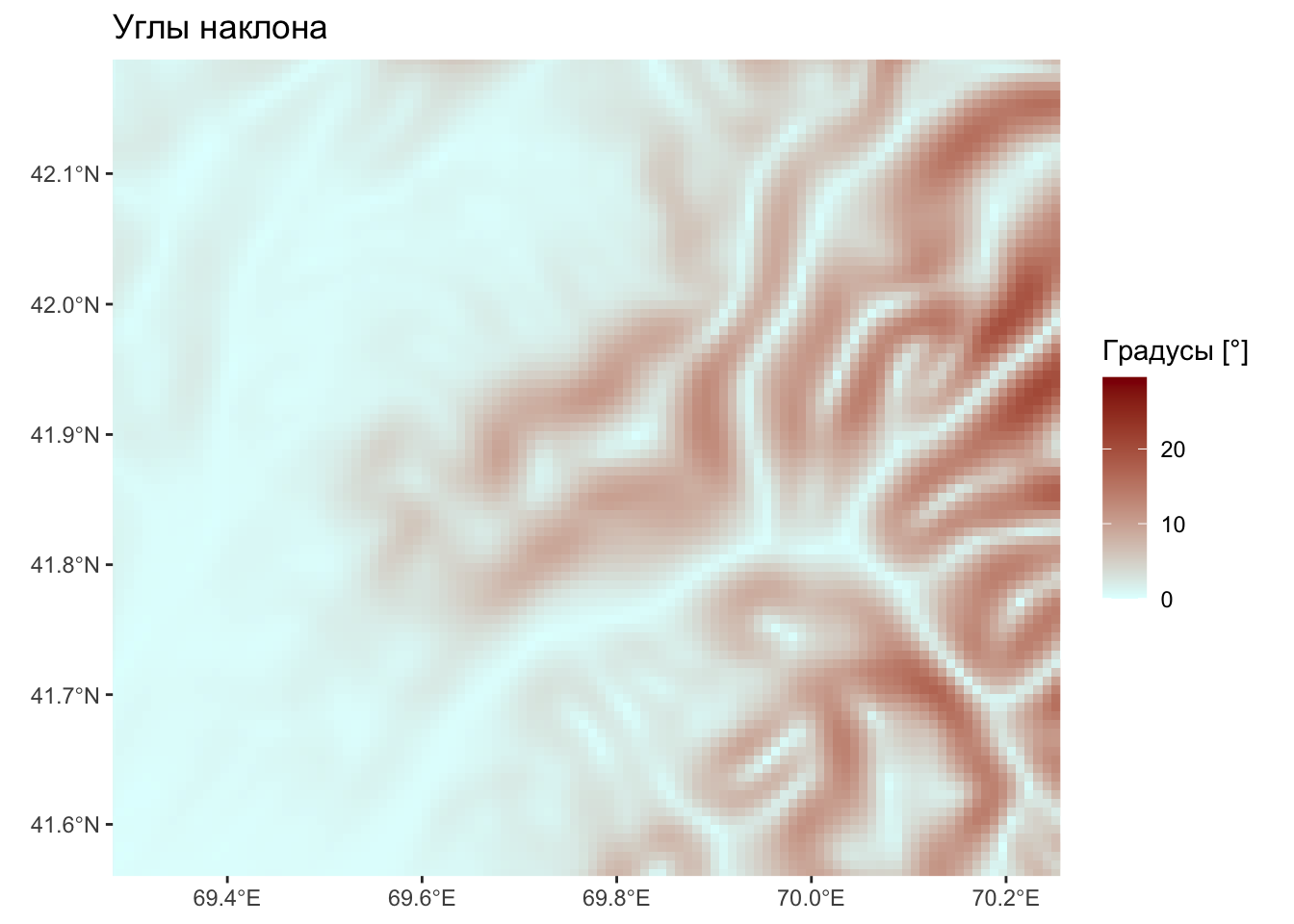
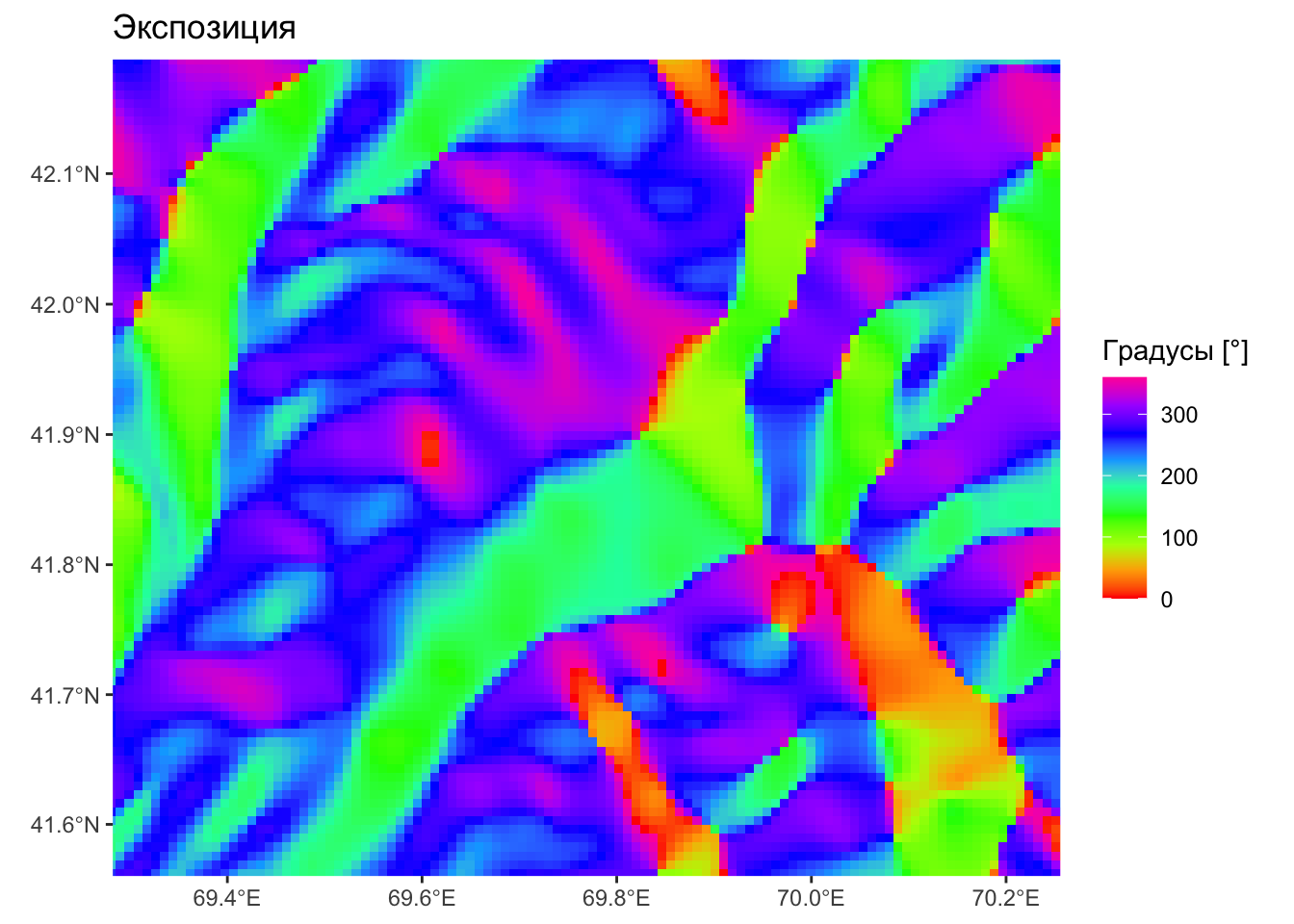
Экспозиция

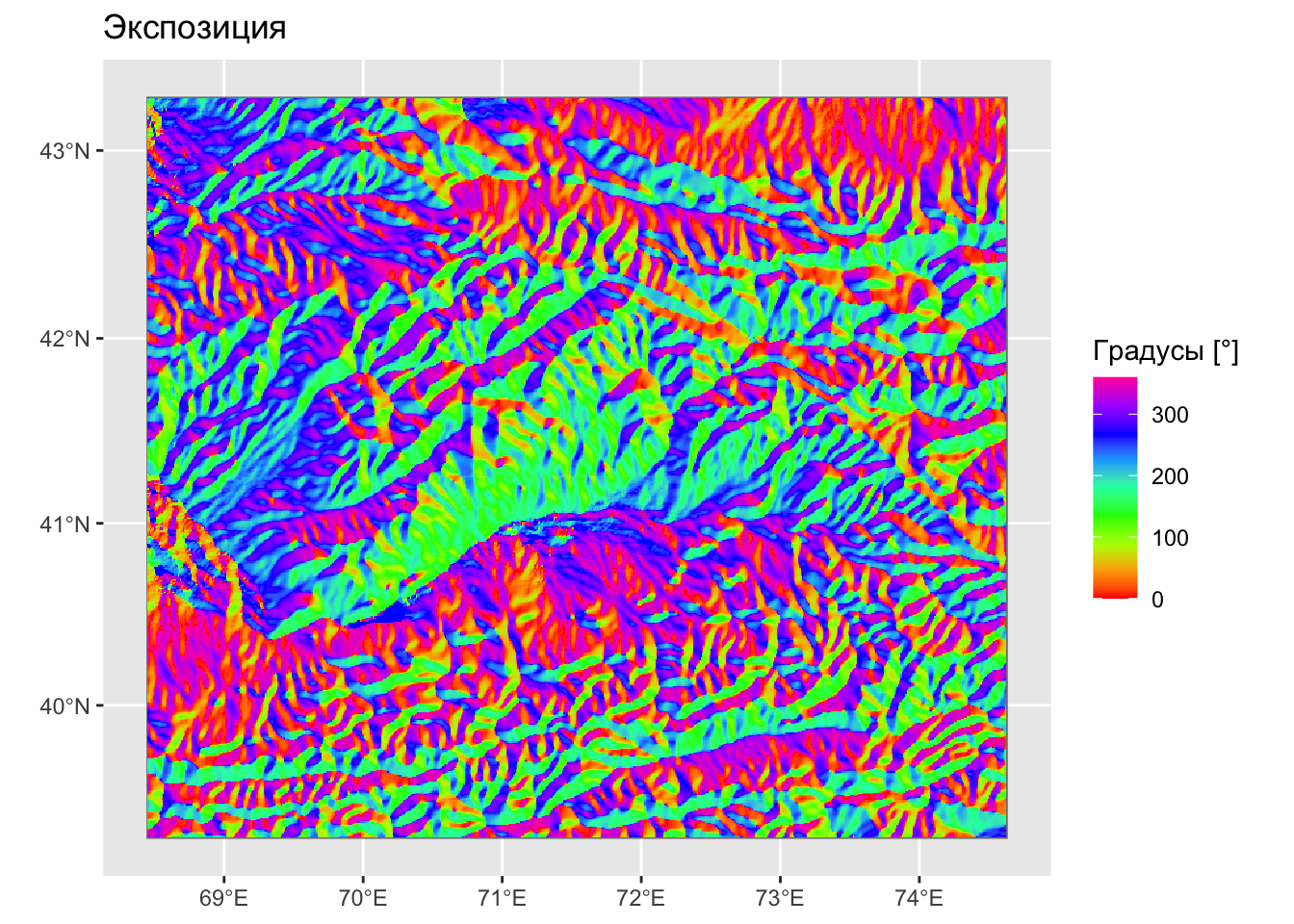
Экспозиция — крупно

Морфометрические величины

Кривизна кривой обратно пропорциональна радиусу касательной окружности \(r\) — радиусу кривизны.

• чем больше радиус, тем меньше кривизна;

• выпуклые и вогнутые изгибы различаются знаком кривизны;

• единица измерения кривизны обычно \(1/м\).

Морфометрические величины

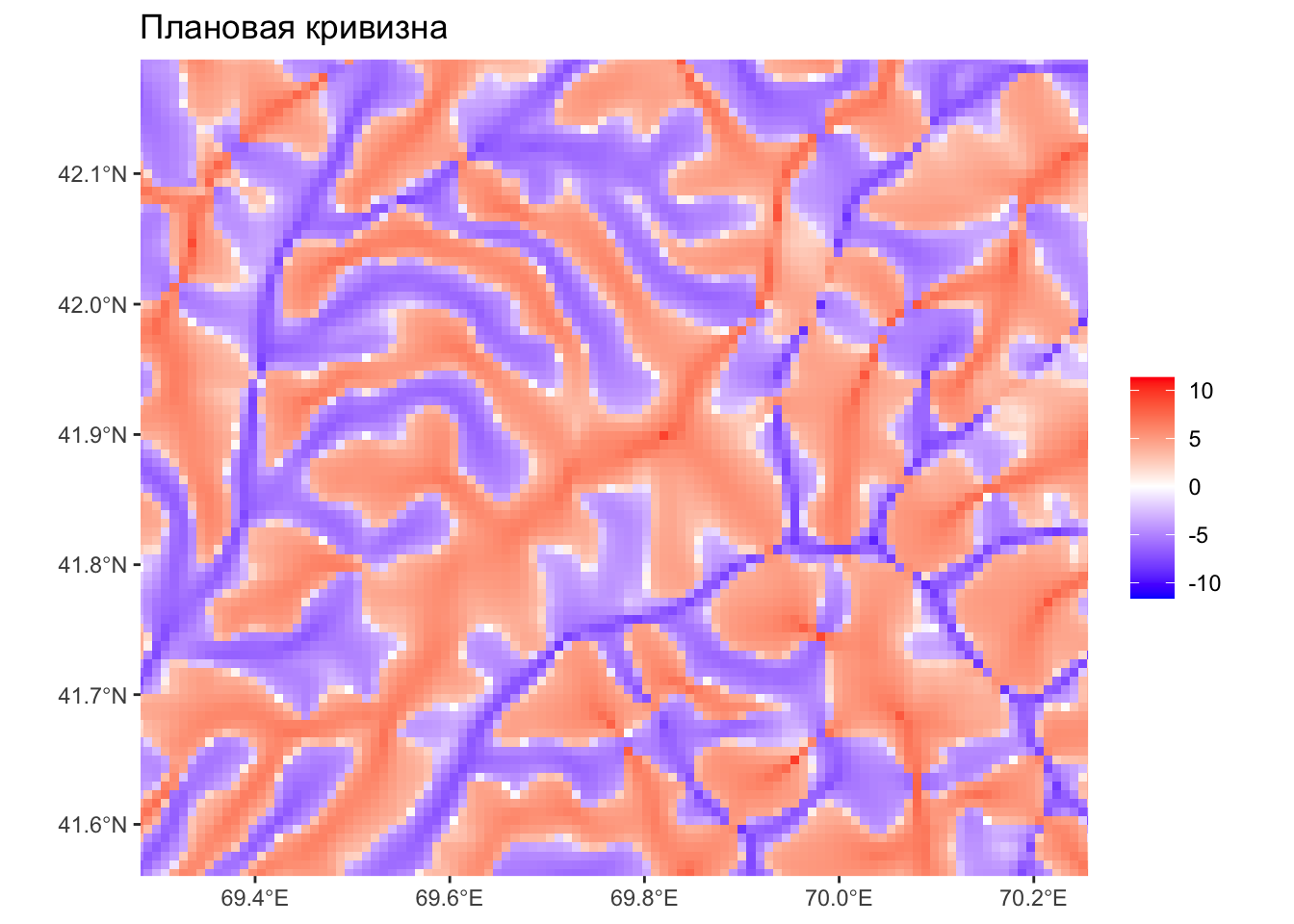
Плановая кривизна:

\[ K_{p} = \frac{Z_{xx} \color{red}{Z_x^2 +} 2Z_{xy} Z_x Z_y + Z_{yy} \color{red}{Z_y^2} }{pq^{3/2}} \]

Интерпретация

Кривизна изолинии поверхности в точке. Положительные значения соответствуют областям дивергенции (хребты), отрицательные — конвергенции (тальвеги).

Профильная кривизна:

\[ K_{c} = \frac{Z_{xx} \color{blue}{Z_y^2 -} 2Z_{xy} Z_x Z_y + Z_{yy} \color{blue}{Z_x^2} }{pq^{3/2}} \]

Интерпретация

Кривизна склона в направлении максимального уклона. Положительные значению соответствуют вогнутым склонам, отрицательные — выпуклым.

\(\frac{\partial^2 Z}{\partial x^2} = 2A \rightarrow Z_{xx}; \ \frac{\partial^2 Z}{\partial y^2} = 2B \rightarrow Z_{yy}; \ \frac{\partial^2 Z}{\partial x \partial y} = C \rightarrow Z_{xy}\)

\(p = Z_x^2 + Z_y^2; \ q = p + 1\)

Плановая кривизна

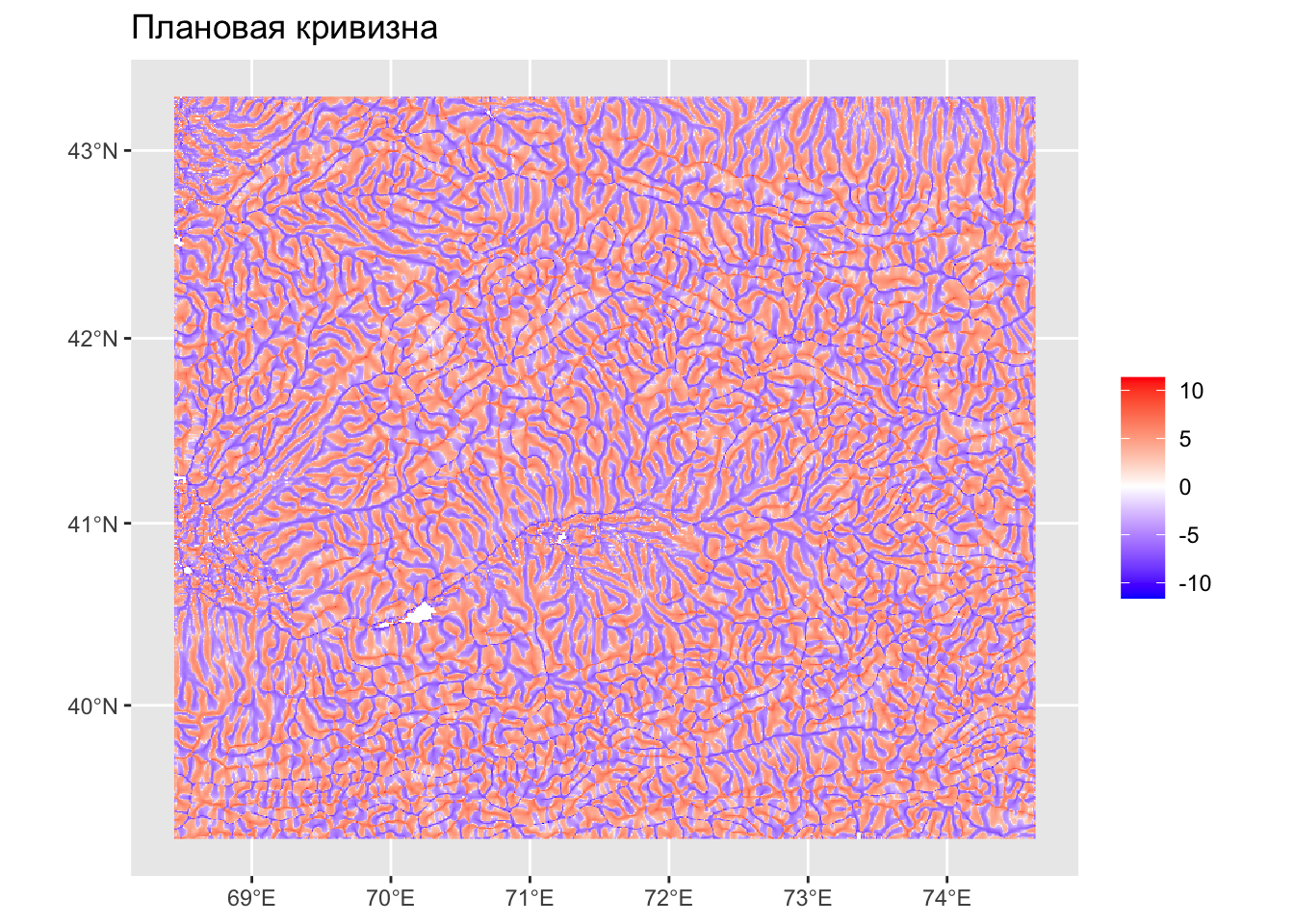
Плановая кривизна — крупно

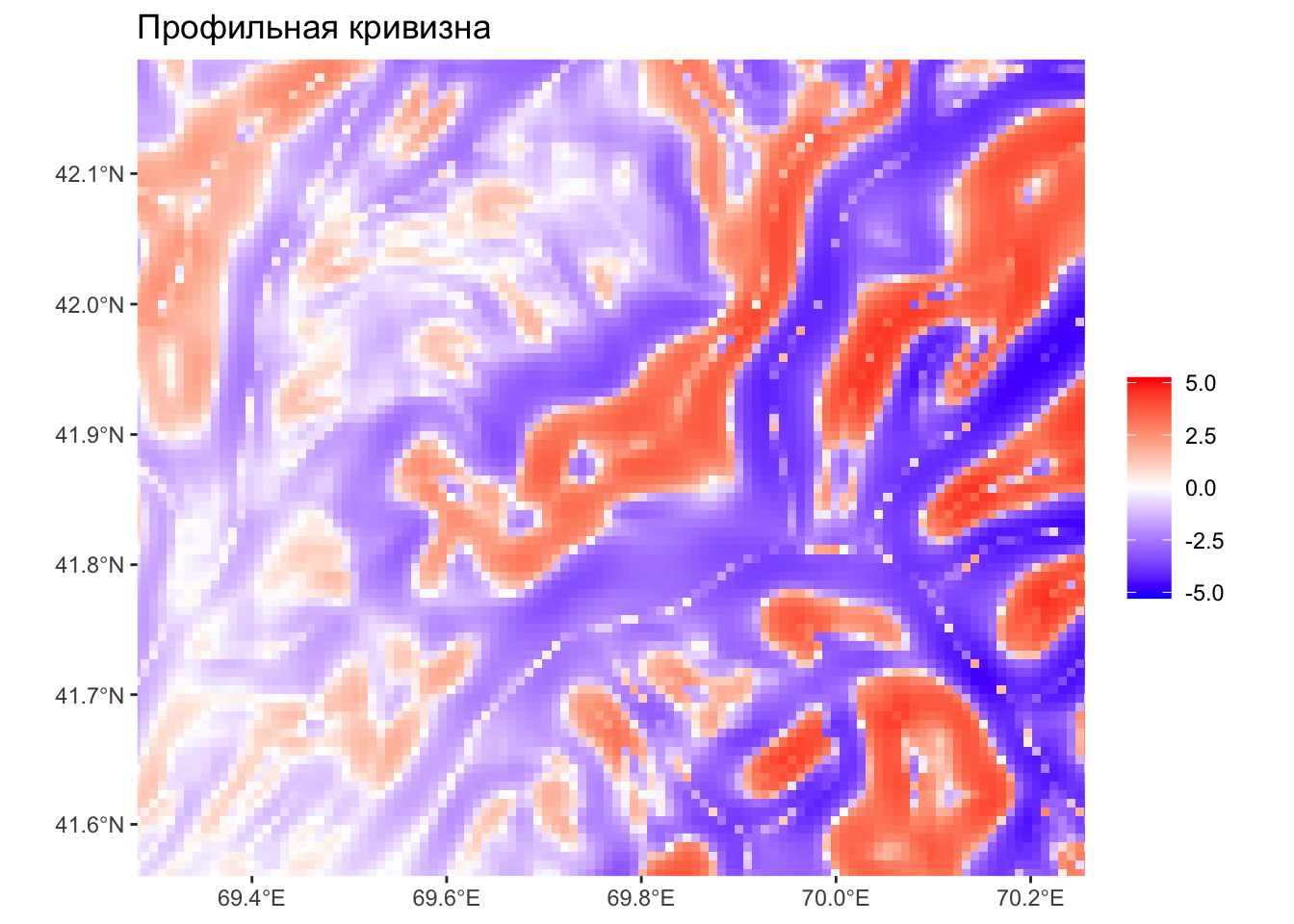
Профильная кривизна

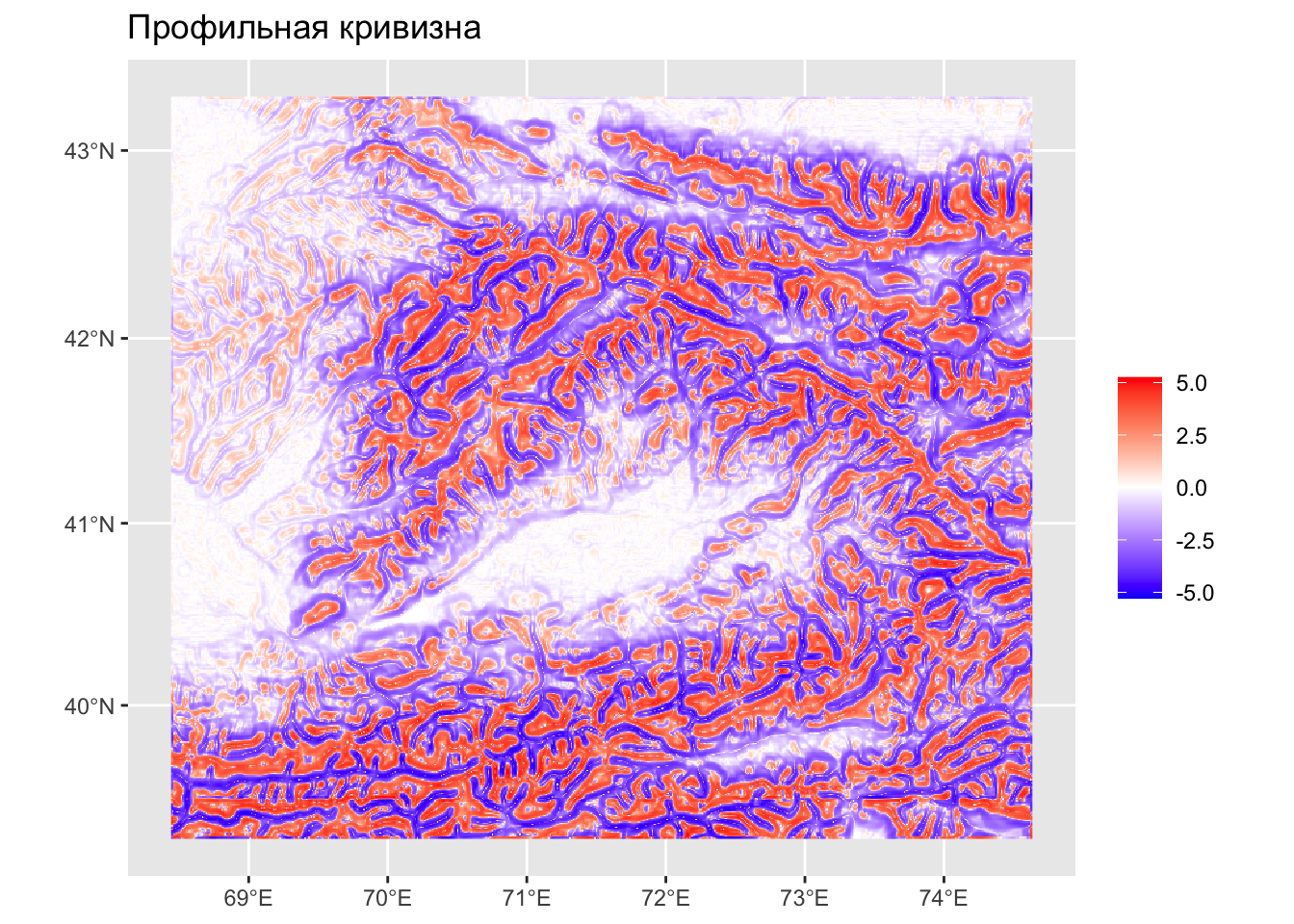
Профильная кривизна — крупно

Интенсивность отражения света

В модели Ламберта зависит от угла \(\alpha\) между вектором нормали к поверхности \(\textbf N\) и вектором направления на источник света \(\textbf L\):

\[ I = \cos \alpha = (\textbf L, \textbf N) \]

\(\textbf N = \big\{-Z_x, -Z_y, 1 \big\} \bigg/ \sqrt{Z_x^2 + Z_y^2 + 1}\)

\(\textbf L = \begin{cases} \cos(h) \cos(A),\\ \cos(h) \sin(A),\\ \sin(h) \end{cases}\)

\((\textbf L, \textbf N)\) — скалярное произведение;

\(A, \ h\) — азимут и высота источника света (Солнца).

Аналитическая отмывка

Визуализация интенсивности отраженного света.

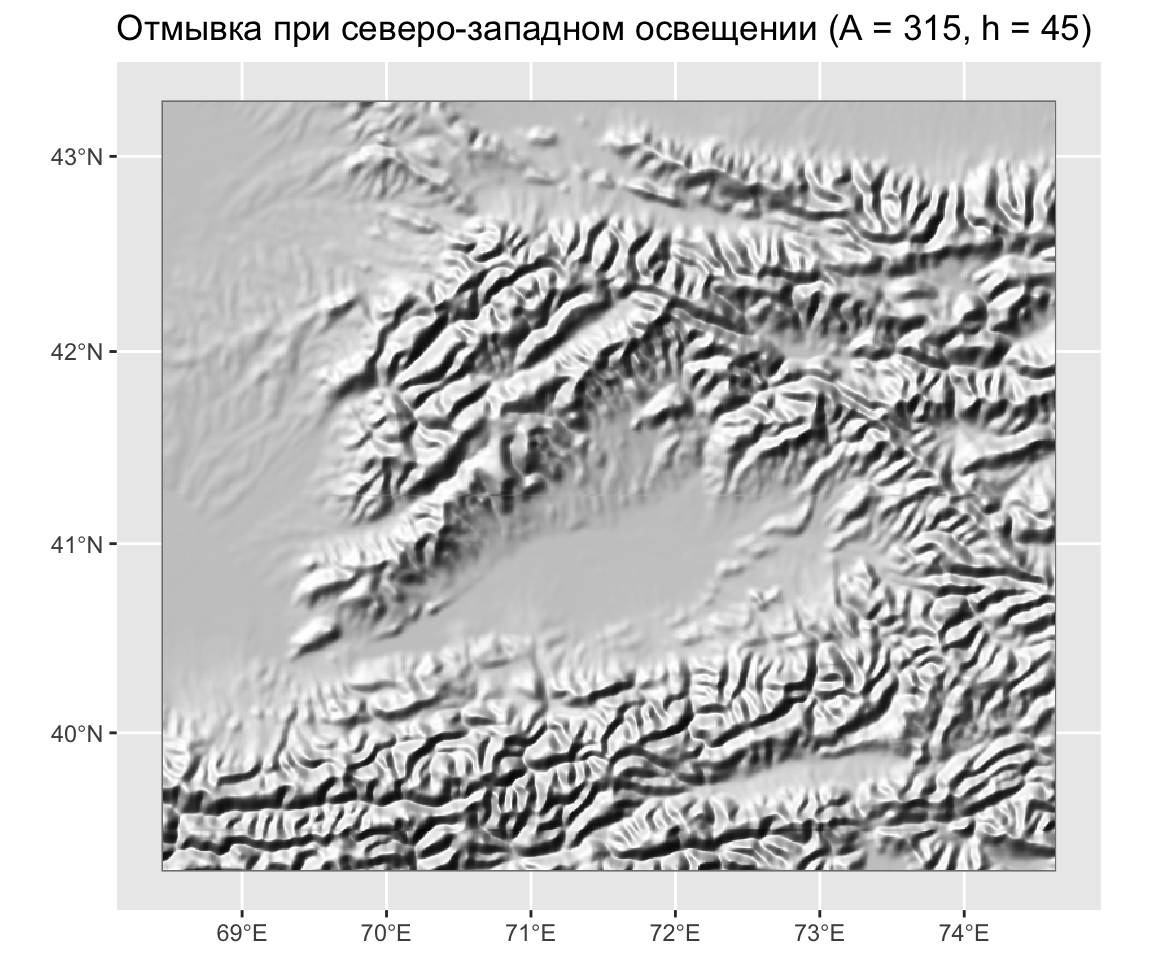
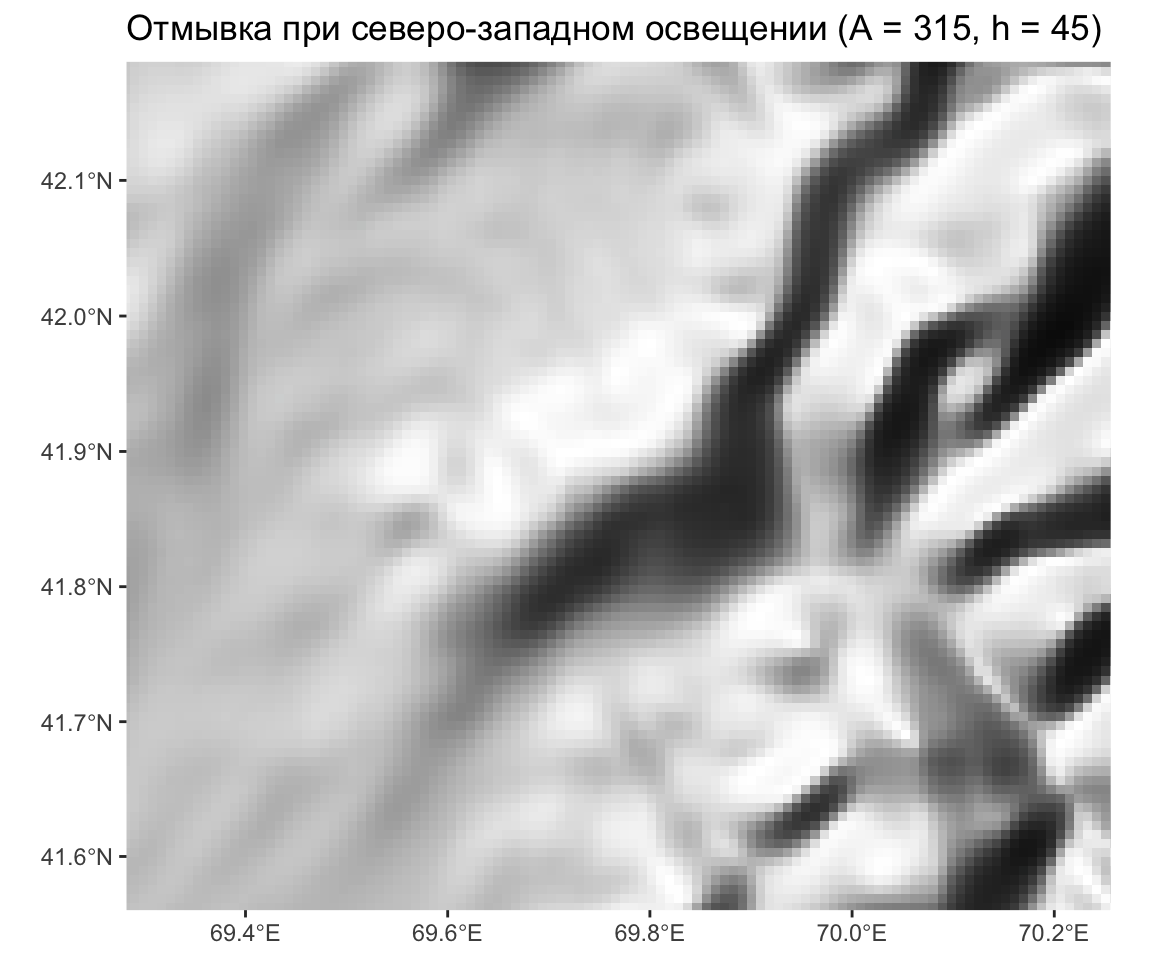
Аналитическая отмывка — крупно

Визуализация интенсивности отраженного света.

Отвесная отмывка

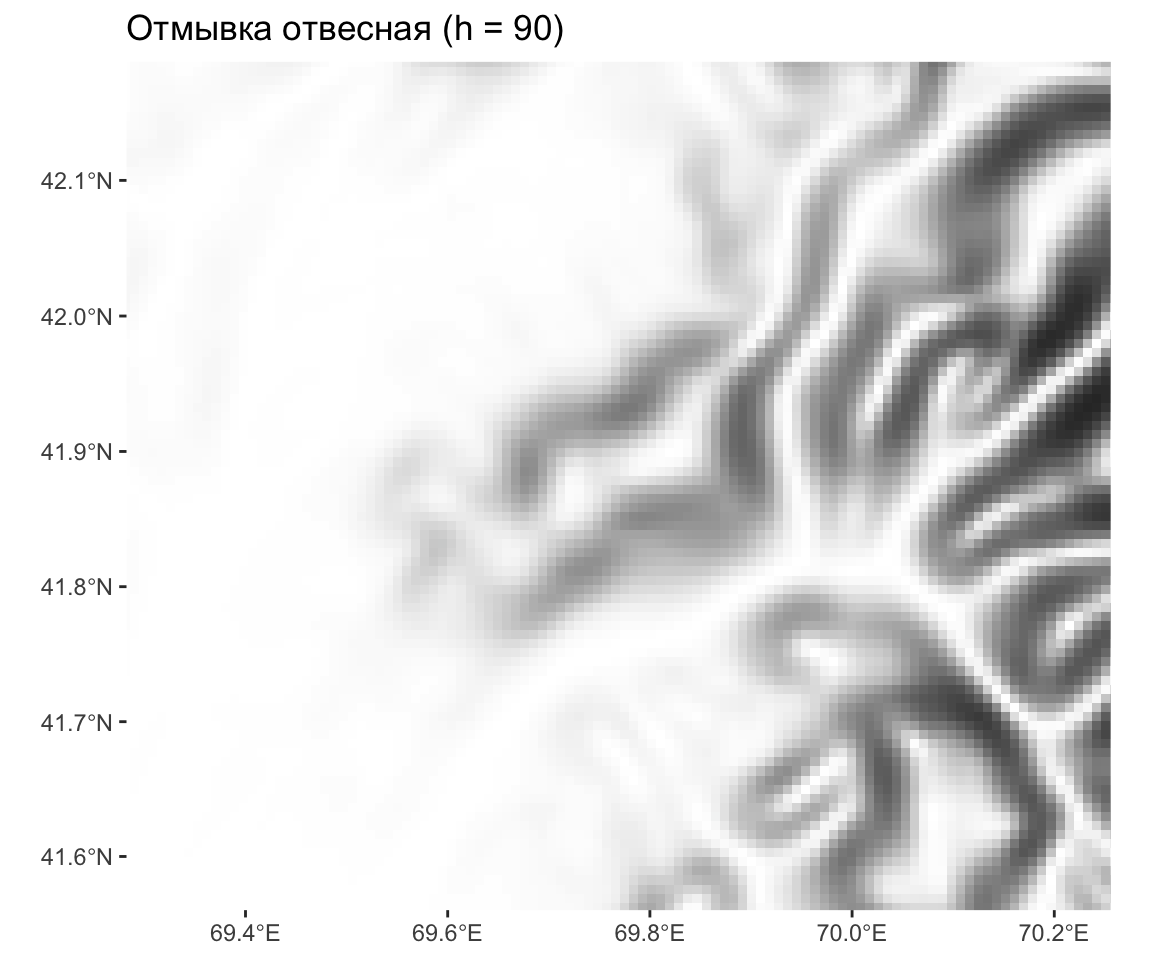
Отвесная отмывка подчеркивает линии хребтов.

Отвесная отмывка — крупно

Отвесная отмывка подчеркивает линии хребтов.

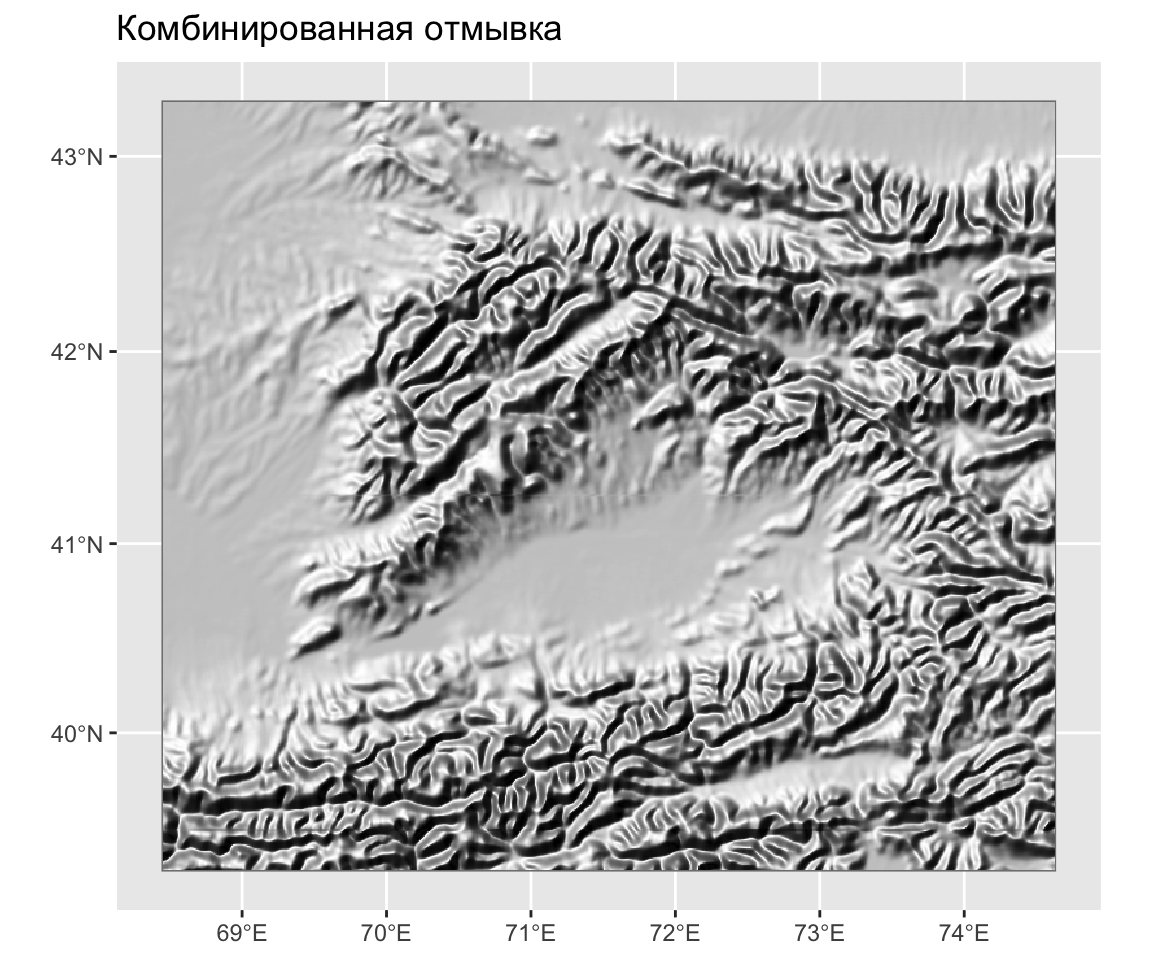
Комбинированная отмывка

Наиболее наглядна комбинация боковой и отвесной отмывки.

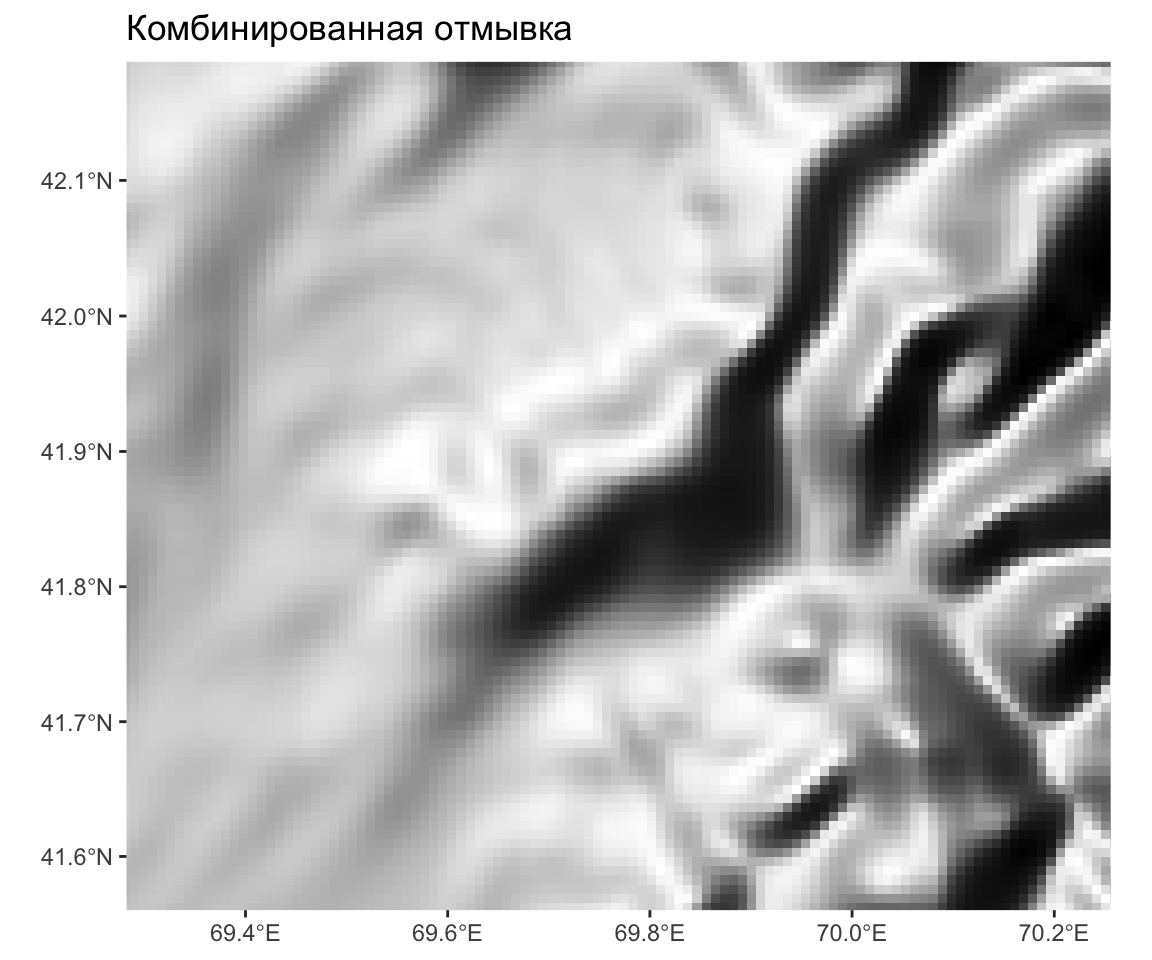
Комб. отмывка — крупно

Наиболее наглядна комбинация боковой и отвесной отмывки.

Гидрологический анализ ЦМР

Гидрологический анализ ЦМР — совокупность методов обработки ЦМР, связанных с анализом и моделированием геометрических условий распределения поверхностного стока.

Распространенные задачи гидрологического анализа включают:

1. Определение направлений стока.
2. Вычисление площади водосбора.
3. Построение сети потенциальных водотоков.
4. Построение границ бассейнов.

Предварительная подготовка ЦМР

Для гидрологического анализа играют очень важную роль процедуры предварительной подготовки ЦМР, такие как устранение ошибочных замкнутых локальных понижений.

Ошибочные локальные понижения

Почти всегда присутствуют в ЦМР из-за неточности алгоритмов ее построения. Являются “ловушками” для стока.

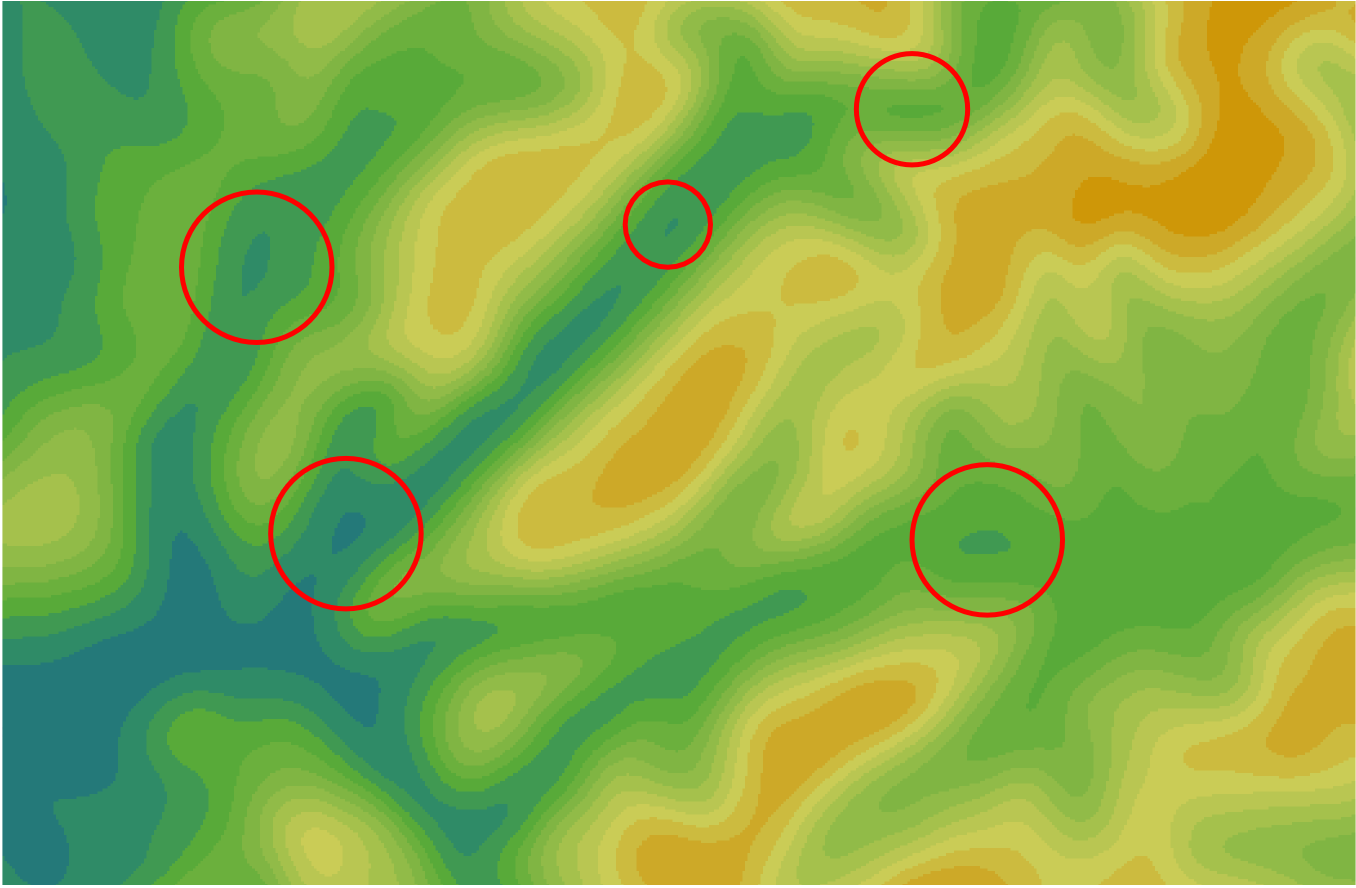
Ошибочные локальные понижения

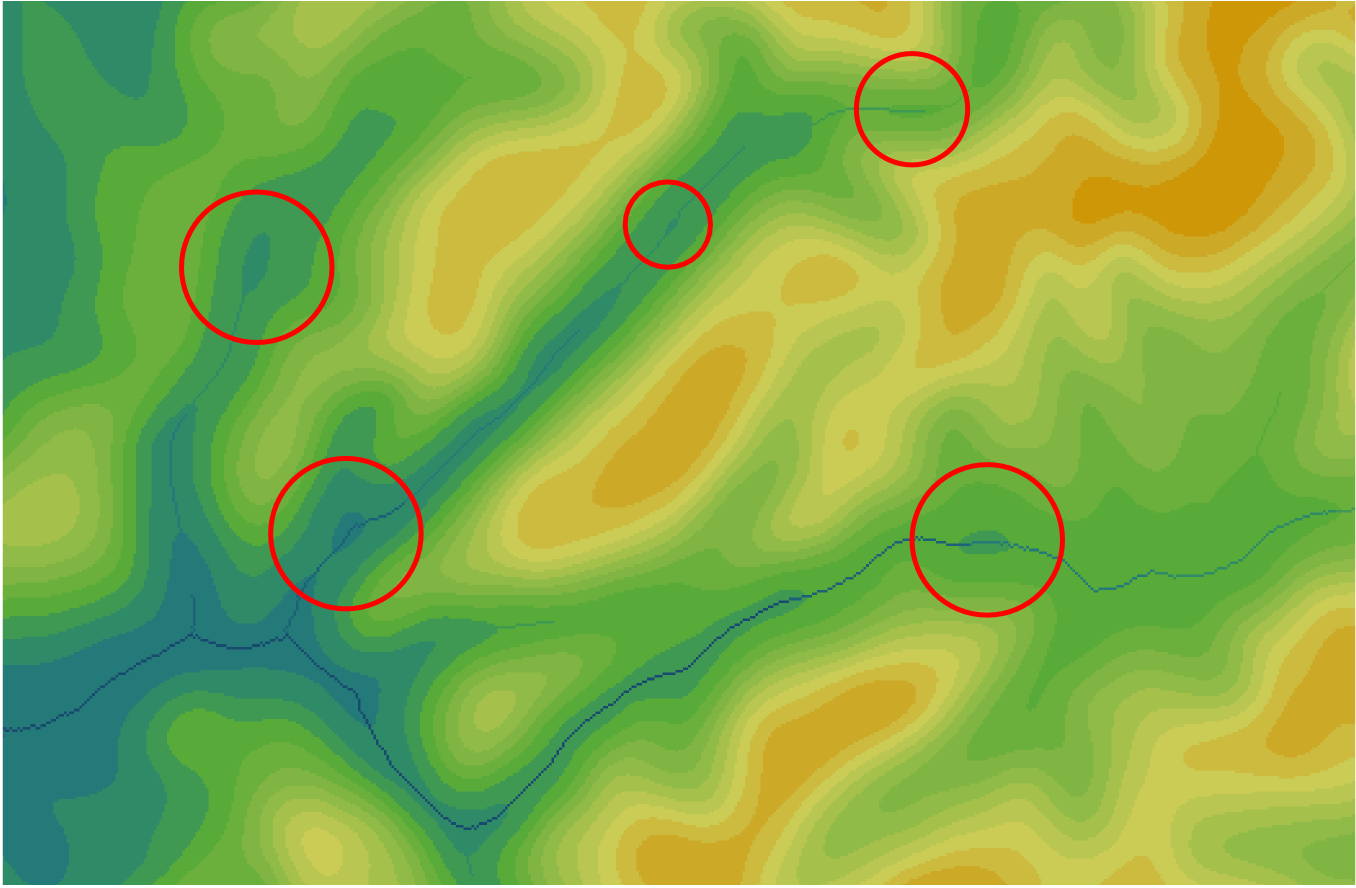
Для гидрологического моделирования важно такие понижения устранить. Чаще всего их заполняют (Fill Sinks) как на рисунке.

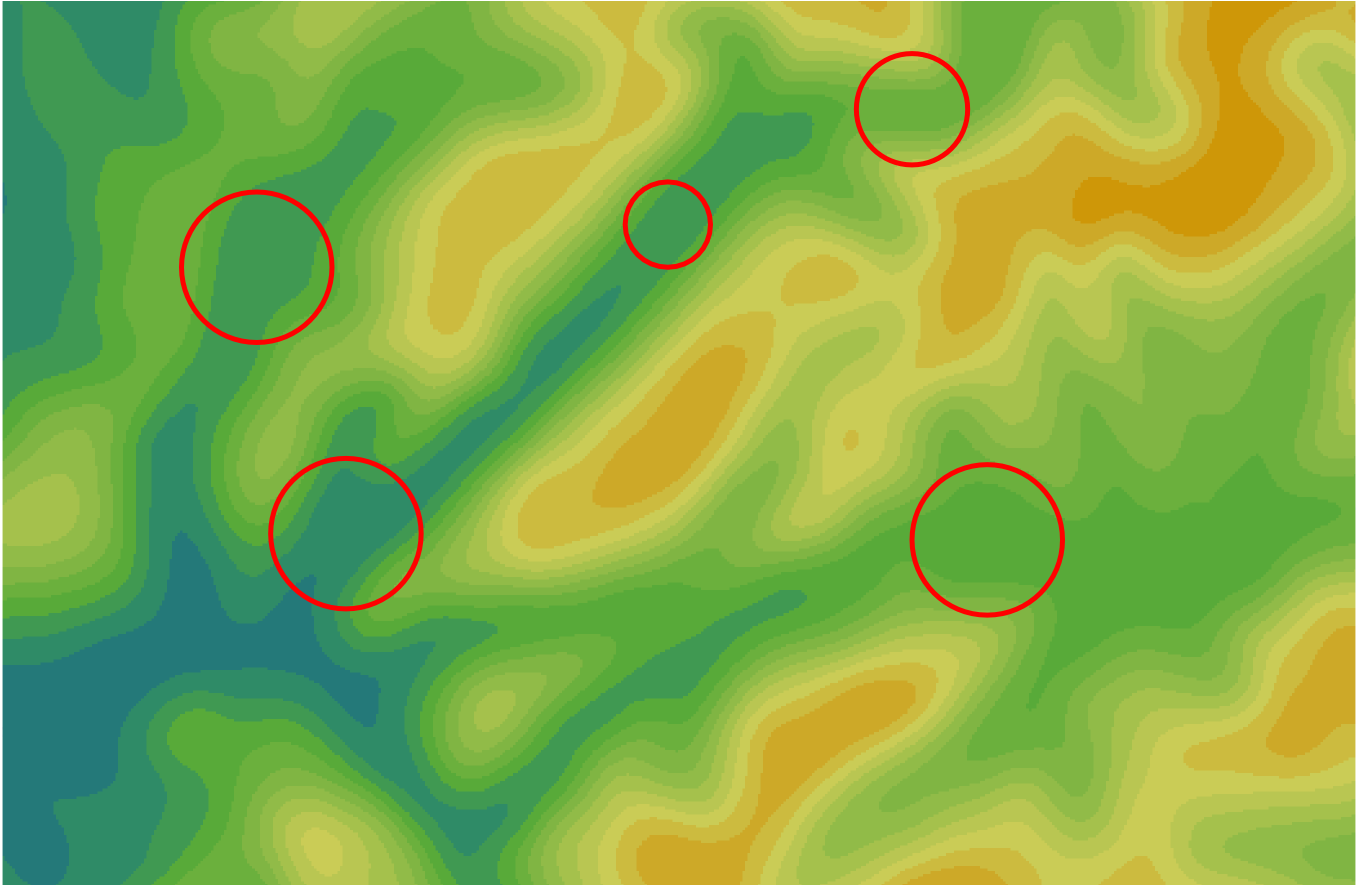
Ошибочные локальные понижения

Более сложные алгоритмы выполняют прорыв (carving, breaching) понижений путем прорезания кратчайших путей между ними.

Направление стока

Направление стока указывает распределение стока по одному или множеству направлений.

В методе D8 (O’Callaghan и Mark 1984) весь сток направляется в направлении ячейки с максимальным уклоном.

• Направления кодируются числами вида \(2^n\).

• Код 0 используется для бессточных ячеек.

• Направление стока строго однозначно.

Метод D8

Алгоритм вычисления

Цифровая модель высот

Метод D8

Алгоритм вычисления

1. Получить разности высот соседних ячеек и центральной ячейки

Разности высот

Метод D8

Алгоритм вычисления

1. Получить разности высот соседних ячеек и центральной ячейки

2. Разности диагональных соседей поделить на \(\sqrt{2}\), т.к. их центры соответственно дальше.

Скорректированные разности высот

Метод D8

Алгоритм вычисления

1. Получить разности высот соседних ячеек и центральной ячейки

2. Разности диагональных соседей поделить на \(\sqrt{2}\), т.к. их центры соответственно дальше.

3. Среди полученных разностей найти минимальную.

Ячейка с минимальной разностью

Метод D8

Алгоритм вычисления

1. Получить разности высот соседних ячеек и центральной ячейки

2. Разности диагональных соседей поделить на \(\sqrt{2}\), т.к. их центры соответственно дальше.

3. Среди полученных разностей найти минимальную.

4. Если она отрицательная, то присвоить соответствующий код направления.

Выполнить для всех ячеек ЦМР.

Код направления D8

А если нет отрицательных?

Если все разности \(\geq 0\), то стока из ячейки нет. Будет присвоен код \(0\).

Метод D8

Особенности растра D8

• В каждой ячейке записан код направления стока.

• Код указывает куда из ячейки пойдет сток.

  Например, \(16\) означает “в юго-западном направлении” (если растр ориентирован по сторонам света).

• Коды не имеют количественной интерпретации, это условные обозначения направлений.

Пример растра направлений стока D8

Направление стока

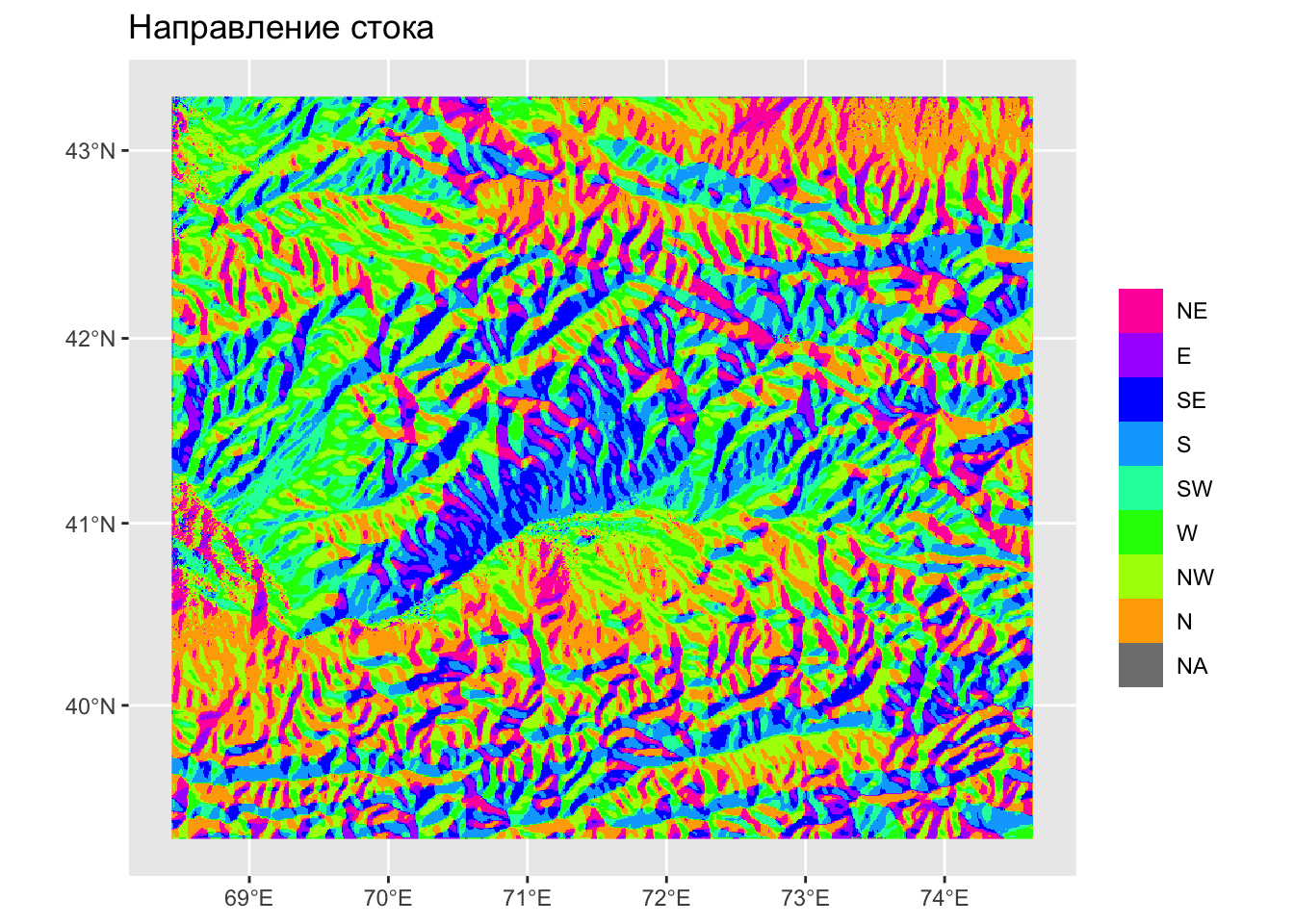
Направление стока — крупно

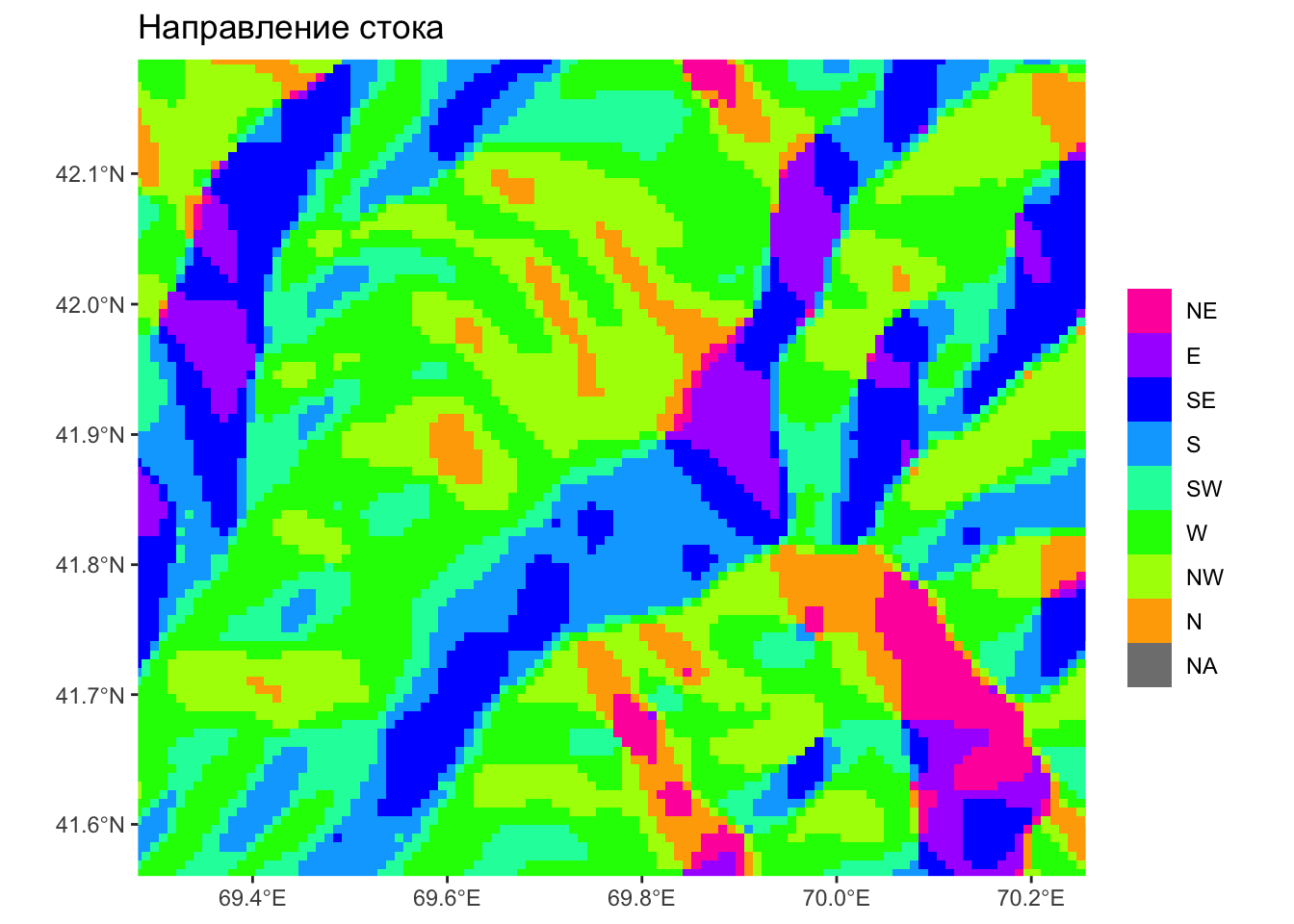
Аккумуляция стока

Аккумуляция стока — количественный показатель, аппроксимирующий площадь бассейна.

Может быть выражена в:

• количестве дренируемых ячеек — сток из которых попадает в данный пиксель;

• суммарной площади дренируемых ячеек.

• суммарной площади дренируемых ячеек, нормированной на их ширину перпендикулярно направлению стока.

Пример растра аккумуляции стока

Аккумуляция стока

Аккумуляция стока — количественный показатель, аппроксимирующий площадь бассейна.

Аккумуляция в \(j\)-й ячейке:

\[ A_j = k + \sum_{i=1}^k A_i, \]

• \(k\) — количество соседних ячеек, сток из которых попадает в \(j\)-ю;

• \(A_i\) — величина аккумуляции стока в \(i\)-й ячейке.

Пример растра аккумуляции стока

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.

Шаг 1

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.
2. Вычислить \(A_j = k + \sum_{i=1}^k A_i\) для всех ячеек, у которых \(A_i\) определено для всех входящих ячеек.

Шаг 2

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.
2. Вычислить \(A_j = k + \sum_{i=1}^k A_i\) для всех ячеек, у которых \(A_i\) определено для всех входящих ячеек.
3. Повторять шаг 2 до тех пор, пока \(A_j\) не будет известно для всех ячеек ЦМР.

Шаг 3

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.
2. Вычислить \(A_j = k + \sum_{i=1}^k A_i\) для всех ячеек, у которых \(A_i\) определено для всех входящих ячеек.
3. Повторять шаг 2 до тех пор, пока \(A_j\) не будет известно для всех ячеек ЦМР.

Шаг 4

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.
2. Вычислить \(A_j = k + \sum_{i=1}^k A_i\) для всех ячеек, у которых \(A_i\) определено для всех входящих ячеек.
3. Повторять шаг 2 до тех пор, пока \(A_j\) не будет известно для всех ячеек ЦМР.

Шаг 5

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.
2. Вычислить \(A_j = k + \sum_{i=1}^k A_i\) для всех ячеек, у которых \(A_i\) определено для всех входящих ячеек.
3. Повторять шаг 2 до тех пор, пока \(A_j\) не будет известно для всех ячеек ЦМР.

Шаг 6

Аккумуляция стока

Алгоритм вычисления:

1. Записать \(A_j=0\) во все ячейки, не имеющие входящего стока.
2. Вычислить \(A_j = k + \sum_{i=1}^k A_i\) для всех ячеек, у которых \(A_i\) определено для всех входящих ячеек.
3. Повторять шаг 2 до тех пор, пока \(A_j\) не будет известно для всех ячеек ЦМР.

Шаг 7

Аккумуляция стока

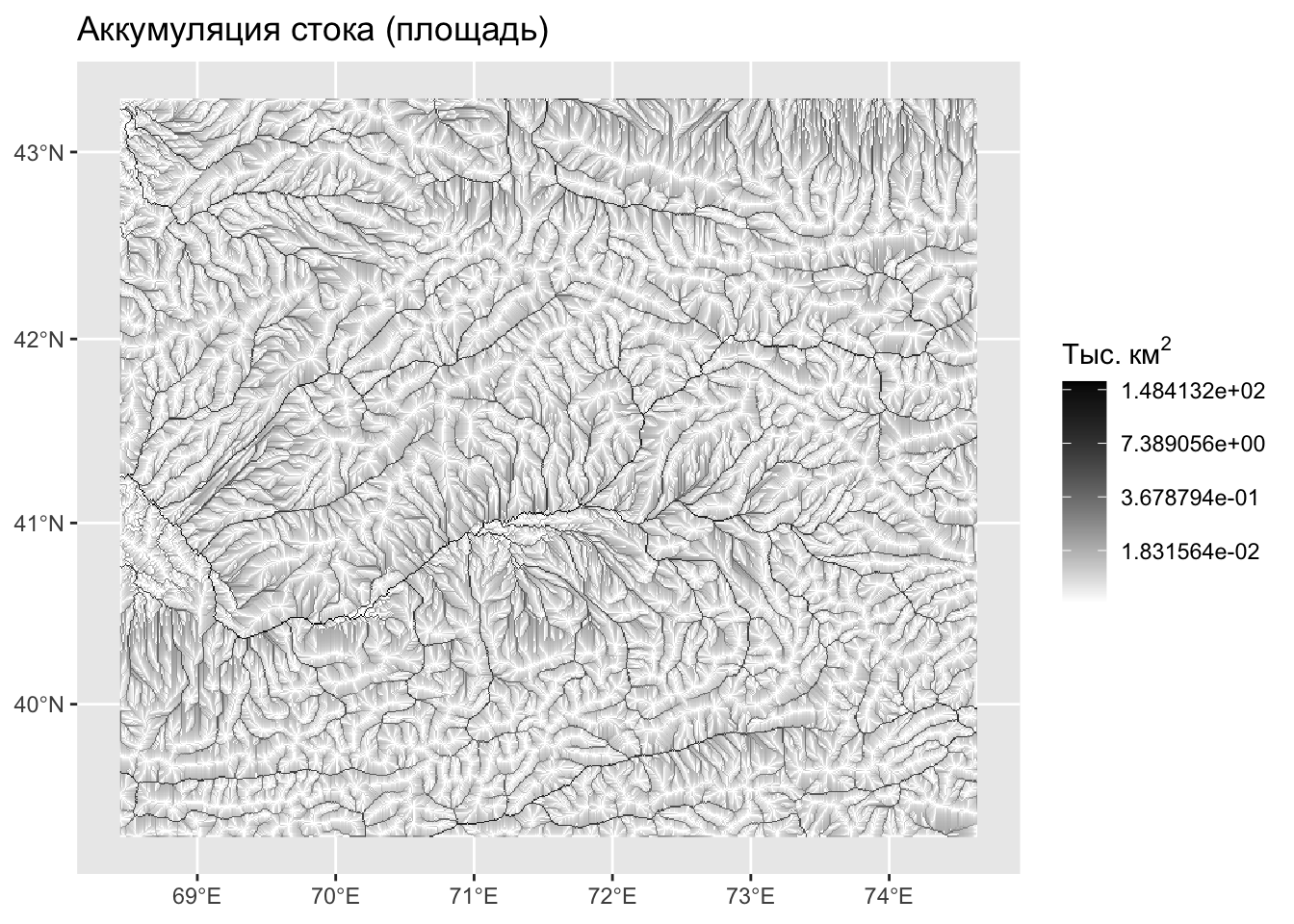
Аккумуляция стока — крупно

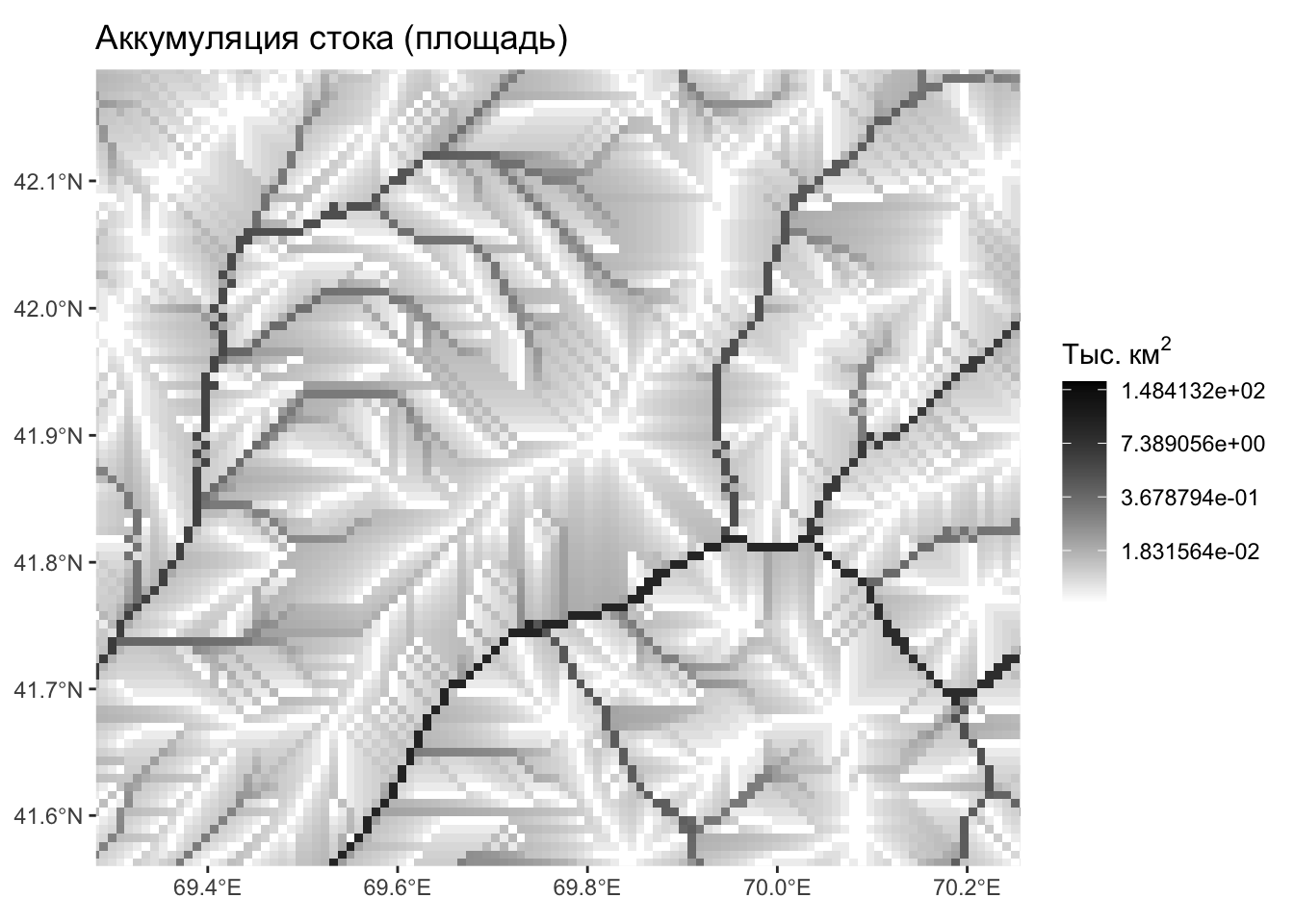
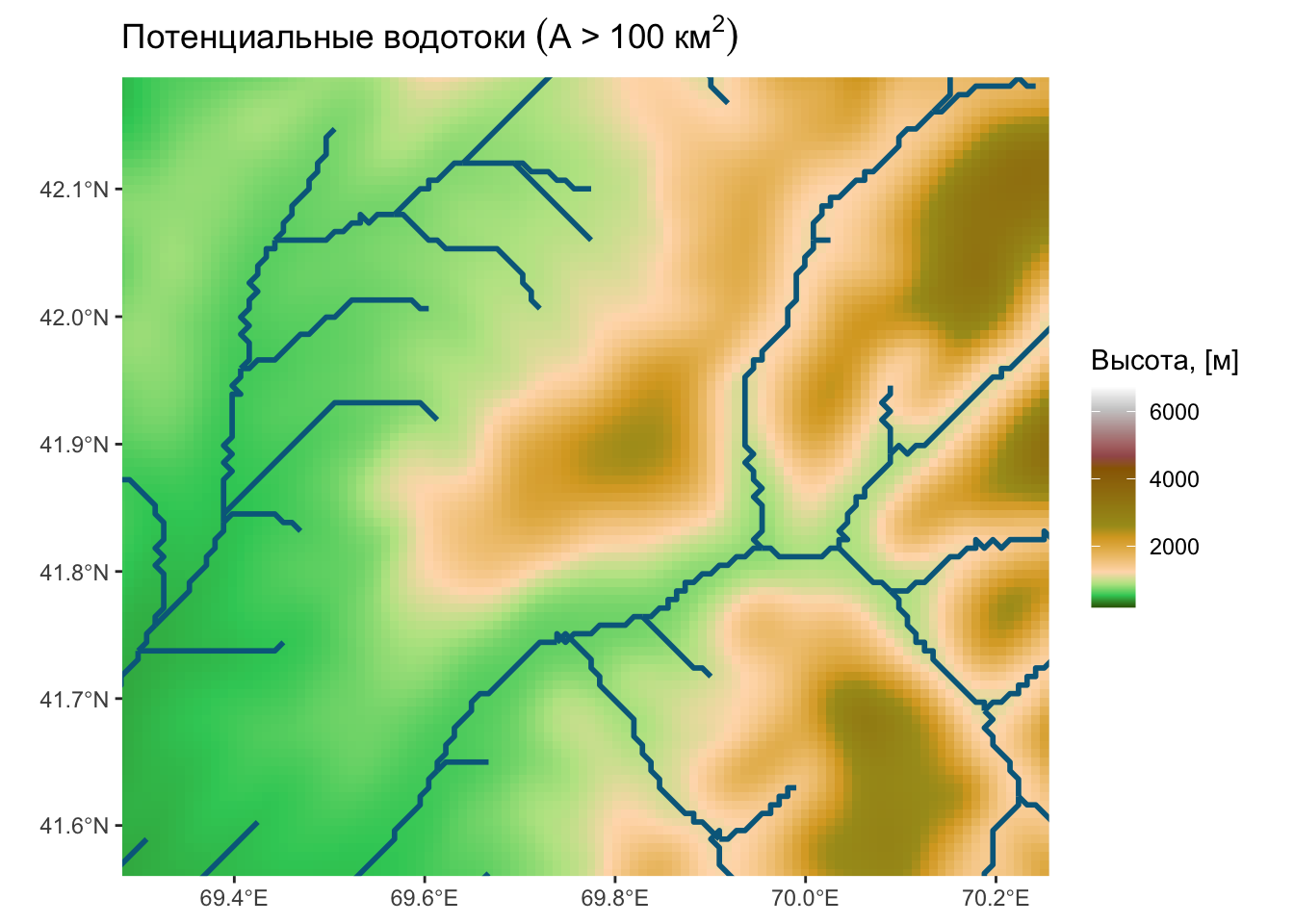
Потенциальные водотоки

Потенциальные водотоки — линии с высокой аккумуляцией стока.

1. Выделяют ячейки, аккумуляция стока в которых превышает заданную величину. На рисунке справа представлен пример для \(A \geq 2\).

Растровая маска потенциальных водотоков

Потенциальные водотоки

Потенциальные водотоки — линии с высокой аккумуляцией стока.

1. Выделяют ячейки, аккумуляция стока в которых превышает заданную величину. На рисунке справа представлен пример для \(A \geq 2\).
2. Выполняют трассировку линий по узлам выделенных ячеек с использованием растра направлений стока.

Потенциальные водотоки

Потенциальные водотоки

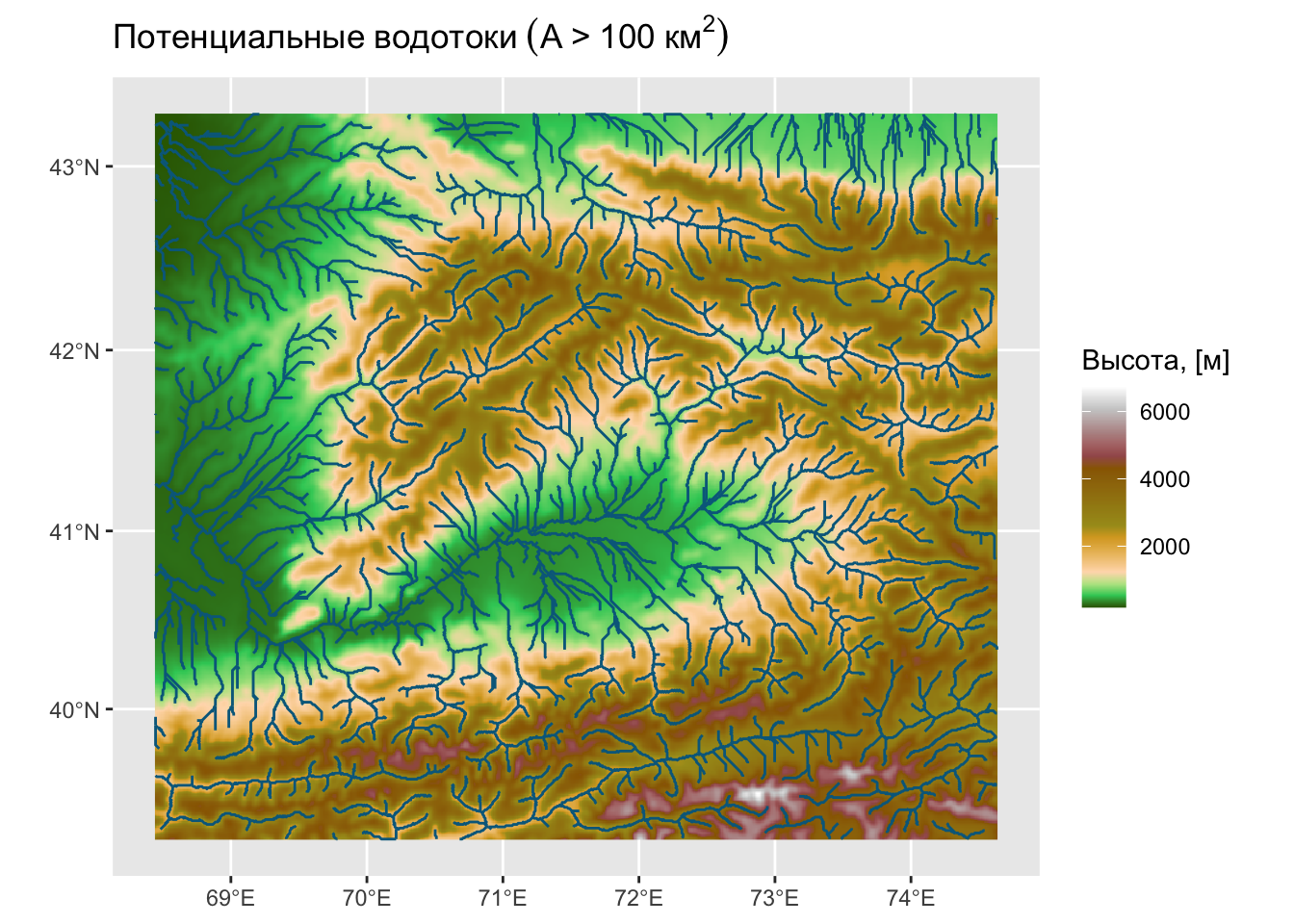
Потенциальные водотоки

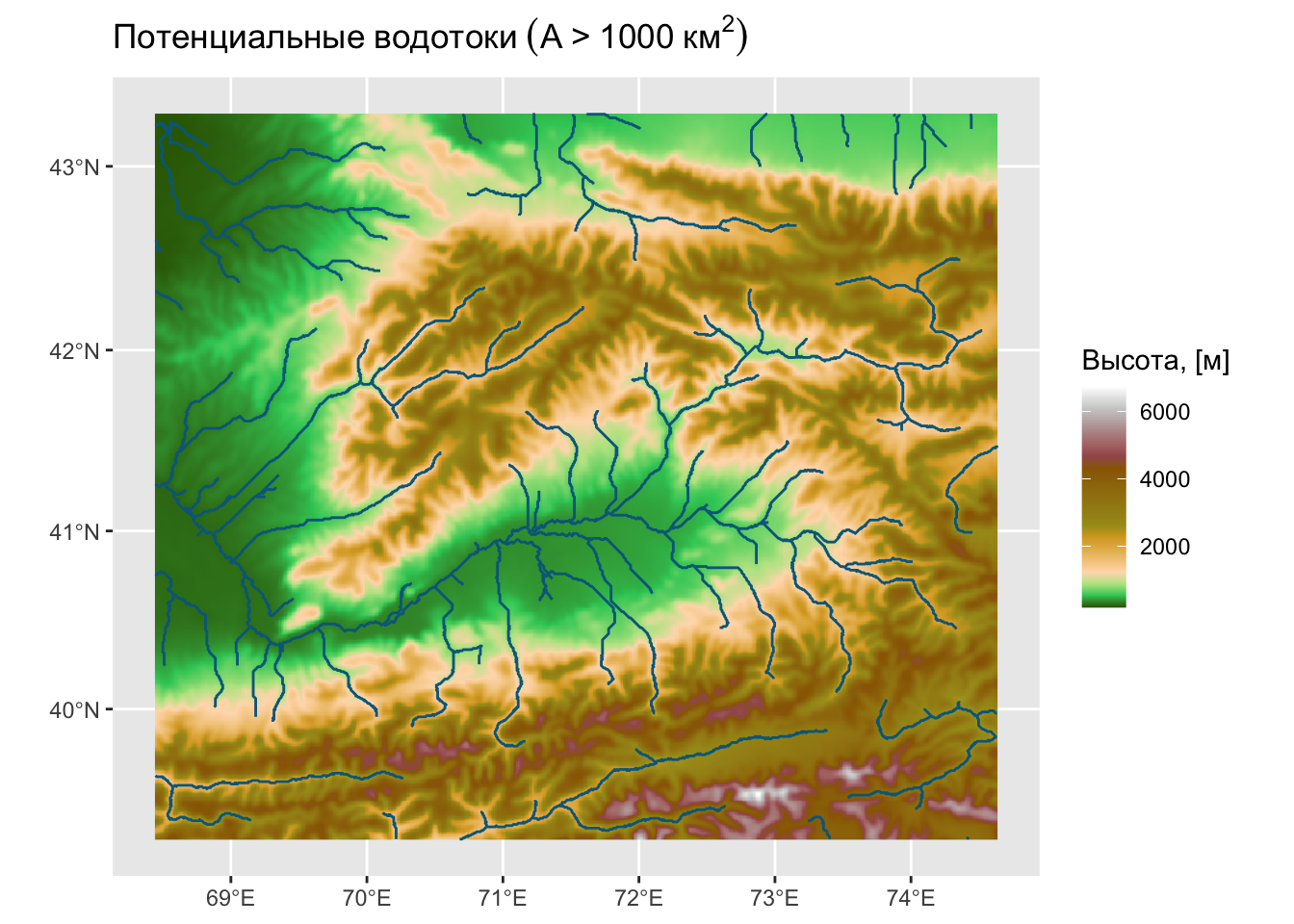
Потенциальные водотоки — крупно

Дренажный граф

Дренажный граф — частный случай сети потенциальных водотоков, который получается при \(A \geq 0\), а каждая линия соответствует одной связи в растре направлений стока.

Особенность

Дренажный граф представляет полную систему связей между ячейками ЦМР.

Дренажный граф

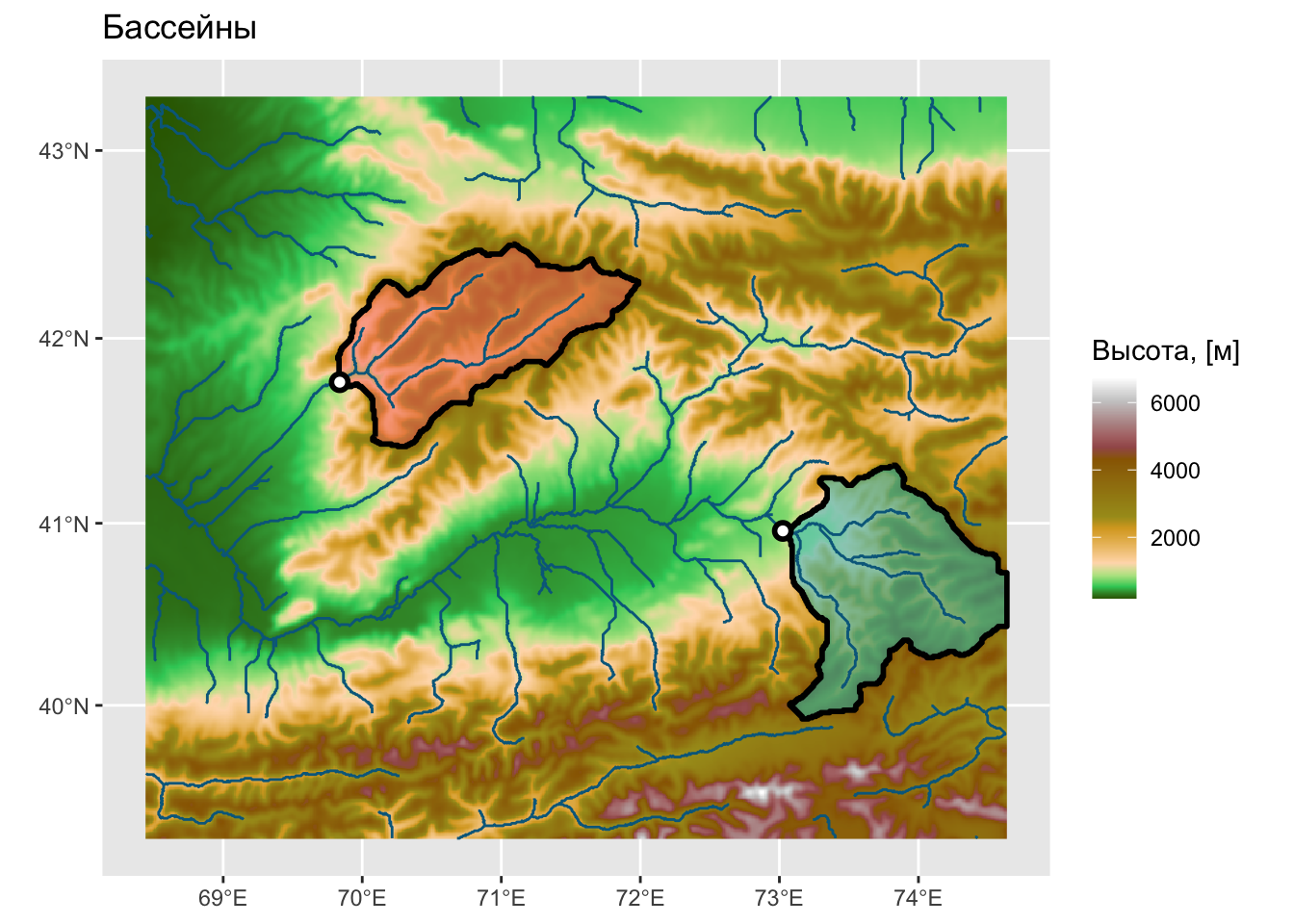
Бассейны

Бассейн получается путём поиска по модели направлений стока всех ячеек, сток из которых попадает в указанную ячейку.

Важно

Обычно на карте указывают точку для определения границы бассейна. Если она попала в ячейку с низкой аккумуляцией стока, то будет выделен бассейн малой площади.

Бассейн

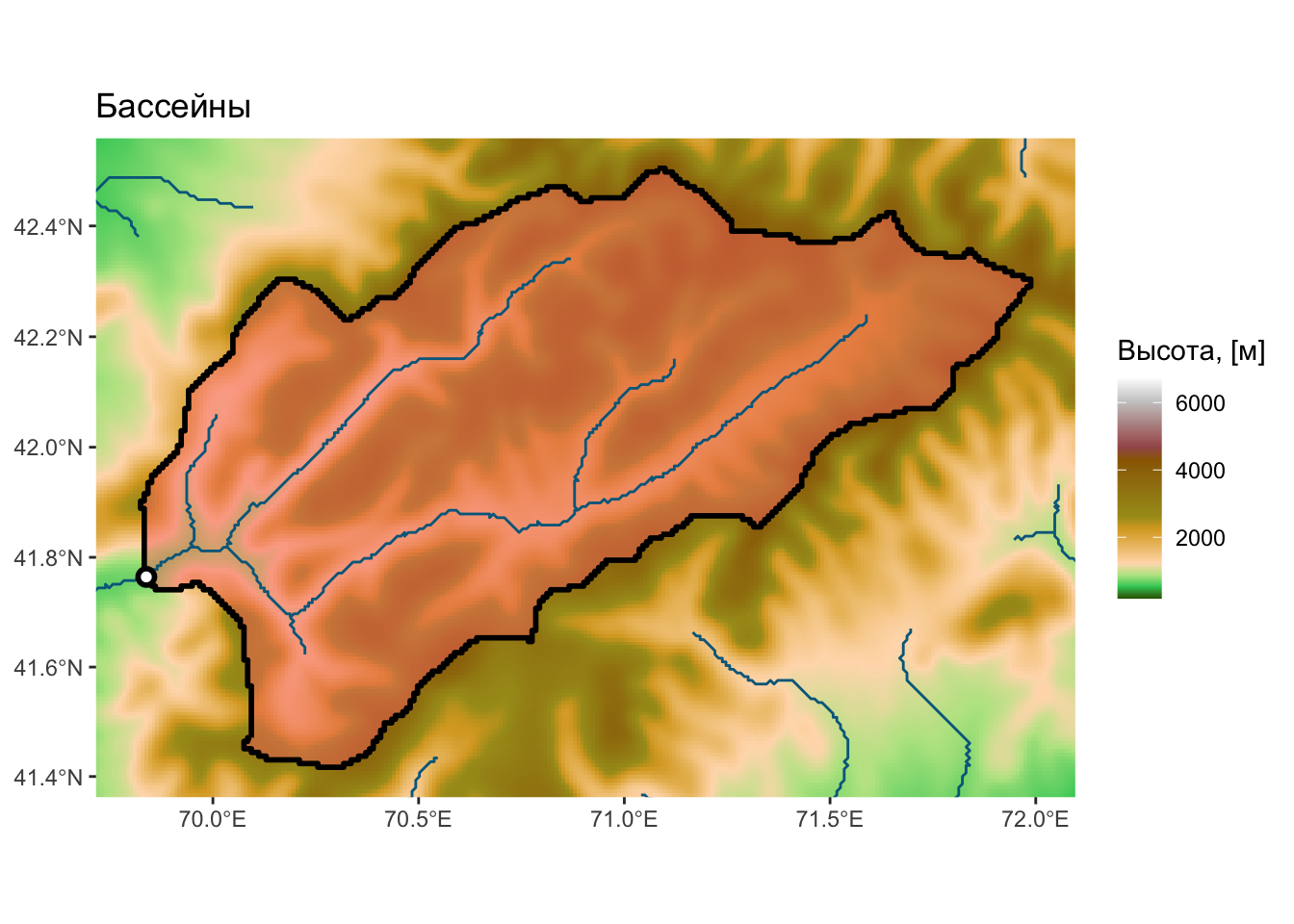
Бассейны

Бассейны — крупно

Гидрологический анализ ЦМР

Общая схема анализа выглядит следующим образом

flowchart TB
  A(ЦМР) --> B(Устранение ошибочных понижений)
  B --> C(Направления стока)
  C --> D(Аккумуляция стока)
  C --> E(Потенциальные водотоки)
  D --> E
  C --> F(Бассейны)
  D -.-> F

Словарик

Цифровая модель высот

Поверхность

Геоморфометрия

Производная

Уклон

Экспозиция

Кривизна

Отмывка

Направление стока

Аккумуляция стока

Бассейн / водосбор

Digital elevation model

Surface

Geomorphometry

Derivative

Slope

Aspect

Curvature

Hillshading

Flow direction

Flow accumulation

Basin / watershed

Библиография

Evans, I S. 1980. «An integrated system of terrain analysis and slope mapping». Zeitschrift fur Geomorphologie 36: 274–95.

O’Callaghan, John F, и David M Mark. 1984. «The extraction of drainage networks from digital elevation data». Computer Vision, Graphics, and Image Processing 28 (3): 323–44. https://doi.org/10.1016/S0734-189X(84)80011-0.

Open Geospatial Consortium Inc. 2005. «OGC 07-011 (ISO 19123:2005). The OpenGIS® Abstract Specification Topic 6: Schema for coverage geometry and functions». Open Geospatial Consortium Inc.