
Точечные процессы
Основы геоинформатики: лекция 11
11 апреля 2025 г.
Размещение
Размещение объектов в пространстве может как быть случайным, так и подчиняться определенным закономерностям.
Модели размещения позволяют описать характер размещения в виде количественных статистических параметров.
Как это работает?
Например, плотность размещения деревьев можно связать с крутизной и экспозицией склона.
Точечный процесс и паттерн
Точечный процесс — случайный процесс \(\mathbf P\) , реализациями которого являются точечные паттерны.
Точечный паттерн — неупоря-доченное множество точек:
\[\mathbf{p} = \{p_1, p_2,...p_n\}\]
Количество точек \(n = n(\mathbf p)\) может быть любым неотрицательным числом.
Эталонные распределения
Характер пространственного распределения устанавливается путем сравнения с эталонными моделями распределений.
Распространены следующие эталонные распределения:
- Абсолютно случайное
однородное
неоднородное
- Кластерное
- Регулярное
Экспериментальный подход
- В пределах той же территории генерируется множество случайных паттернов, состоящих из того же числа точек.
- Статистические характеристики случайных паттернов сравниваются с аналогичными характеристиками фактического распределения.
- Делается вывод о том, к какому распределению принадлежит фактическое.
Абс. случайное распределение
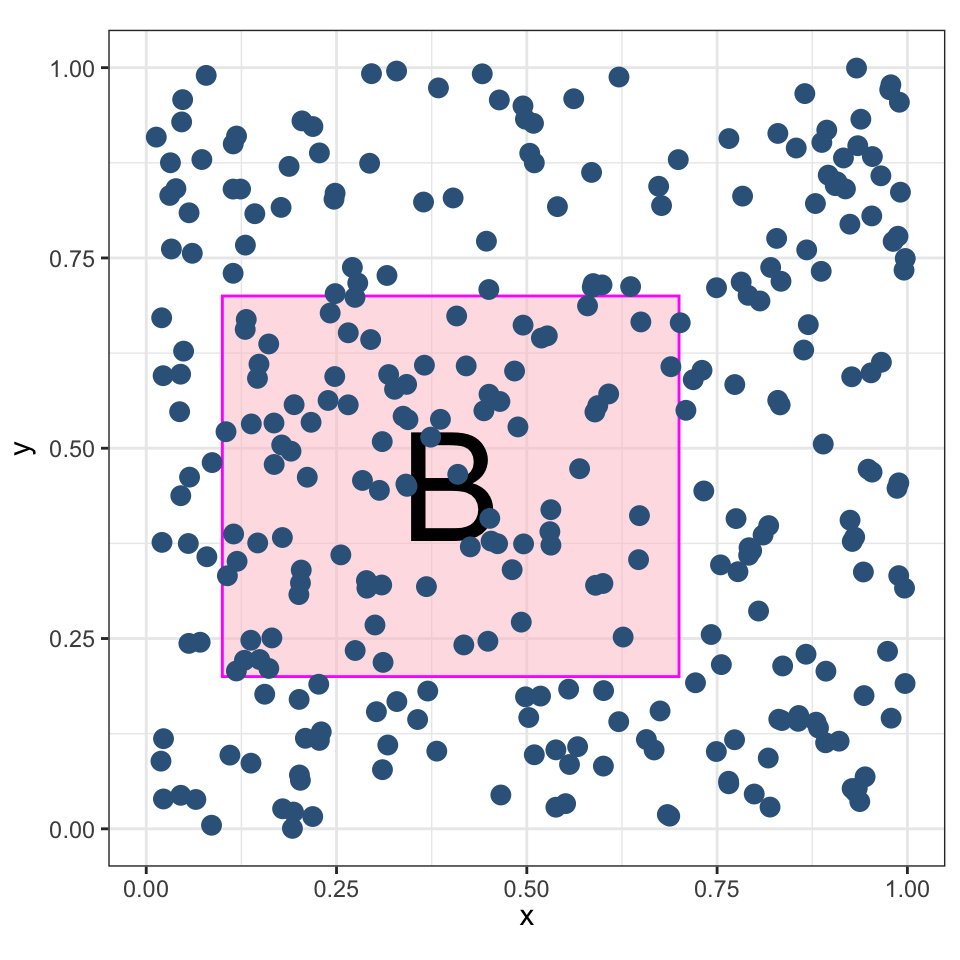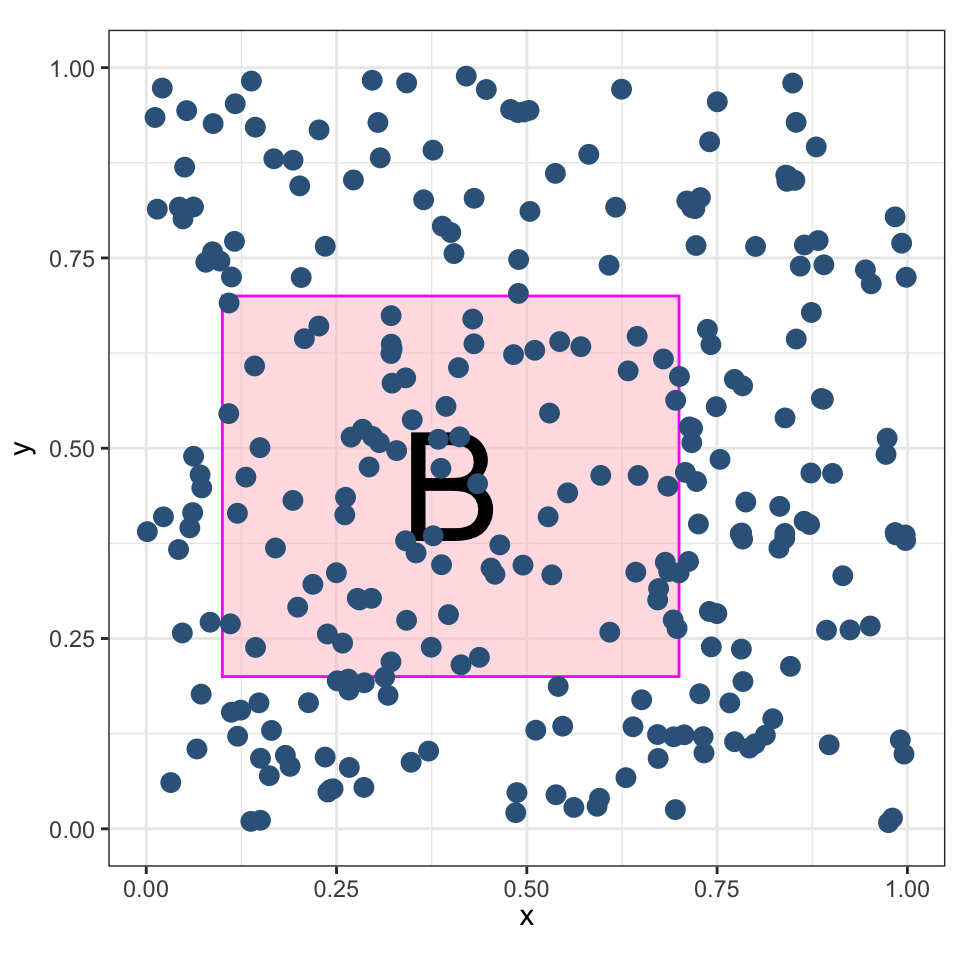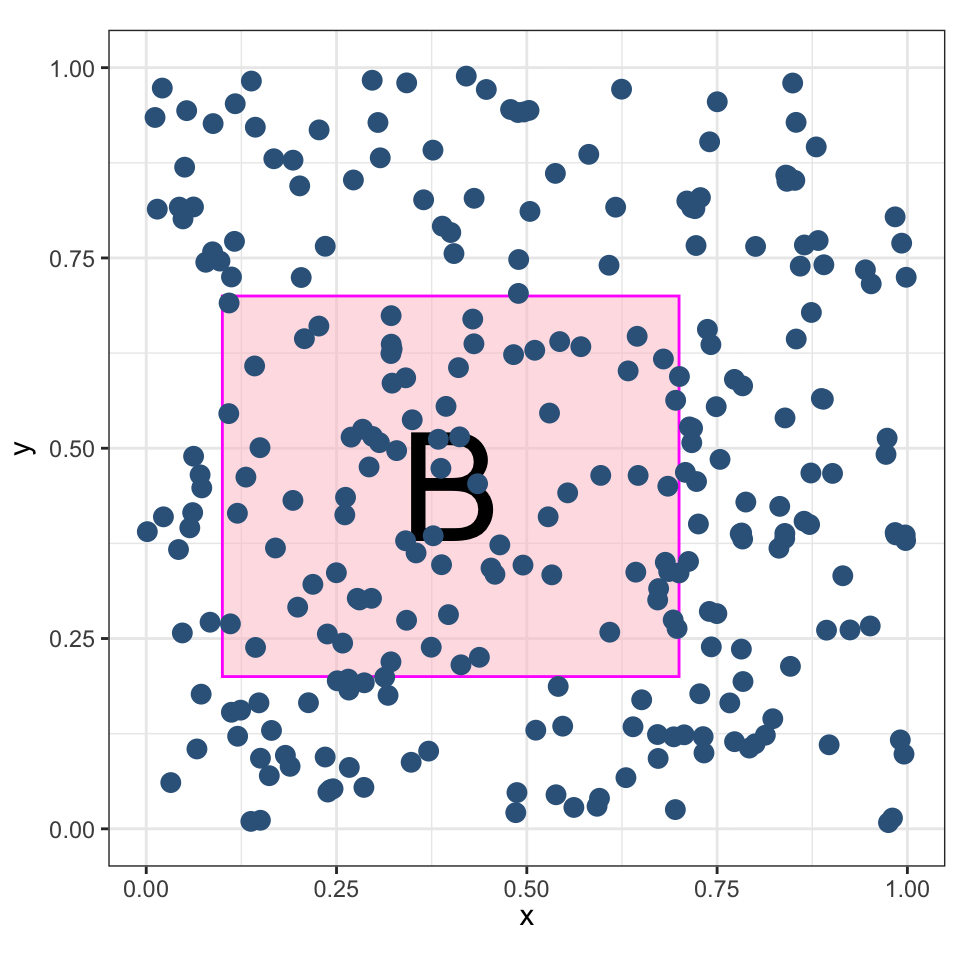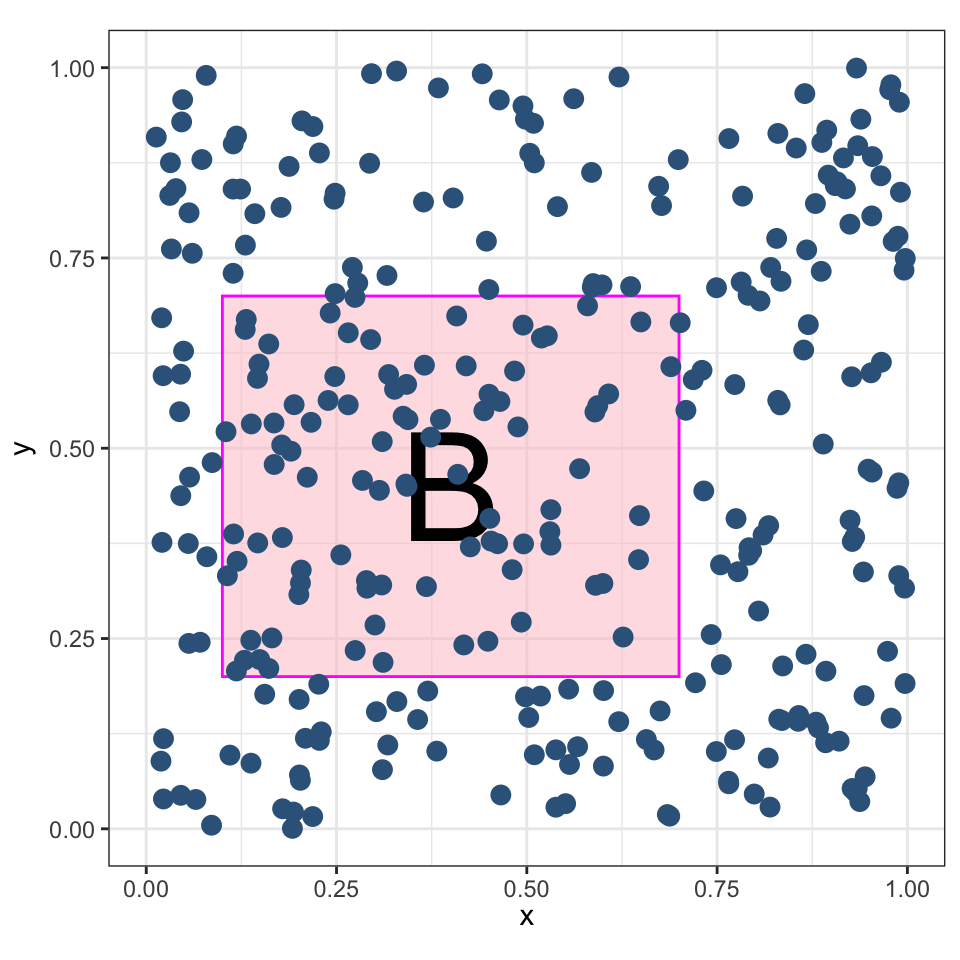
Координаты \(X\) и \(Y\) имеют равномерное распределение в заданной области \(B\).
Ожидаемое количество точек, попадающих в регион \(B\) пропорционально его площади:
\[ \mu = \mathbb E\big[n(\mathbf{P} \cap B)\big] = \lambda |B|, \]
где \(\lambda\) — интенсивность.
Интенсивность
Интенсивность точечного процесса — ожидаемое количество точек на единицу площади.
Абс. случайное распределение
Вероятность того, что в области \(B\) окажется ровно \(k\) точек имеет распределение Пуассона \(\Pi(\mu)\):
\[ \mathbb{P}\{N = k\} = e^{-\mu} \frac{\mu^k}{k!} \]
Пуассоновский процесс
Абсолютно случайный точечный процесс также называют пуассоновским.
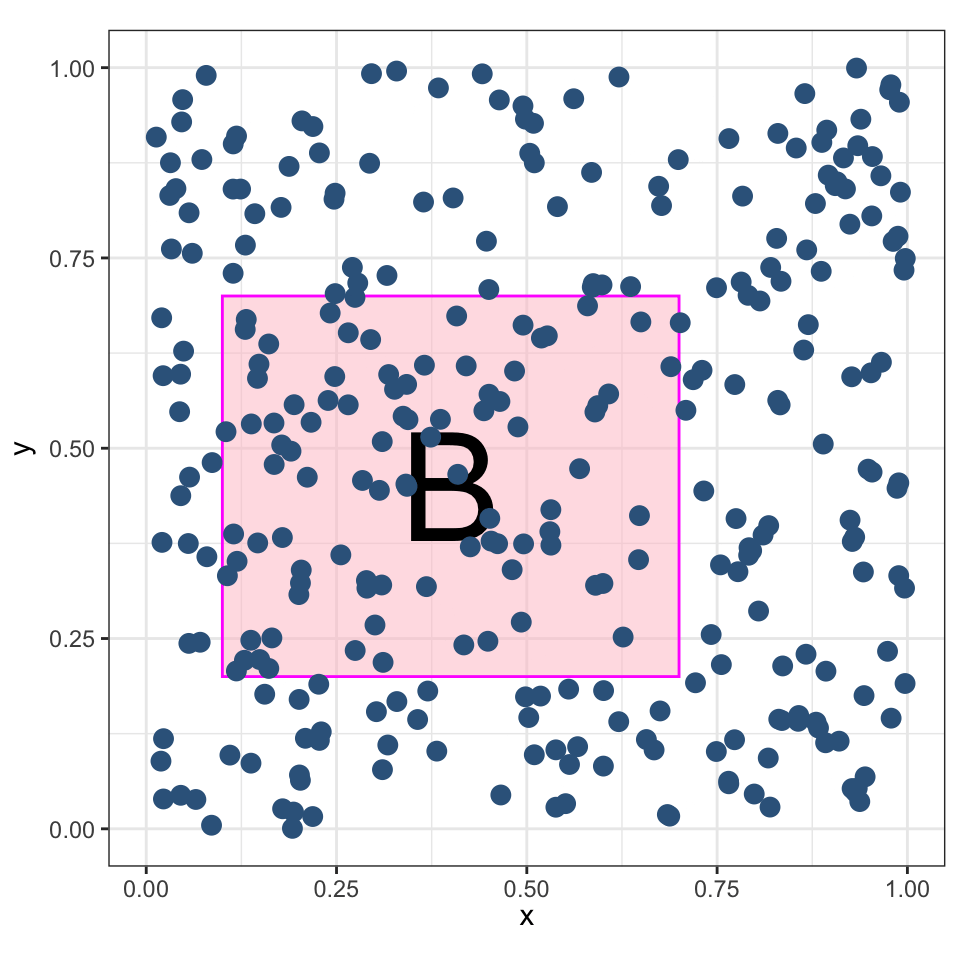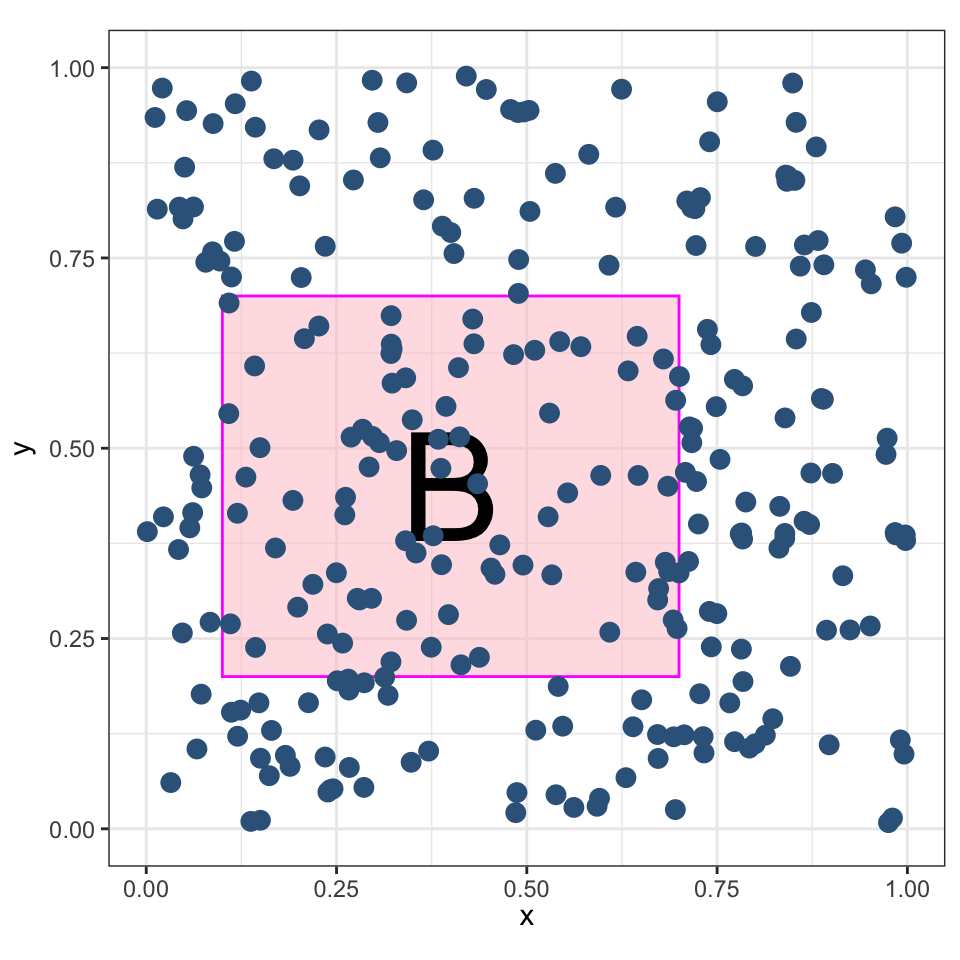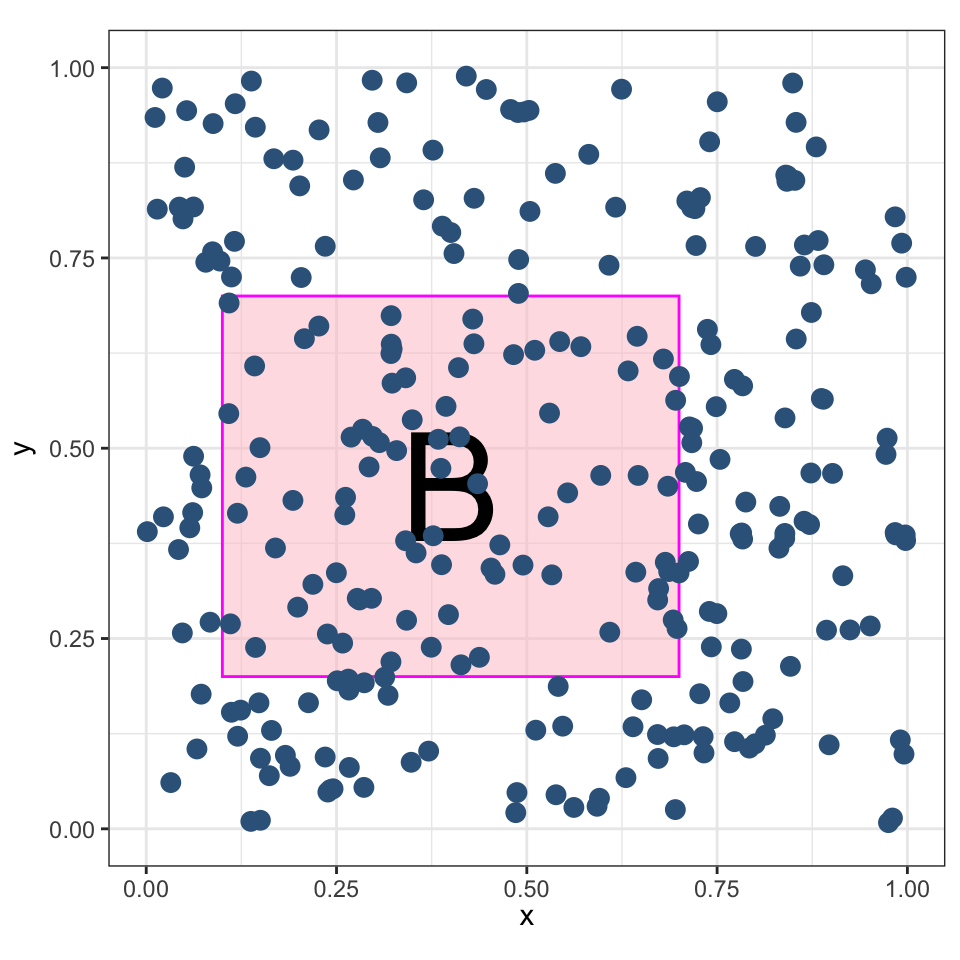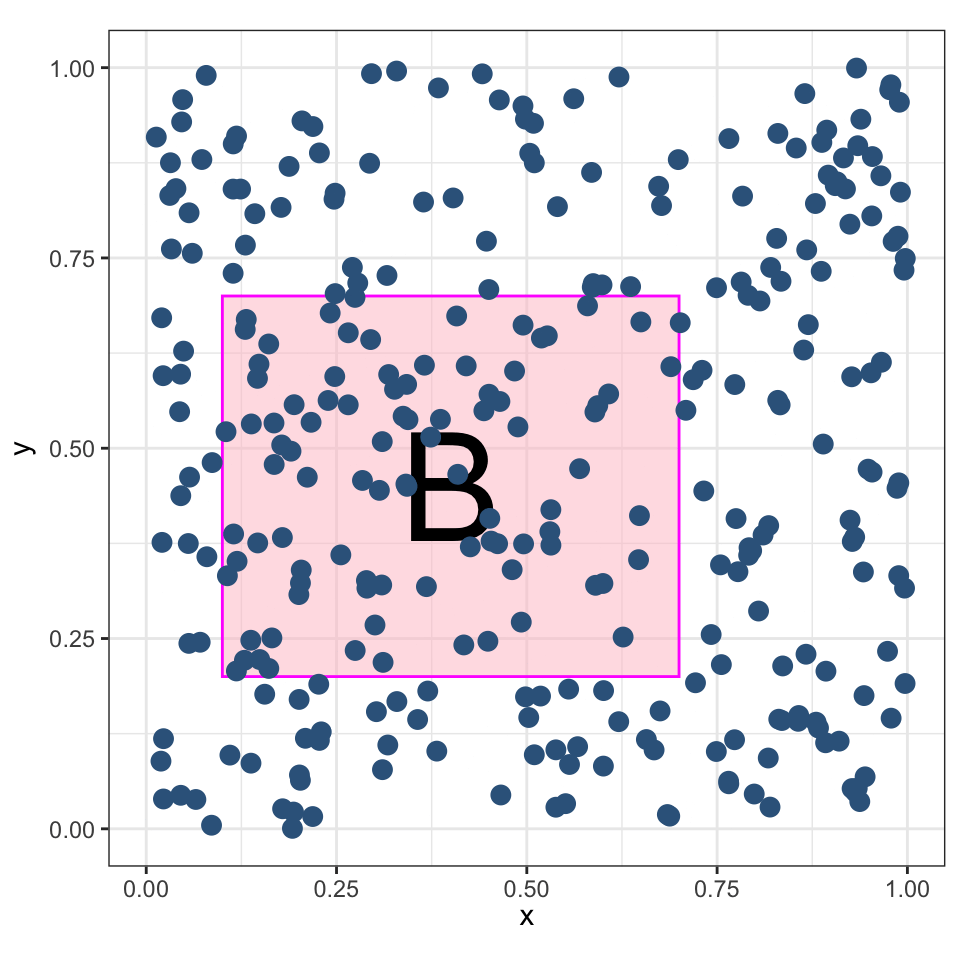
Однородный пуассоновский процесс
Пуассоновский процесс называется однородным, если его интенсивность не зависит от местоположения. То есть, \(\lambda\) — константа.
Однородный пуассоновский процесс
Распределение населенных пунктов в Турции
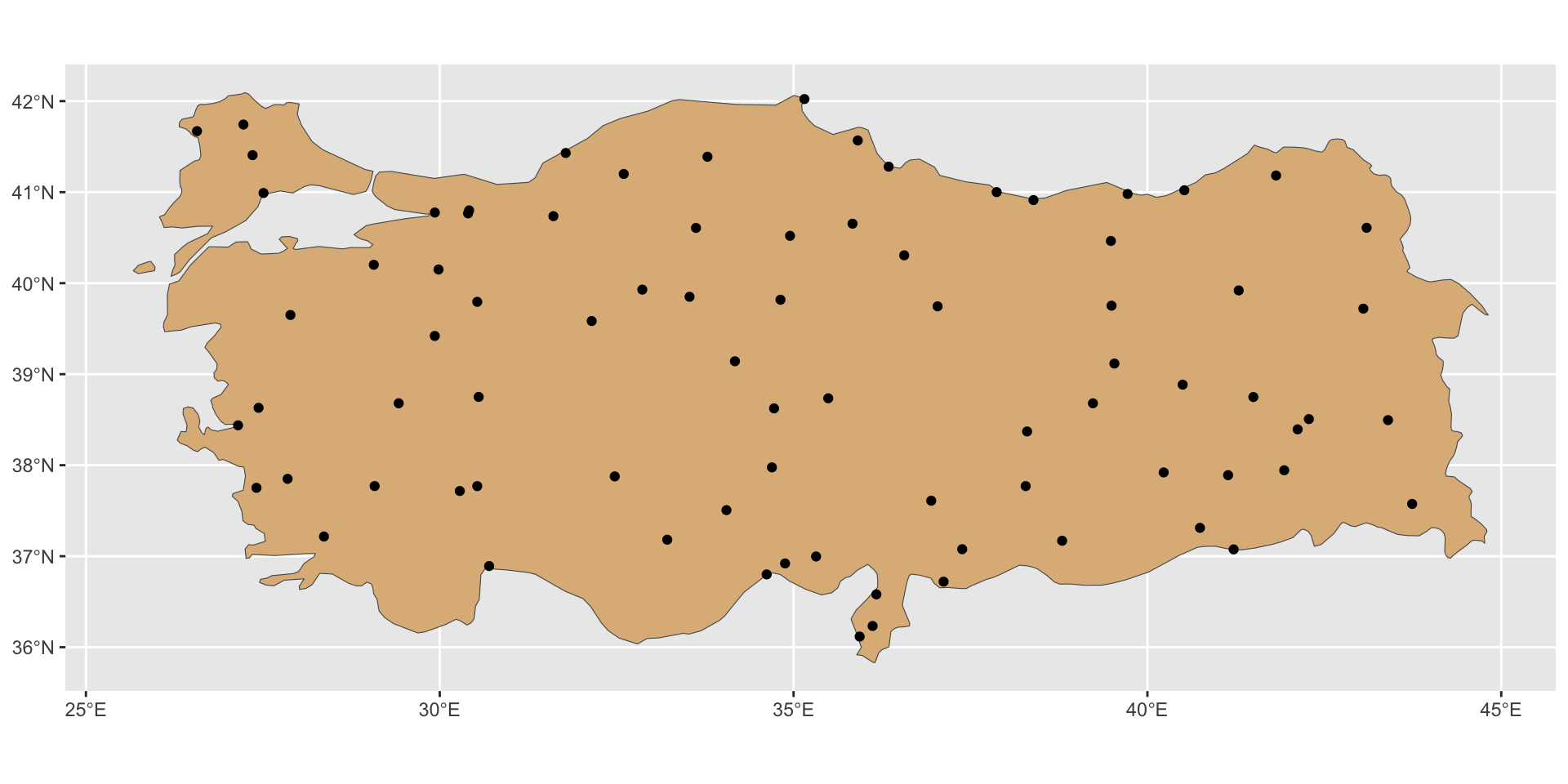
Симуляция Пуассоновского процесса
Пусть дана область \(B = [x_{min}, x_{max}] \times [y_{min}, y_{max}]\) и интенсивность точечного процесса \(\lambda\).
Необходимо сгенерировать:
Случайное число \(N\), имеющее распределение Пуассона с параметром \(\mu = \lambda |B|\).
\(N\) координат \(x_i = x_1, x_2, ..., x_N\), имеющих равномерное распределение на промежутке \([x_{min}, x_{max}]\).
\(N\) координат \(y_i = y_1, y_2, ..., y_N\), имеющих равномерное распределение на промежутке \([y_{min}, y_{max}]\).
Точечный паттерн \(p_i = (x_i, y_i)\) собирается из полученных координат.
Неоднородная случайность
- Неоднородный пуассоновский процесс имеет функцию интенсивности \(\lambda(x,y)\), которая зависит от местоположения.
- Ожидаемое количество точек в регионе \(B\):
\[ \mu = \mathbb E\big[n(\mathbf{P} \cap B)\big] = \int_B \lambda(x,y) dx dy \]
Процесс Кокса
Процесс Кокса — неоднородный Пуассоновский процесс, в котором \(\lambda\) — случайная величина.
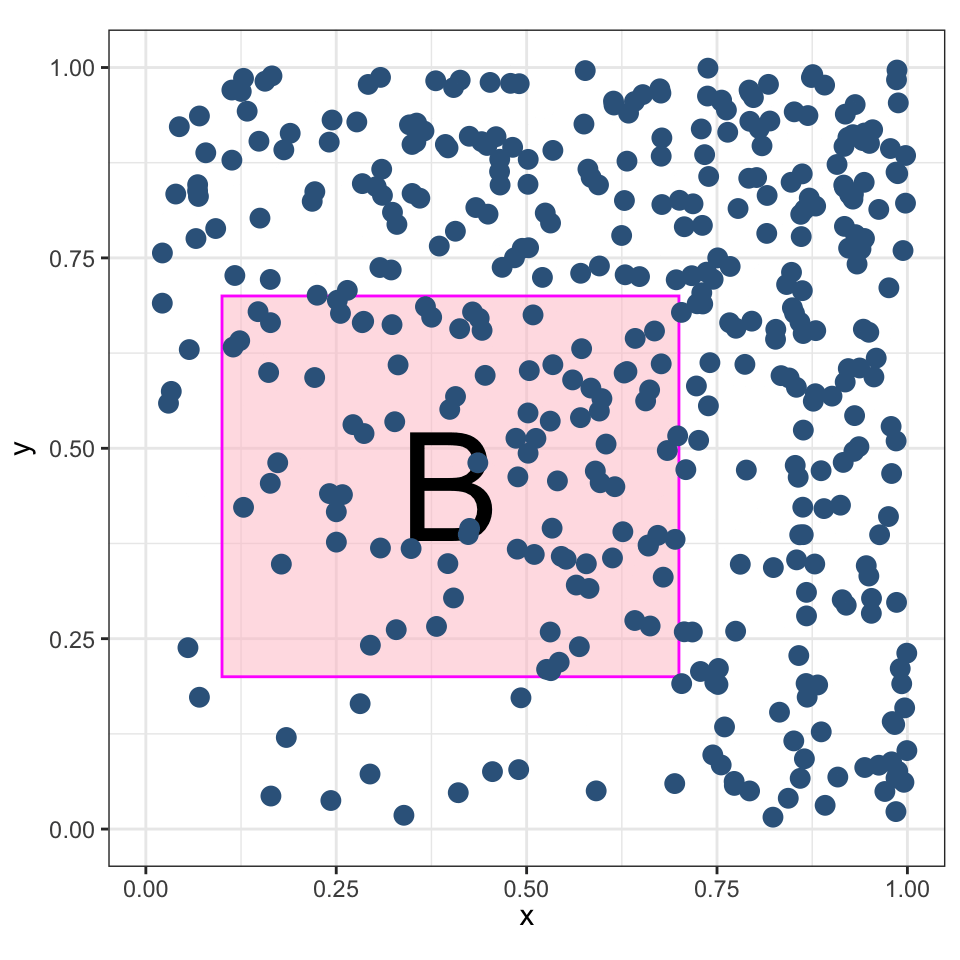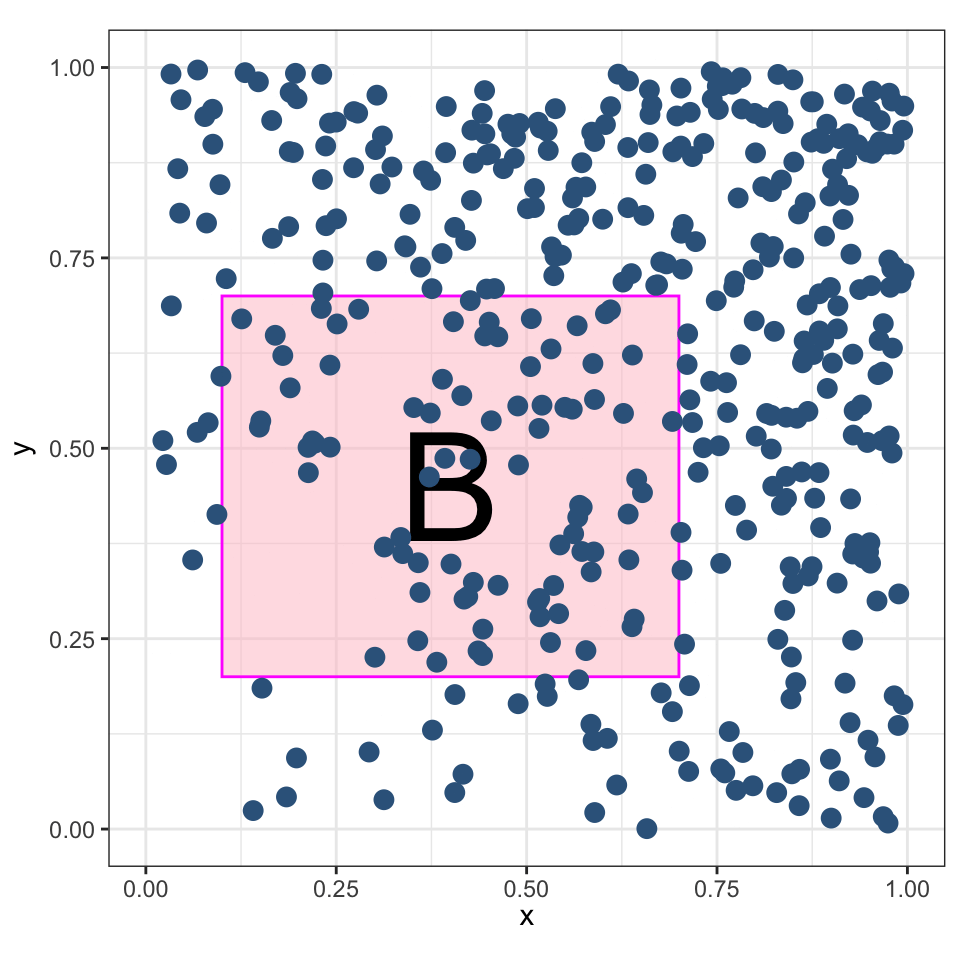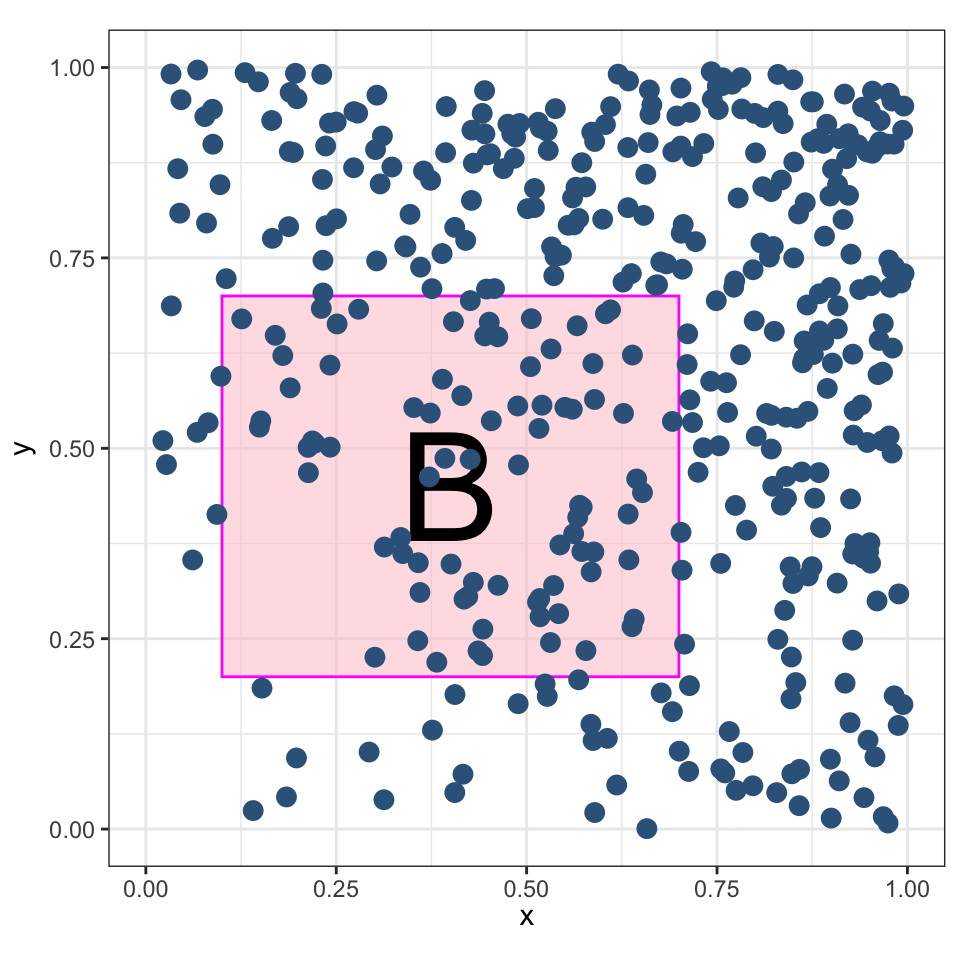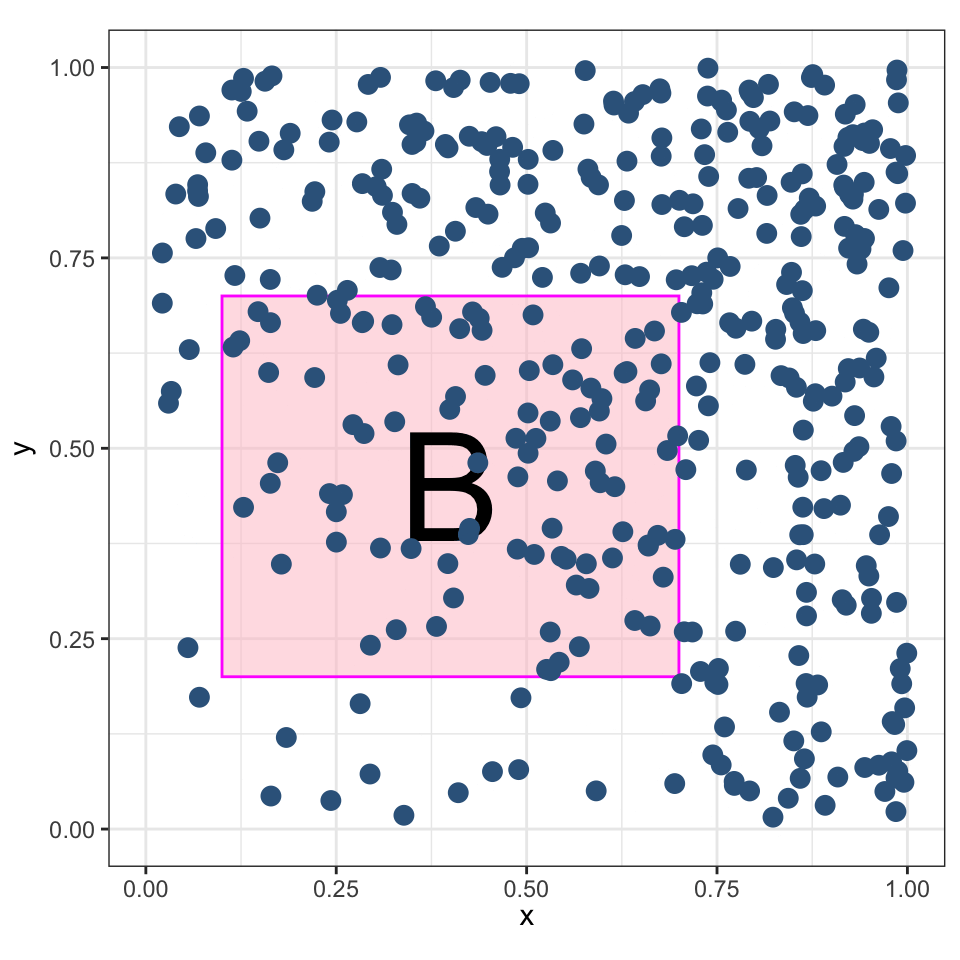
\[ \lambda(x,y) = x + y^2 \]
Неоднородная случайность
Распределение населенных пунктов в Китае
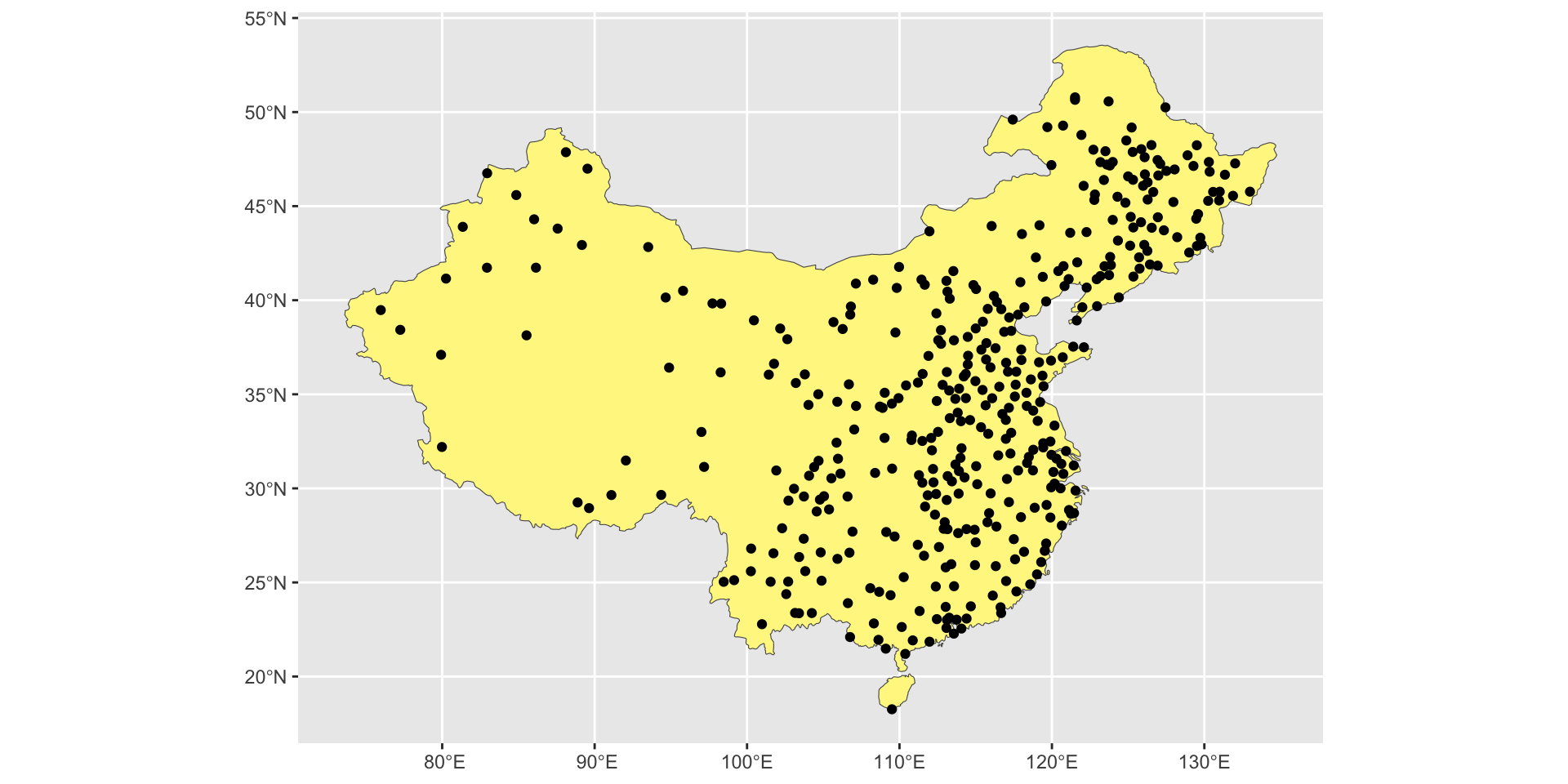
Симуляция неоднородного процесса
Метод Льюиса-Шедлера (Lewis-Shedler thinning):
Генерируется однородный Пуассоновской процесс с интенсивностью \(\lambda_{max} = \max\big[\lambda(x, y)\big]\).
Осуществляется случайное прореживание (исключение) точек с вероятностью сохранения точки \(\mathbb P(x,y) = \lambda(x,y) / \lambda_{max}\), пропорциональной функции интенсивности.
Чтобы понять, будет ли точка исключена, генерируется случайное число 0 или 1, имеющее распределение Бернулли с вероятностью положительного исхода \(\mathbb P = \mathbb P(x,y)\).
Граничный эффект
Центробежная конфигурация (тяготеет к границе) может свидетельствовать о:
влиянии объектов (границы) на конфигурацию точек
наличии определенного ресурса у границы
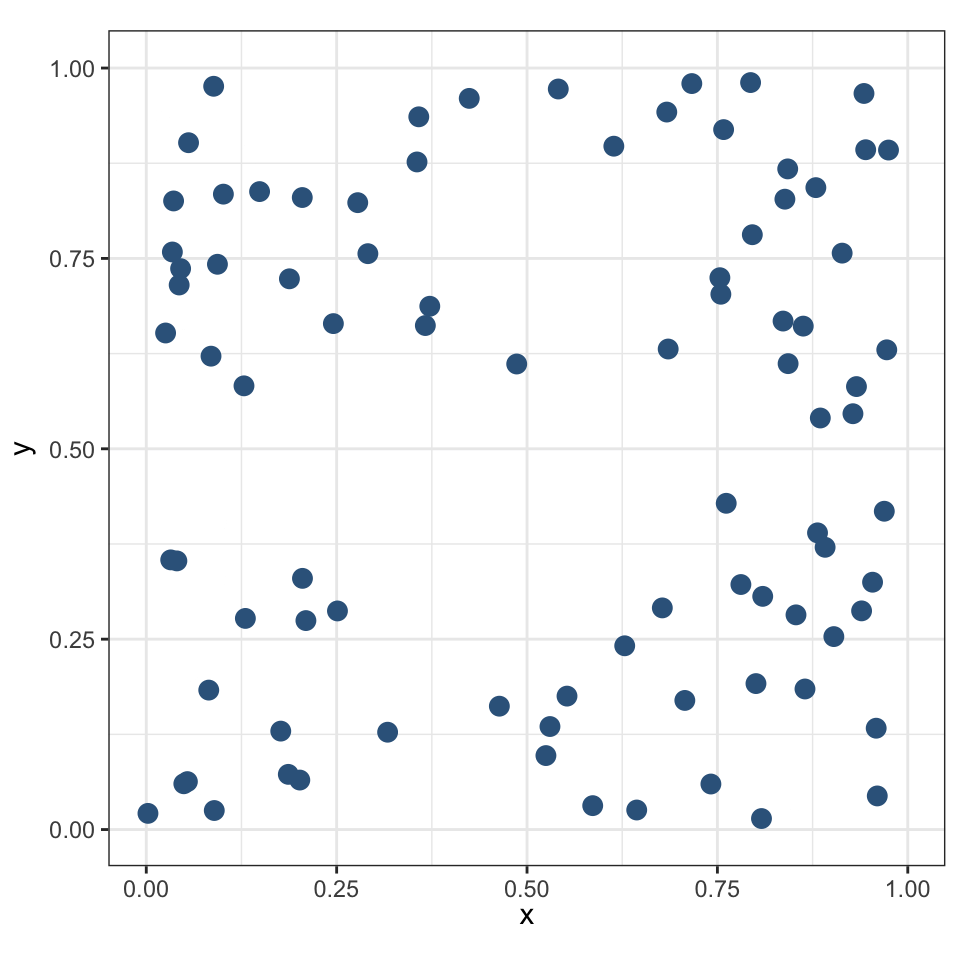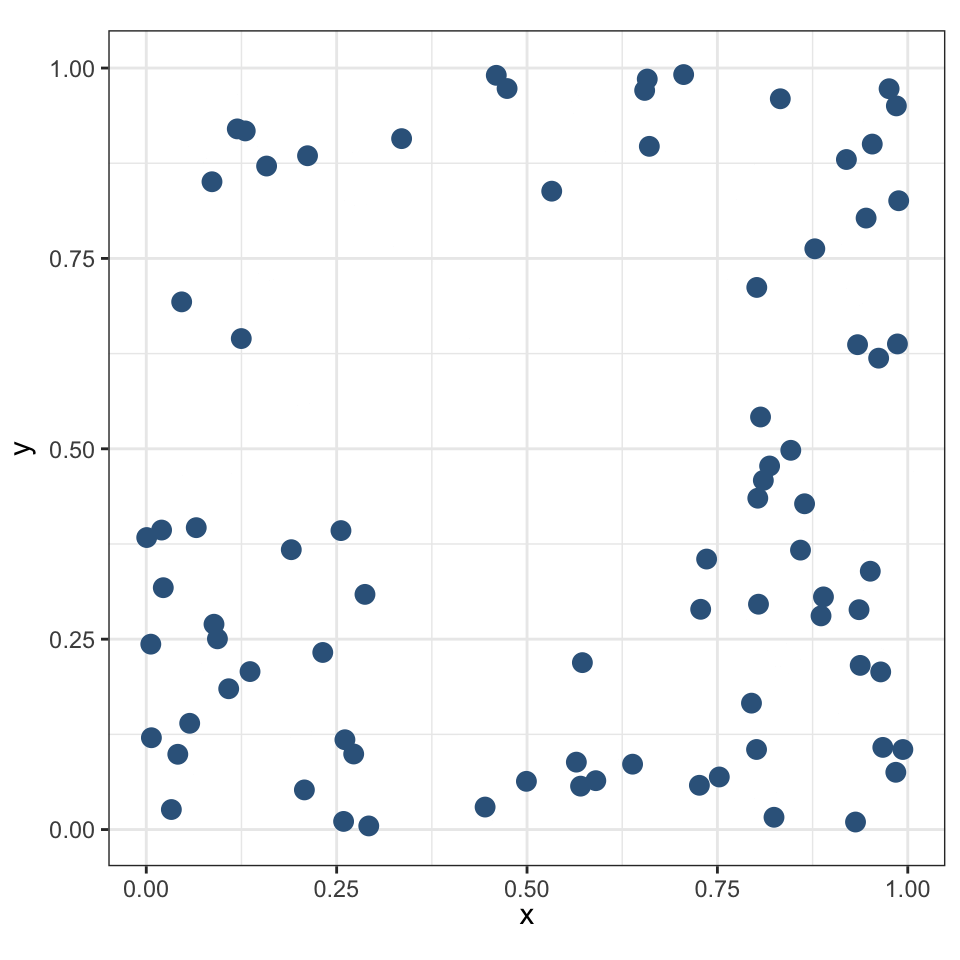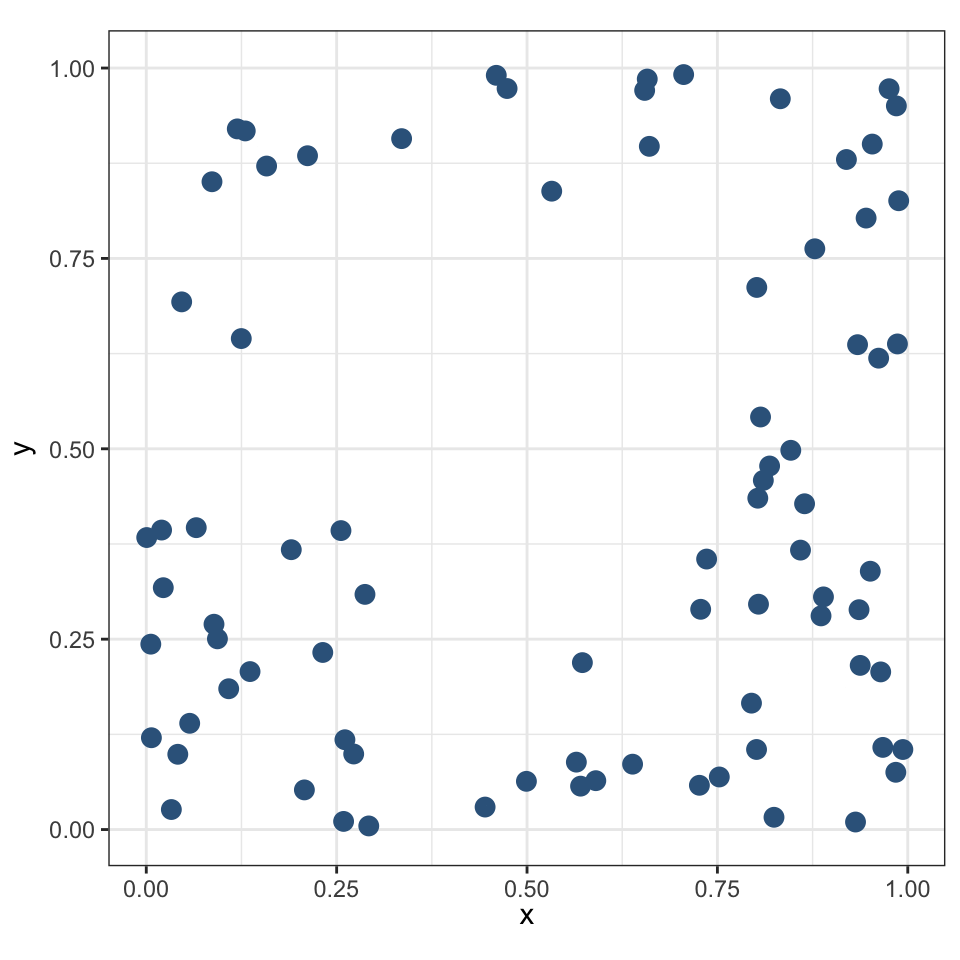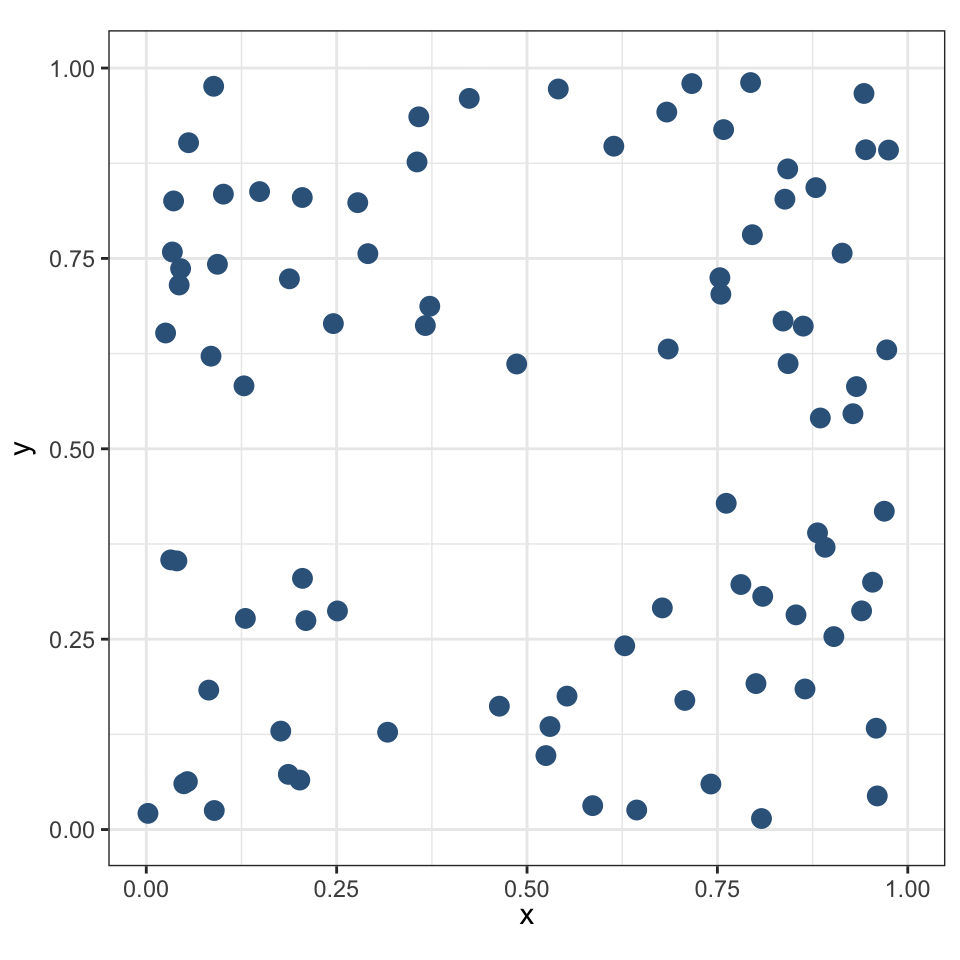
Граничный эффект
Распределение населенных пунктов в Австралии
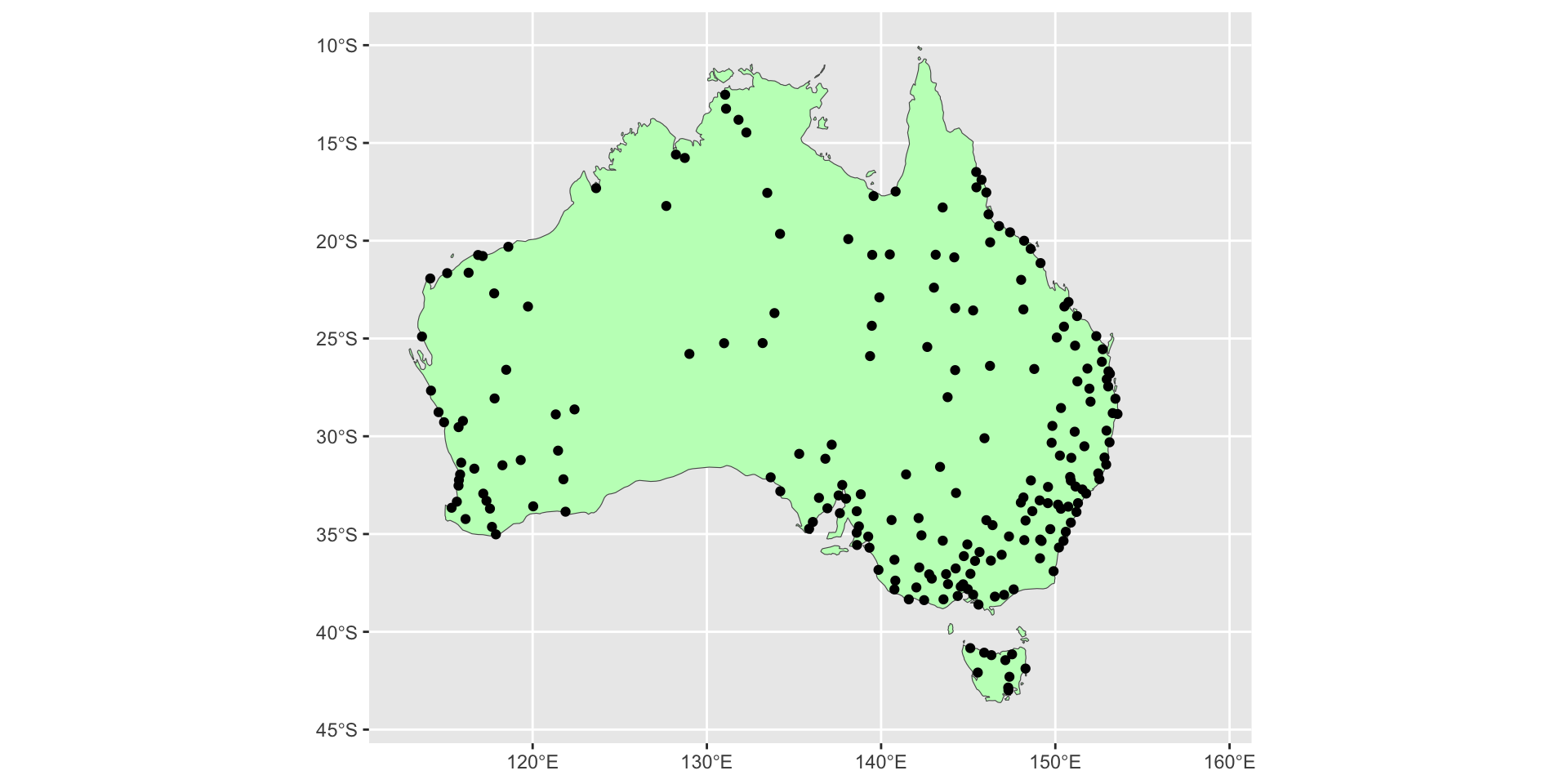
Граничный эффект
Центростремительная конфигурация (отталкивается от границы) может свидетельствовать о:
неблагоприятности приграничных территорий для данного типа точек
сосредоточении ресурсов в центральной части региона
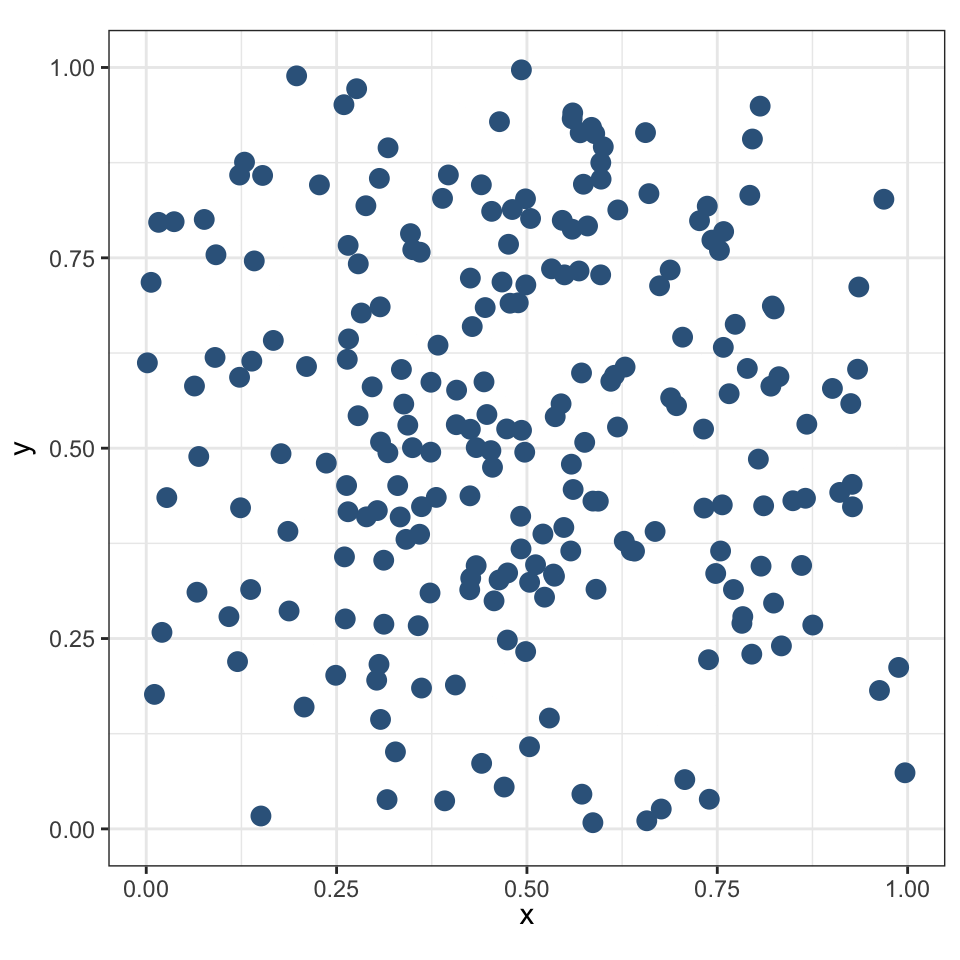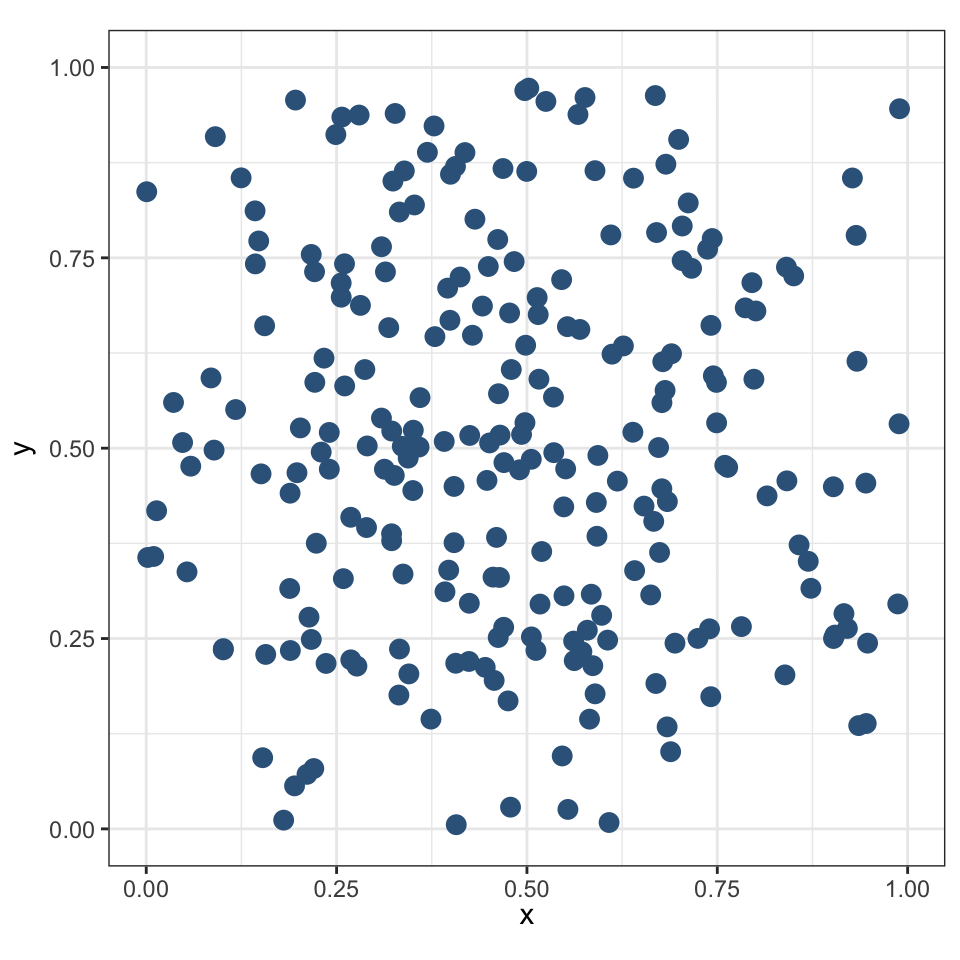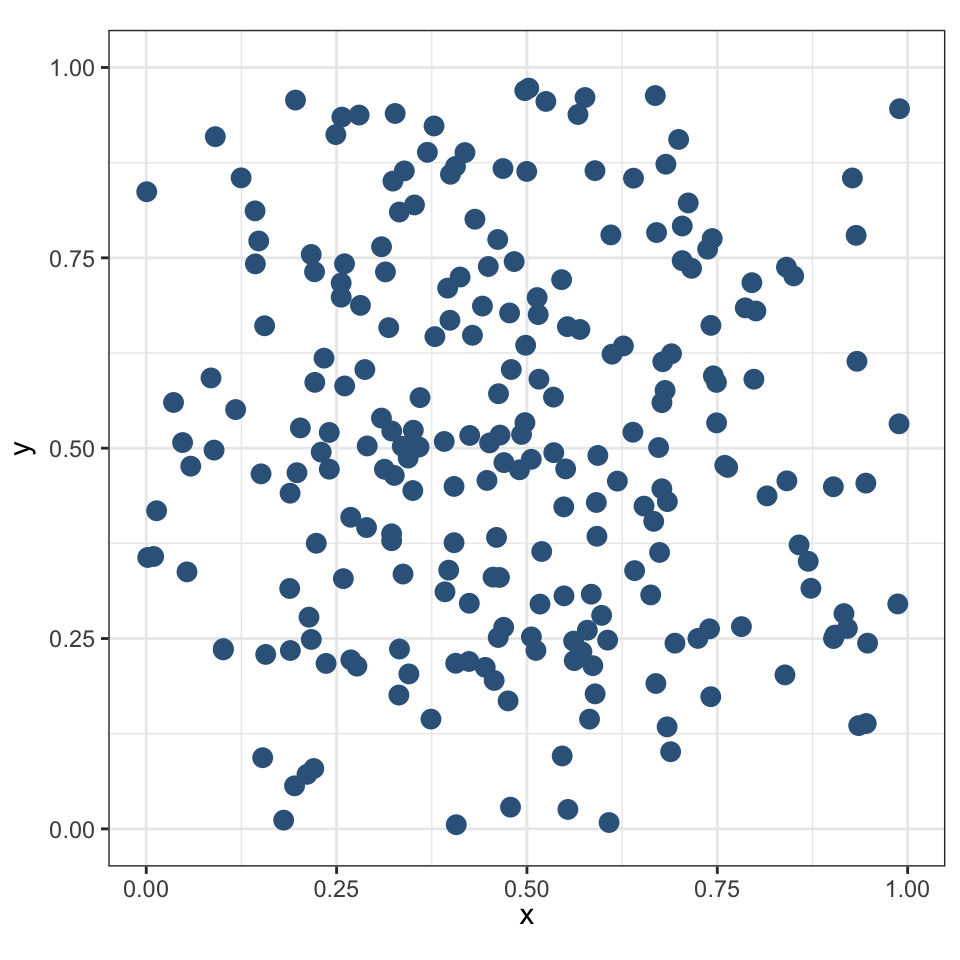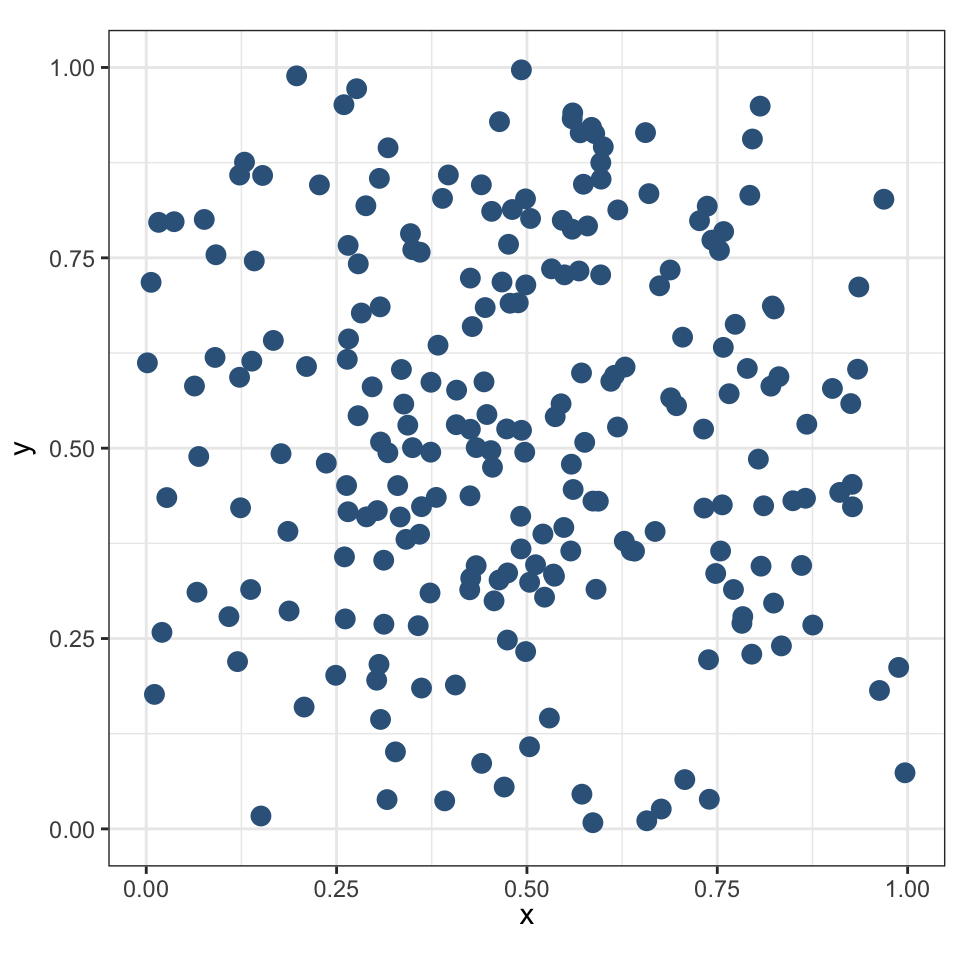
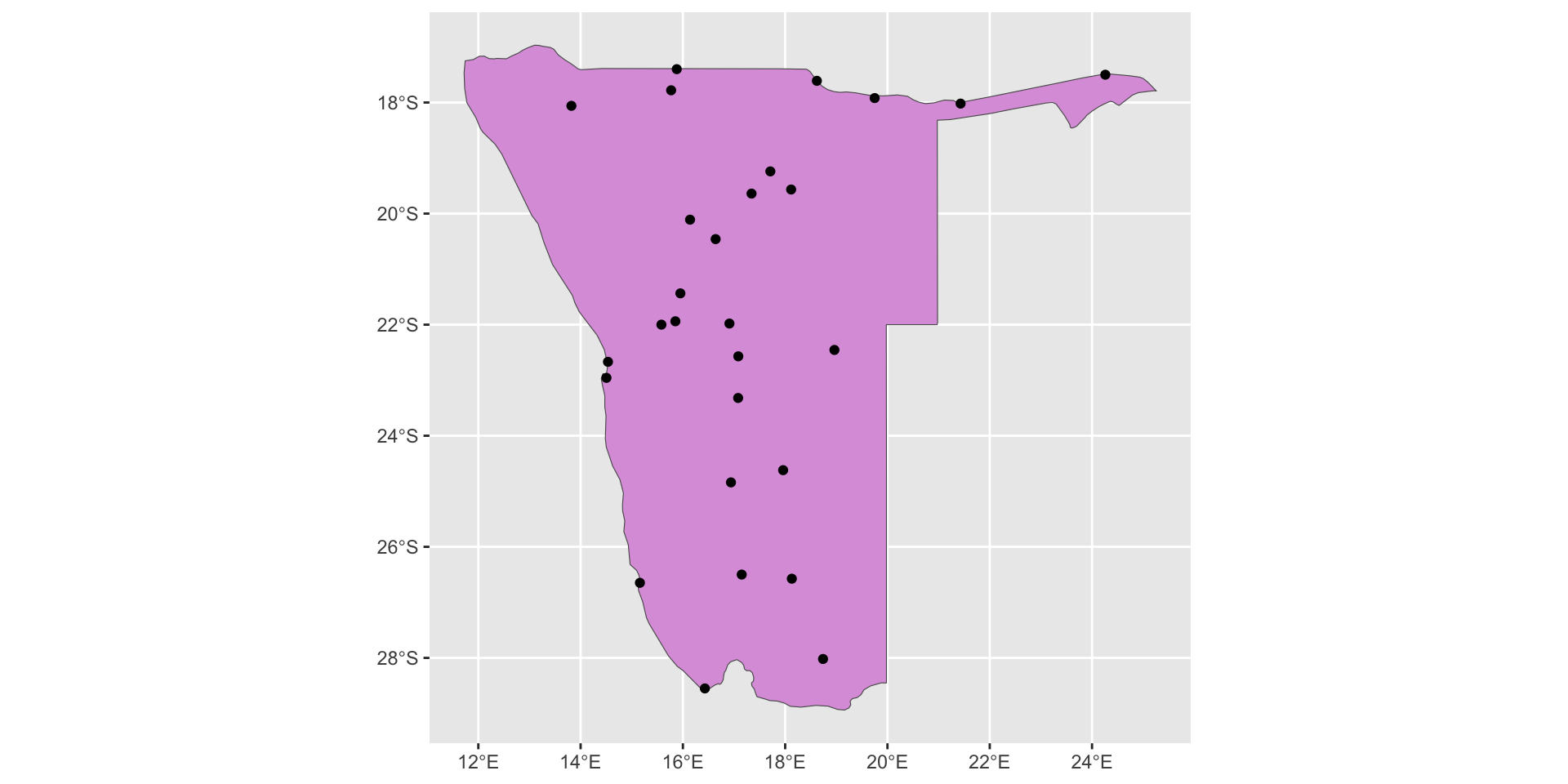
Граничный эффект
Распределение населенных пунктов в Намибии
Кластерное распределение
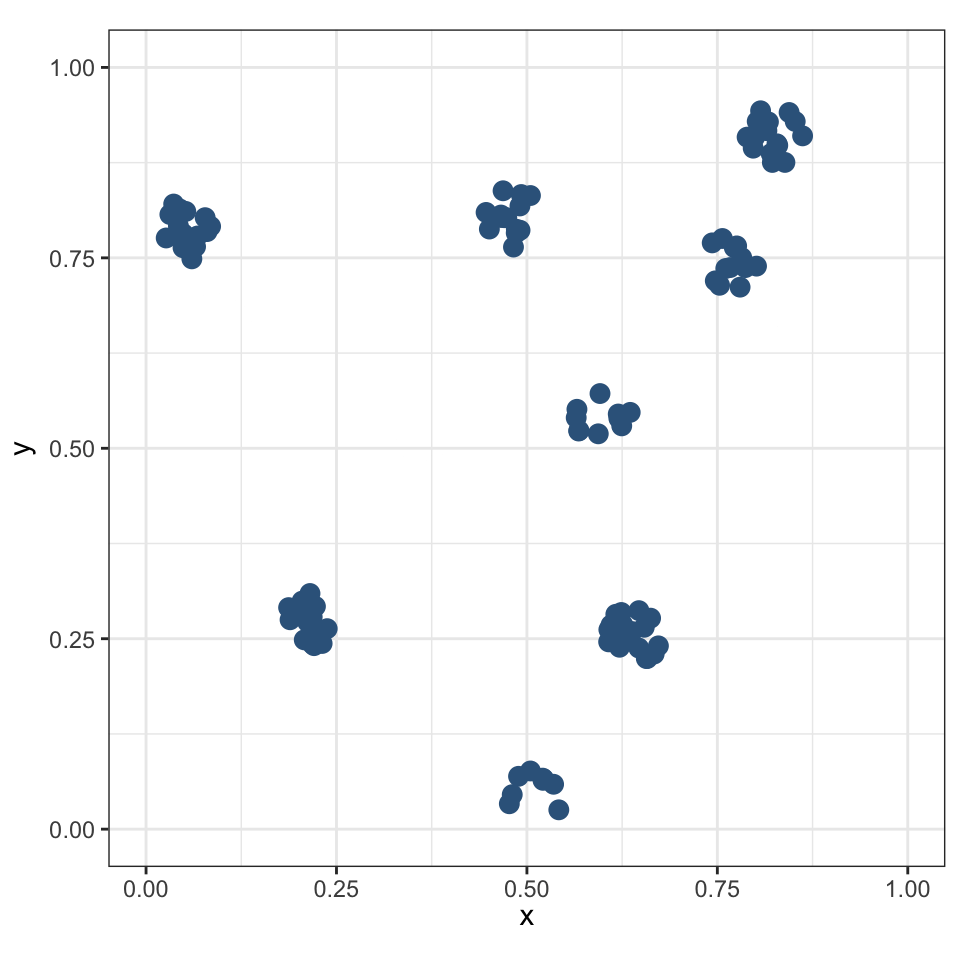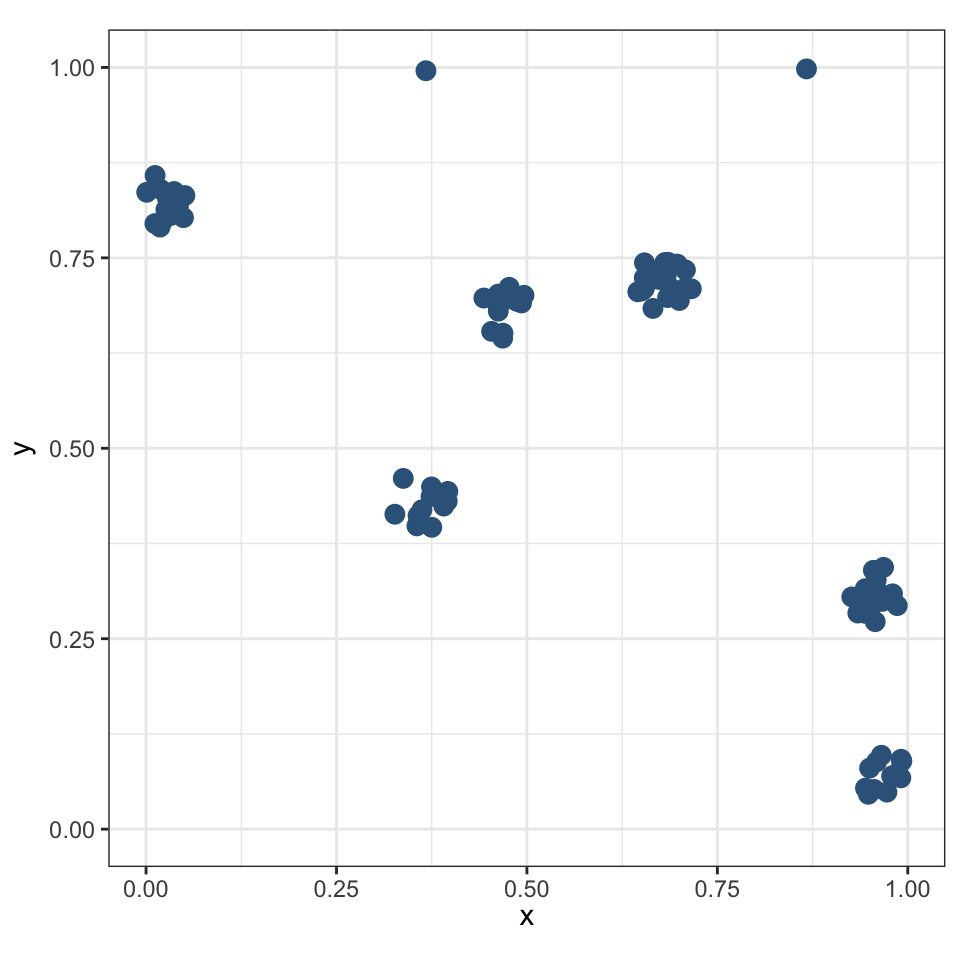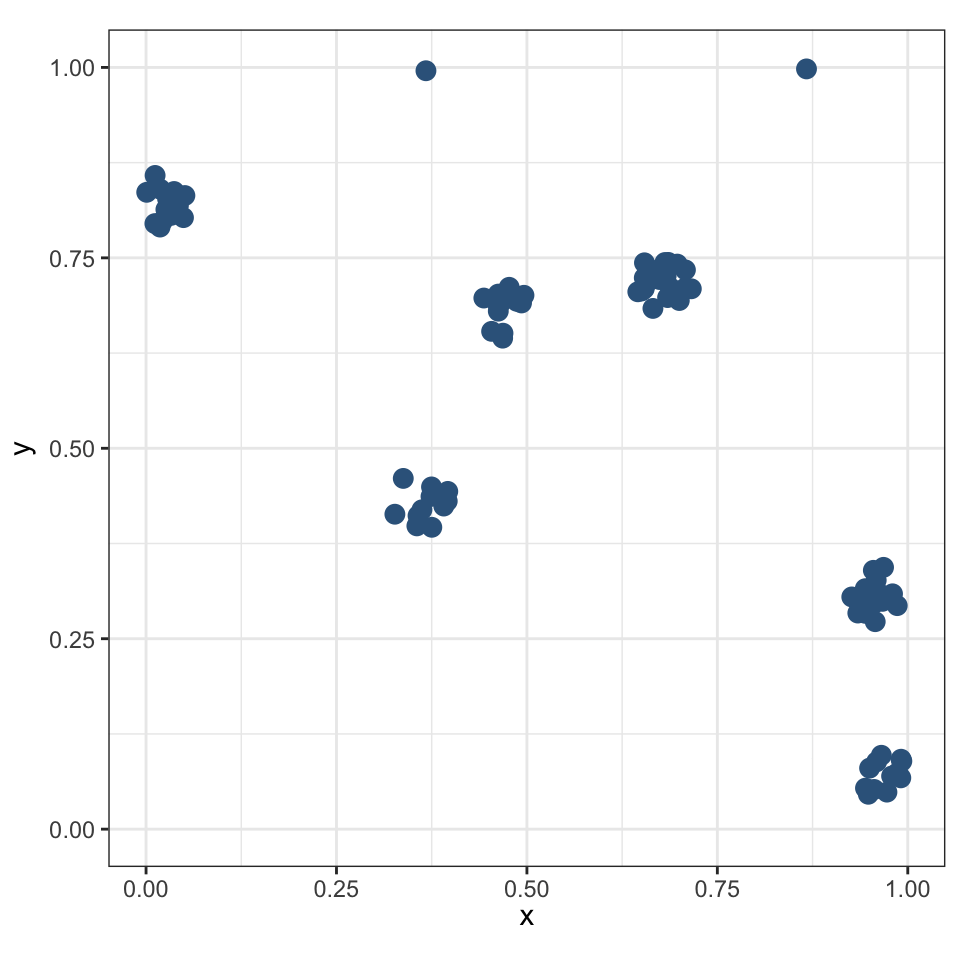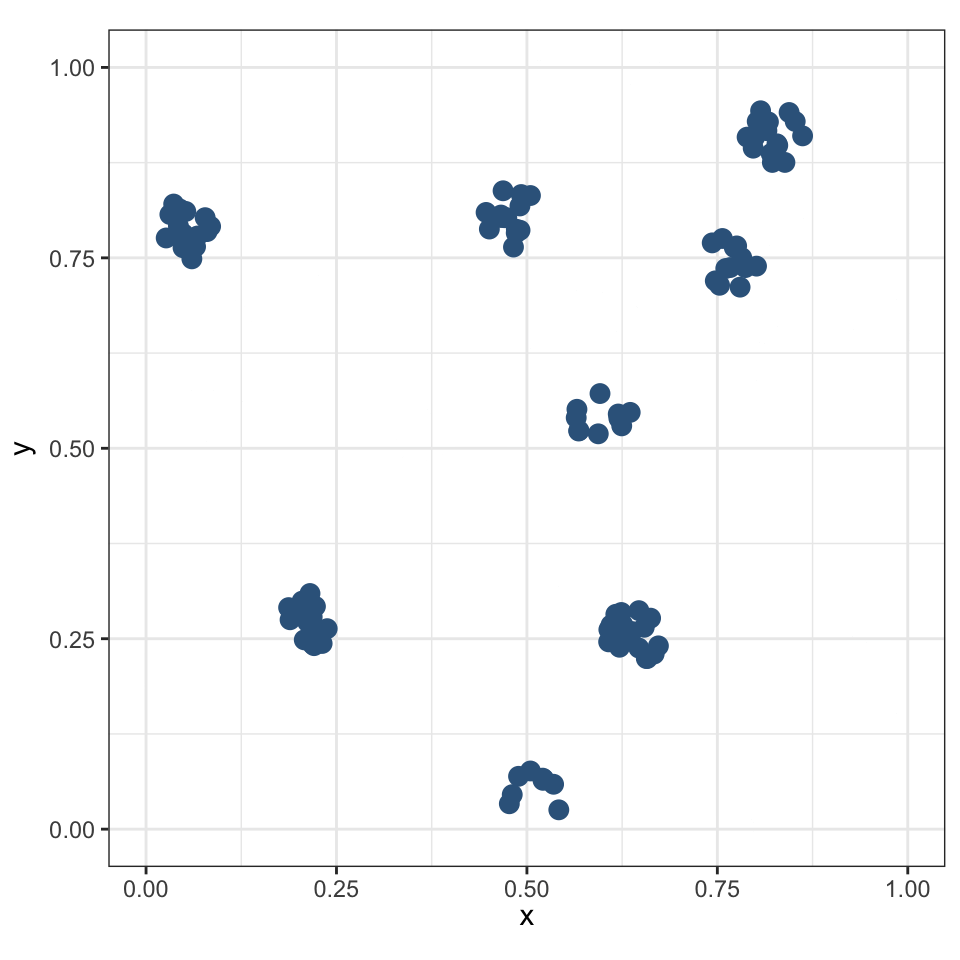
Кластерным называется распределение, в котором точки имеют тенденцию образовывать скопления — кластеры.
Точки из одного кластера в среднем значительно ближе, чем точки из разных кластеров.
Кластер
Объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определёнными свойствами.
Кластерное распределение
Распределение населенных пунктов в Египте
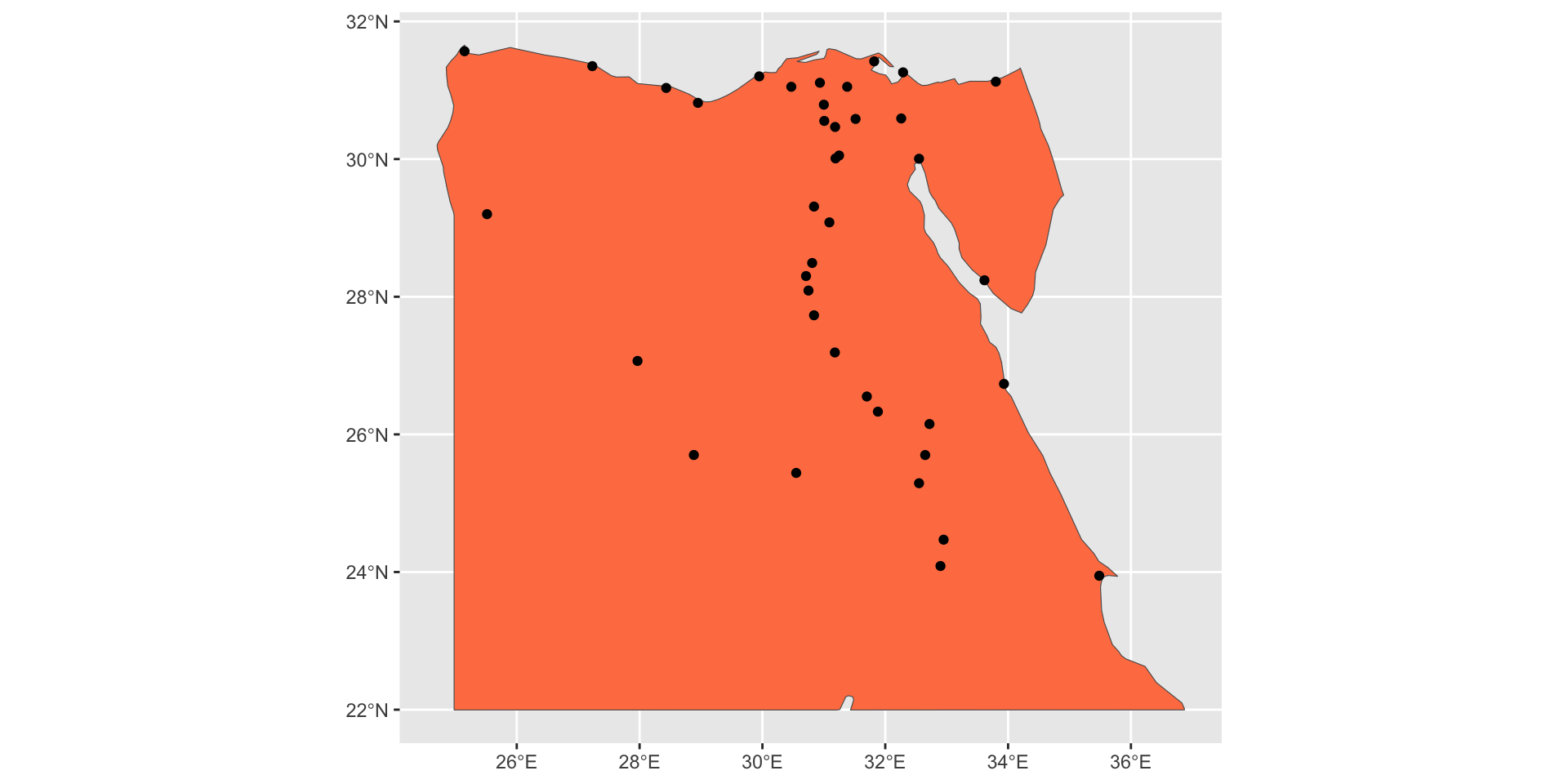
Кластерное распределение
Модели кластерных процессов работают в три этапа.
I. Генерируется “родительский” точечный процесс:
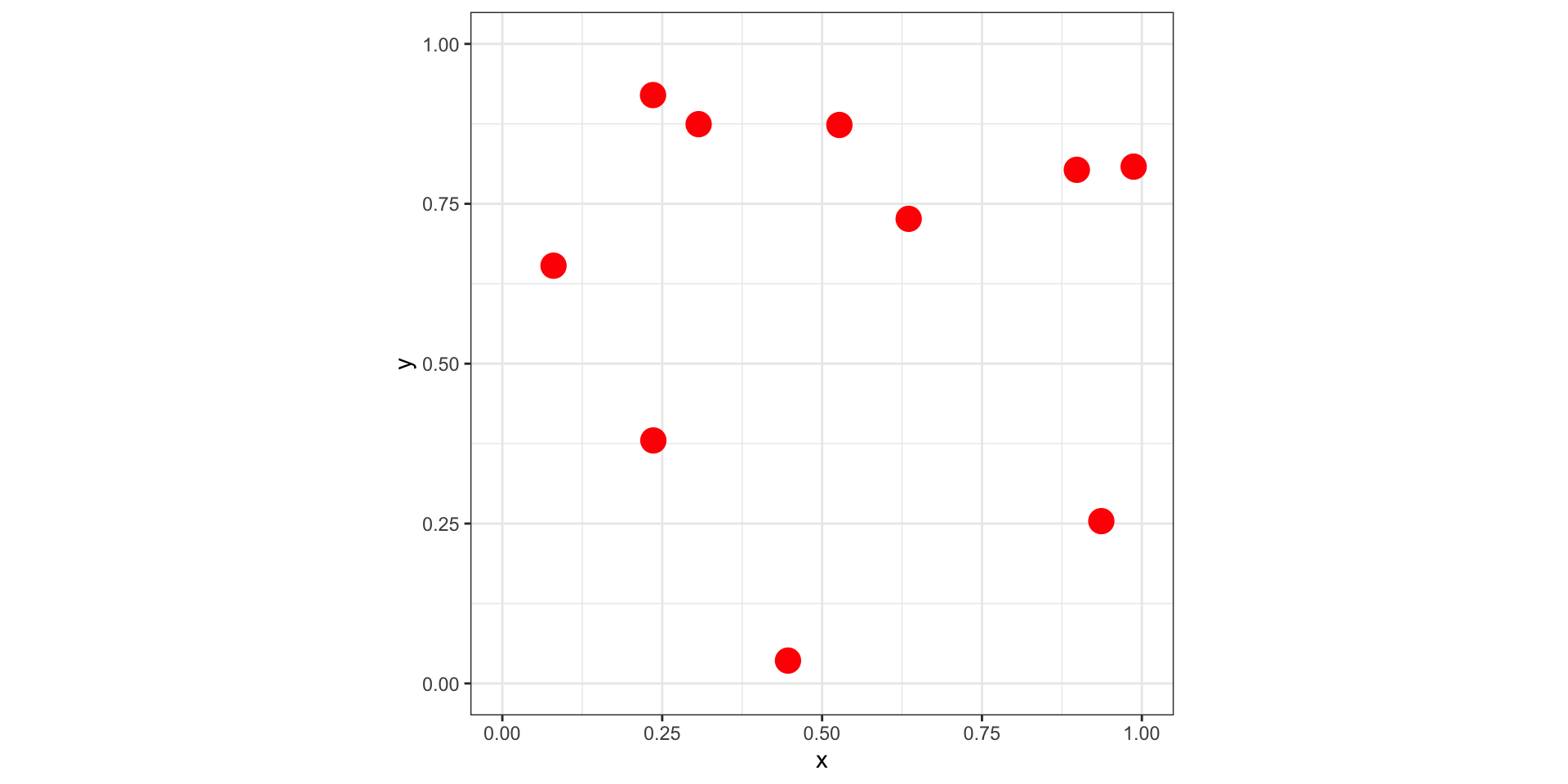
Кластерное распределение
Модели кластерных процессов работают в три этапа.
II. Относительно родителей генерируются потомки:
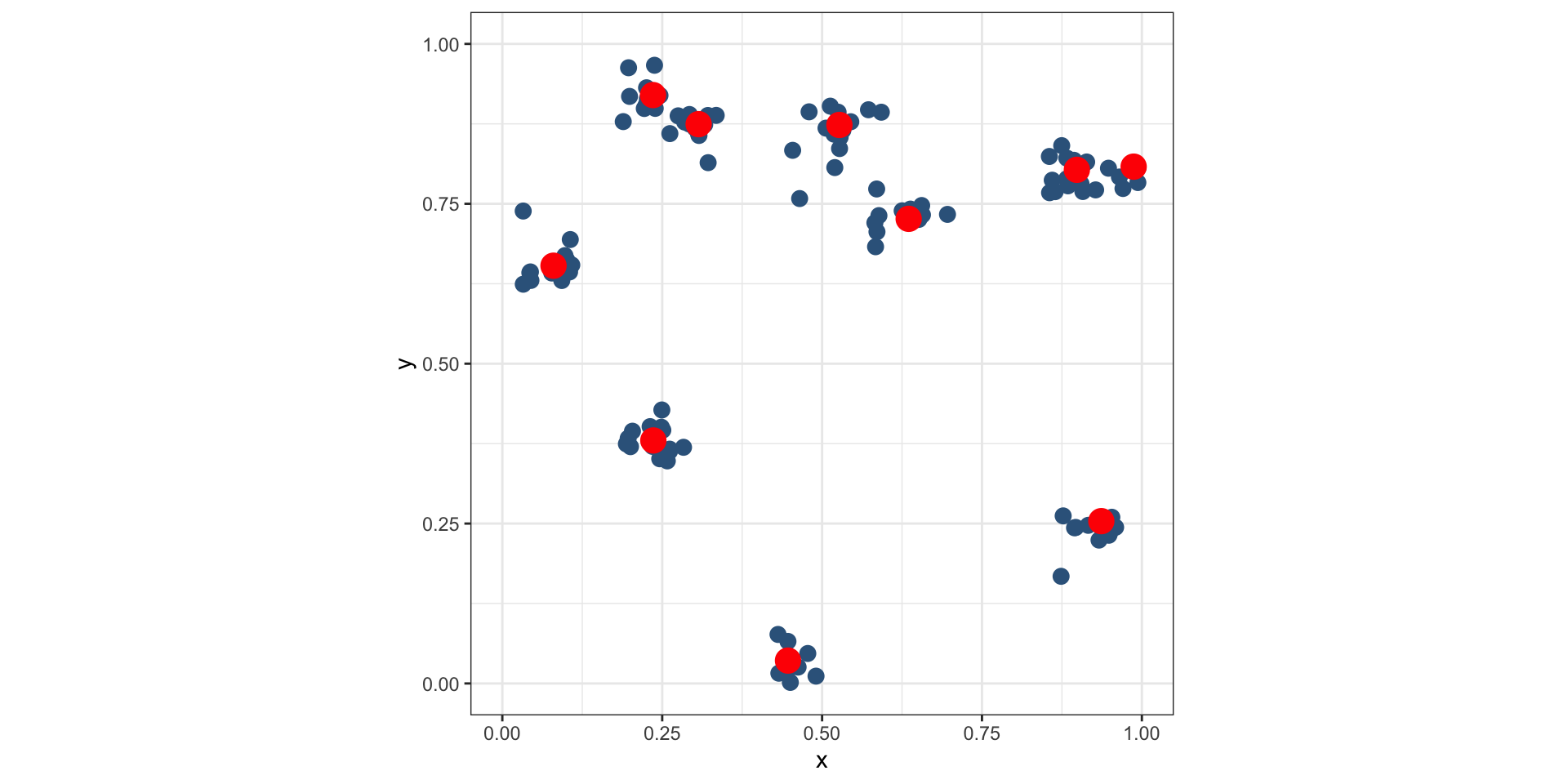
Кластерное распределение
Модели кластерных процессов работают в три этапа.
III. Родительские точки исключаются:
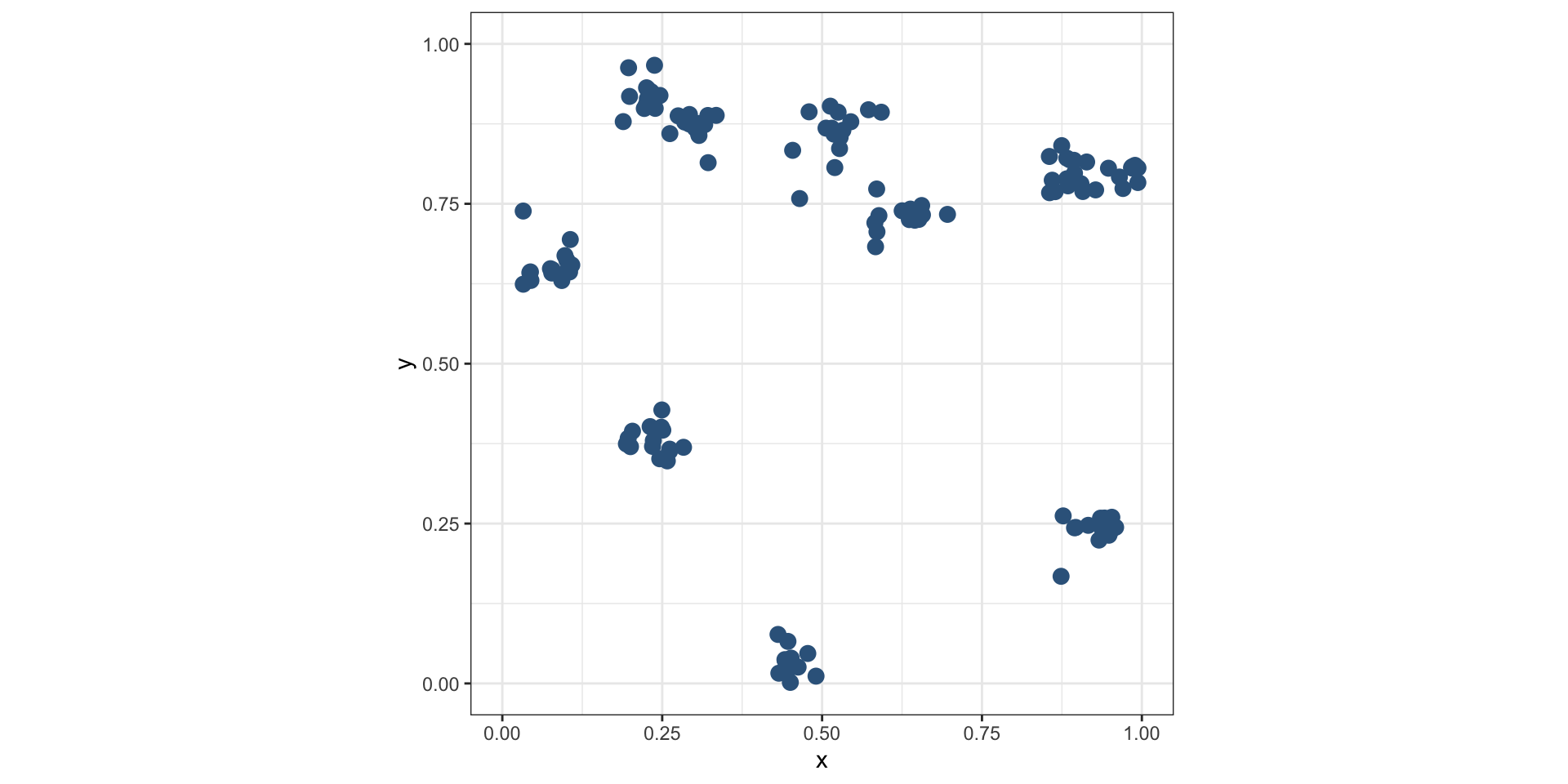
Кластерное распределение
Самая известная кластерная модель — Неймана-Скотта:
- Родительские точки — Пуассоновский процесс.
- Внутри каждого кластера потомки распределены независимо друг от друга.
- Потомки из разных кластеров так же распределены независимо друг от друга
- Закон распределения потомков относительно центра кластера одинаков для всех кластеров.
Модель Неймана-Скотта
Модель Неймана-Скотта была разработана для описания звёздных скоплений, но нашла широкое применение за пределами астрономии, в том числе в географическом анализе.
Генерация потомков
Процесс Матерна \((\kappa, \mu, r)\)
\(\Pi(\mu)\) случайных точек, равномерно распределенных в радиусе \(r\) относительно \(\Pi(\kappa)\) родительских точек
Потомки образуют однородные Пуассоновские процессы в окрестностях родителей.
У полученных кластеров четкие края — за пределами радиуса \(r\) потомков не бывает. По этой причине процесс также называется hardcore.
Генерация потомков
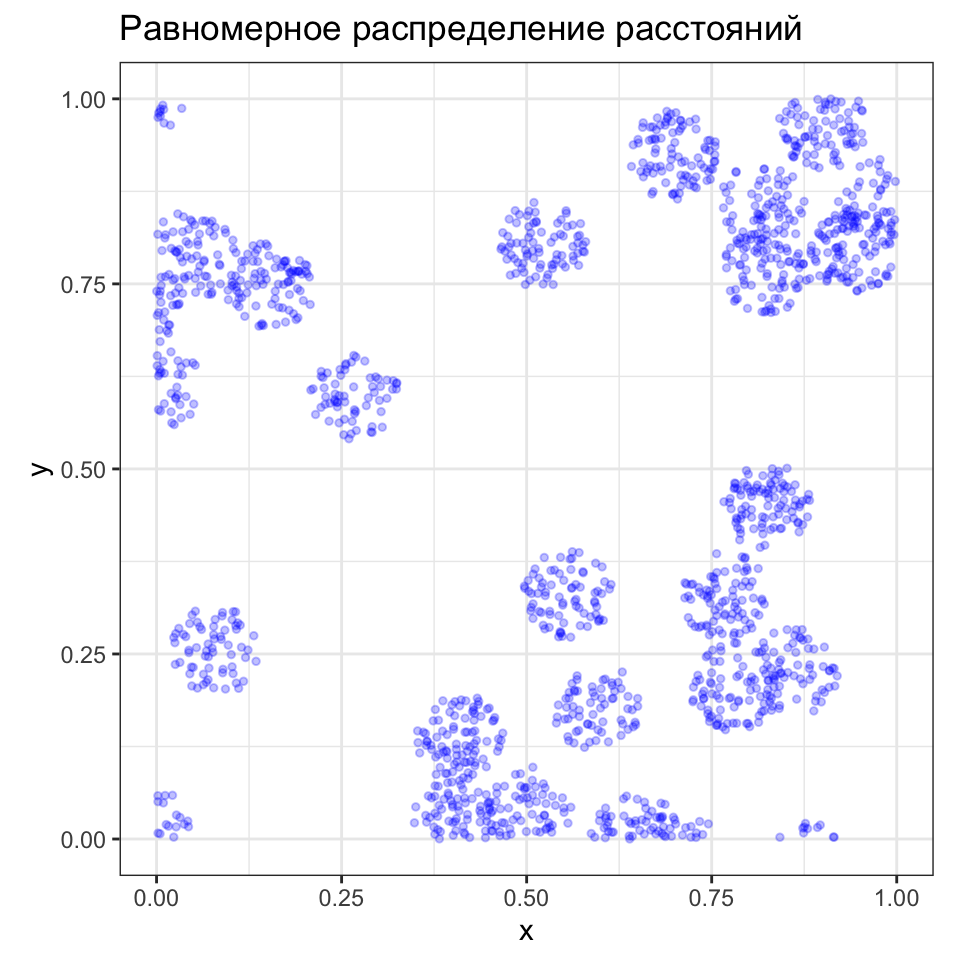
Процесс Томаса \((\kappa, \mu, \sigma)\)
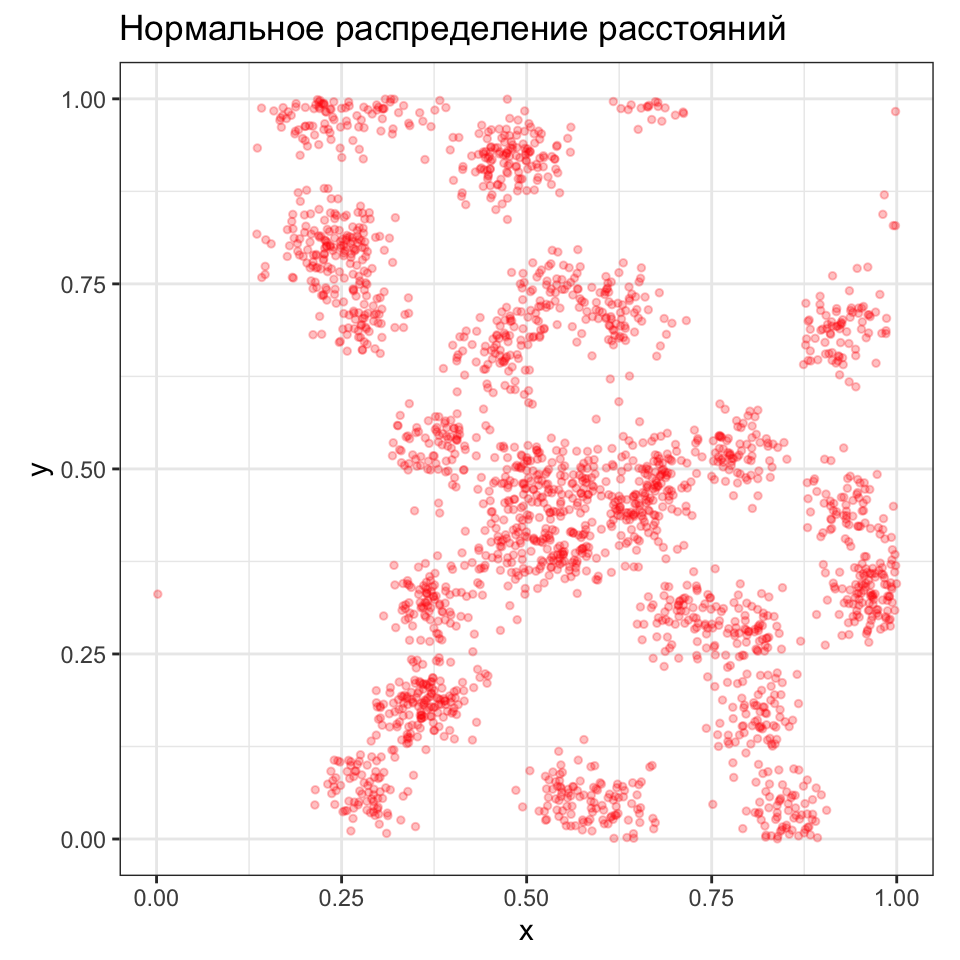
\(\Pi(\mu)\) случайных точек, расстояния которых относительно \(\Pi(\kappa)\) родительских точек распределены по нормальному закону \(N(0, \sigma^2)\)
Потомки образуют неоднородные Пуассоновские процессы — их плотность выше вблизи родителей
У полученных кластеров мягкие края — параметр \(\sigma\) определяет лишь среднеквадратическое отклонение расстояний
Регулярное распределение
Регулярным называется случайное распределение, при котором точки не могут располагаться ближе чем \(r\) — расстояние ингибиции.
Регулярное ≠ равномерное
Не следует путать регулярное распределение с равномерным. Равномерность означает постоянную плотность распределения.
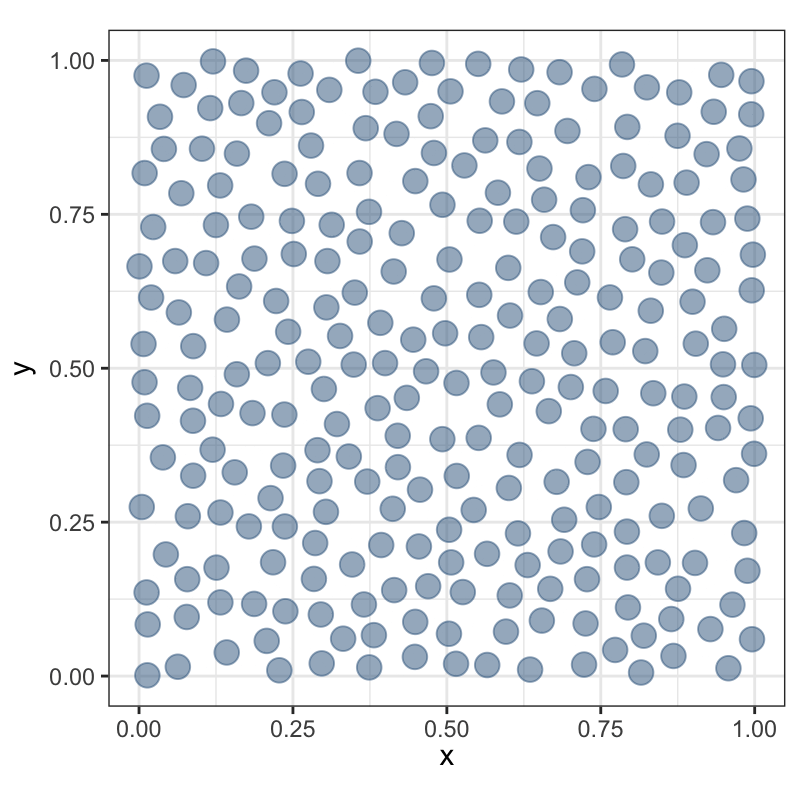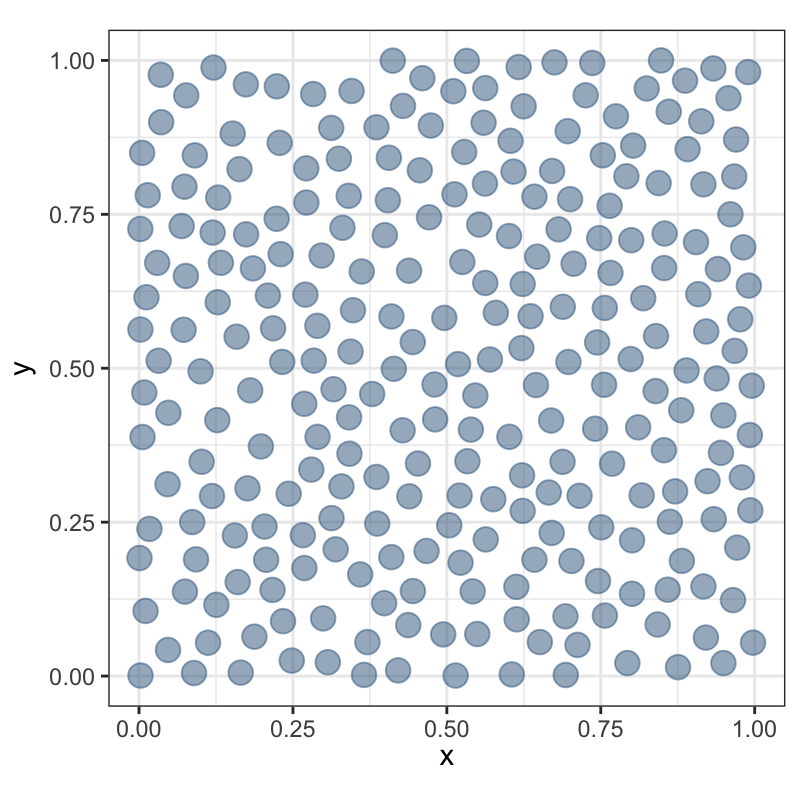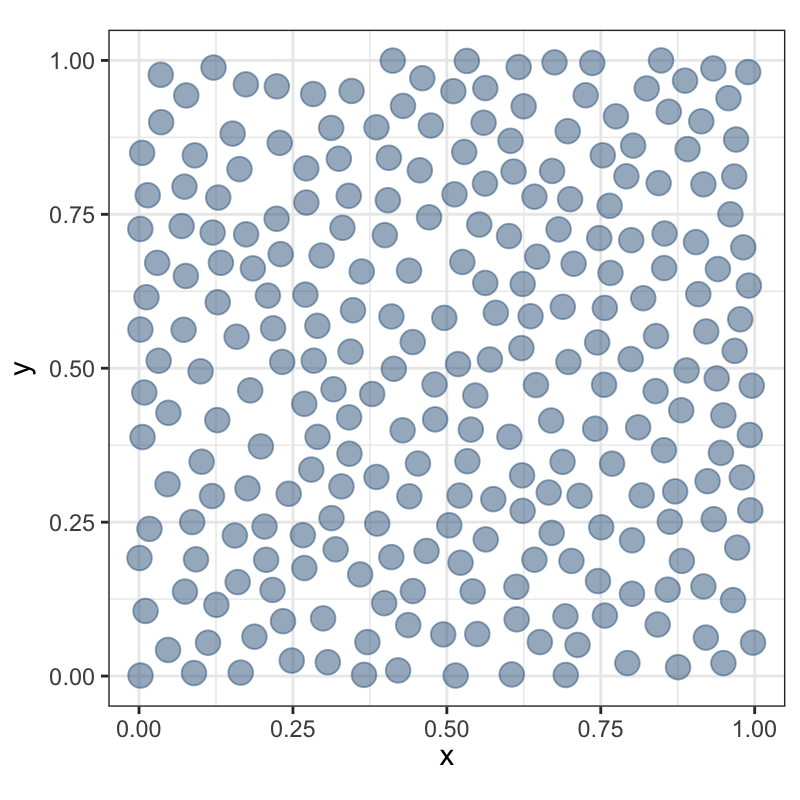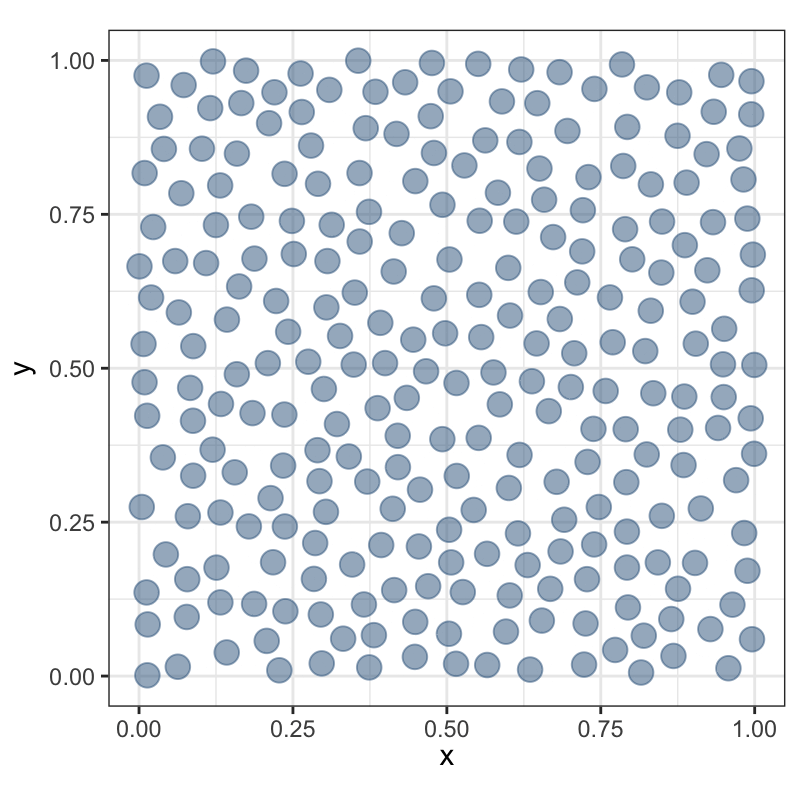
Причины
Регулярность распределения обычно свидетельствует о конкуренции за пространство и часто встречается в животном мире.
Генерация регулярного паттерна
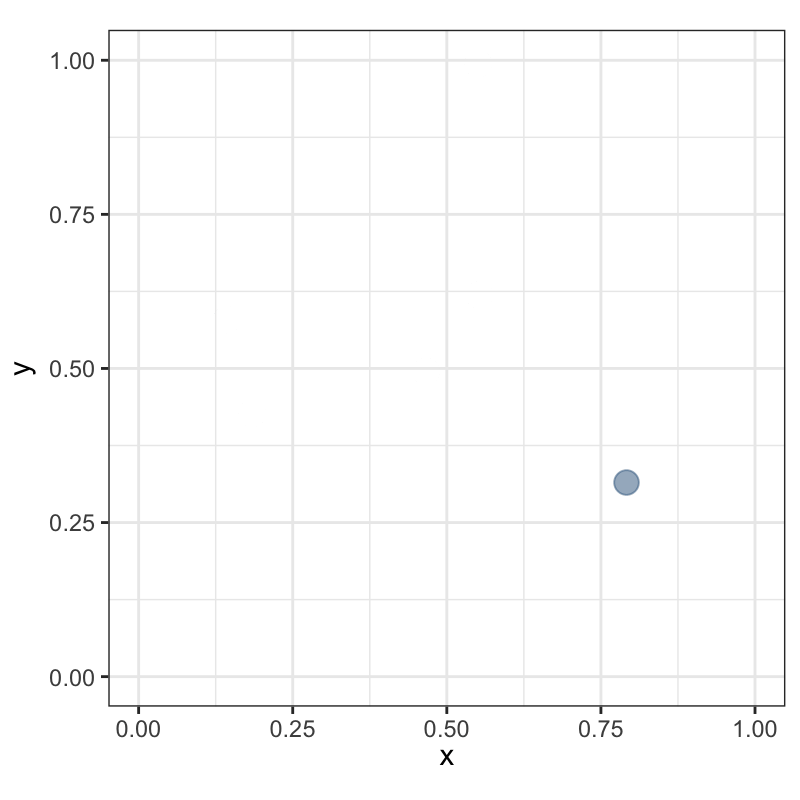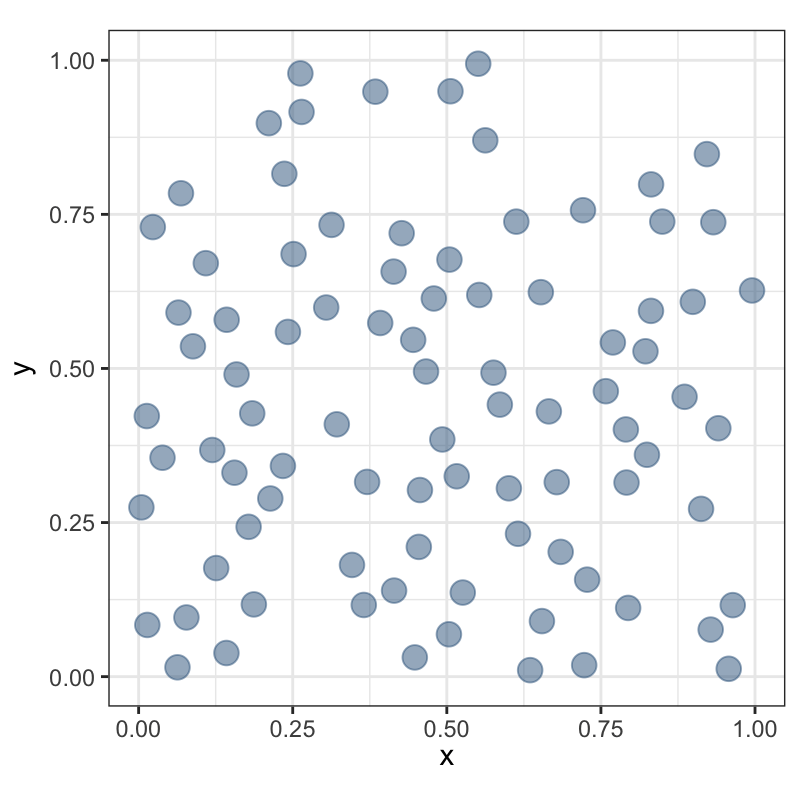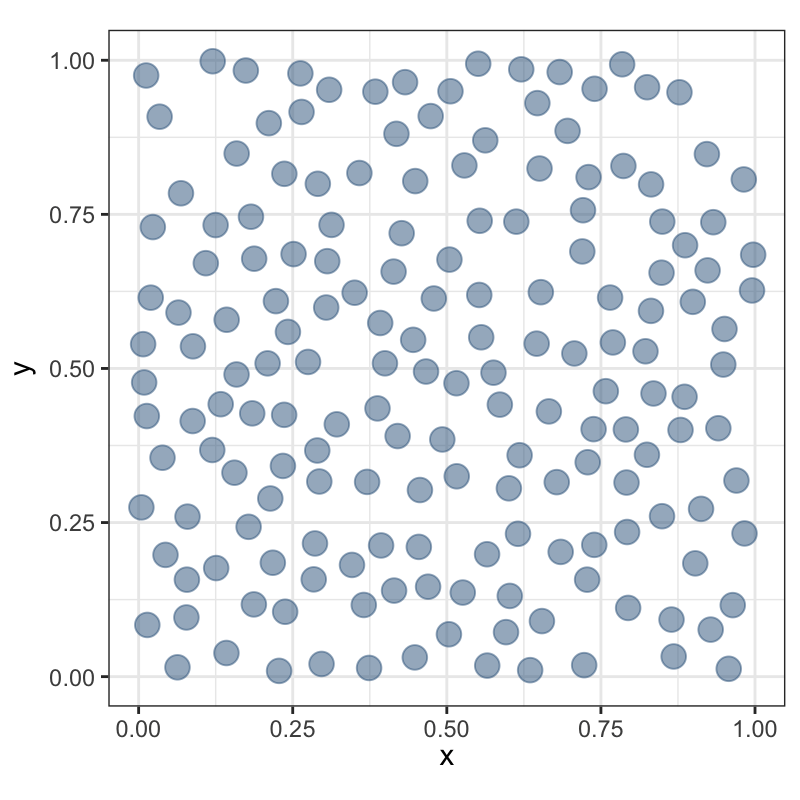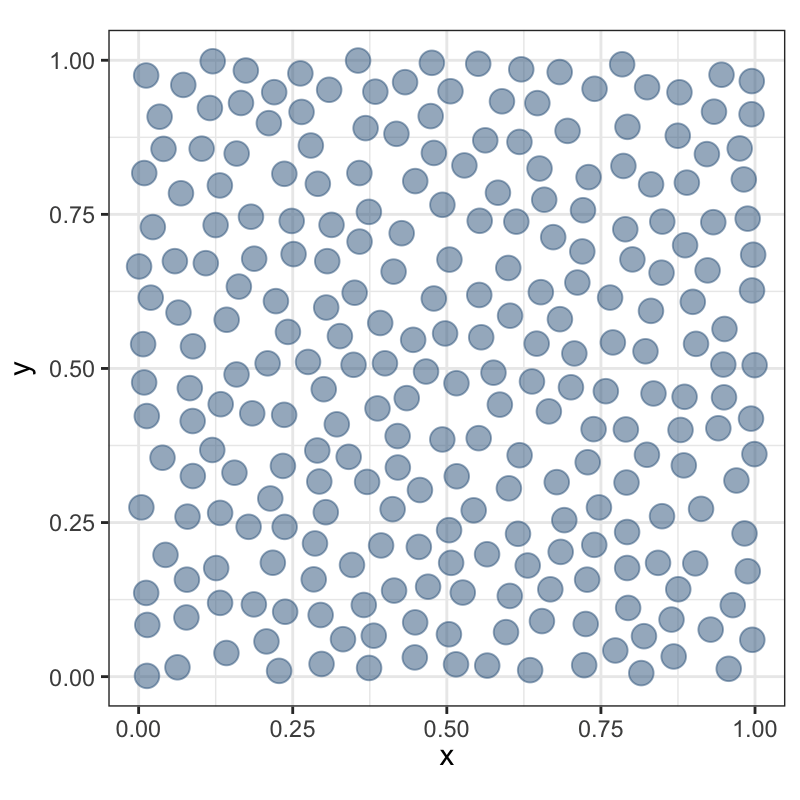
Последовательная модель:
генерировать абсолютно случайные (пуассоновские) точки по одной;
каждую последующую сохранять, если она находится на расстоянии не ближе \(r\) от сохраненных ранее.
Внимание
Процесс может не завершиться, если при высокой интенсивности задано также слишком большое расстояние ингибиции. В этом случае будет недостаточно места для размещения ожидаемого числа точек.
Диагностика распределений
Выявление типа распределения осуществляется на основе статистических тестов применительно к свойствам двух типов
Свойства I порядка
Оценивается интенсивность точечного процесса \(\lambda\) , ее статистическое распределение
плотность пространственного распределения;
количество точек по ячейкам регулярной сетки.
Свойства II порядка
Оцениваются расстояния между точками, их статистическое распределение
расстояние до ближайшего соседа;
расстояние до \(K\) ближайших соседей (функция Рипли).
Плотность распределения
Оценка плотности пространственного распределения делается методом ядерного сглаживания.
Над каждой точкой позиционируется ядро — мини-поверхность:
Плотность распределения
Оценка плотности пространственного распределения делается методом ядерного сглаживания.
Сумма поверхностей дает оценку плотности в точке:
Плотность распределения
Однородный пуассоновский
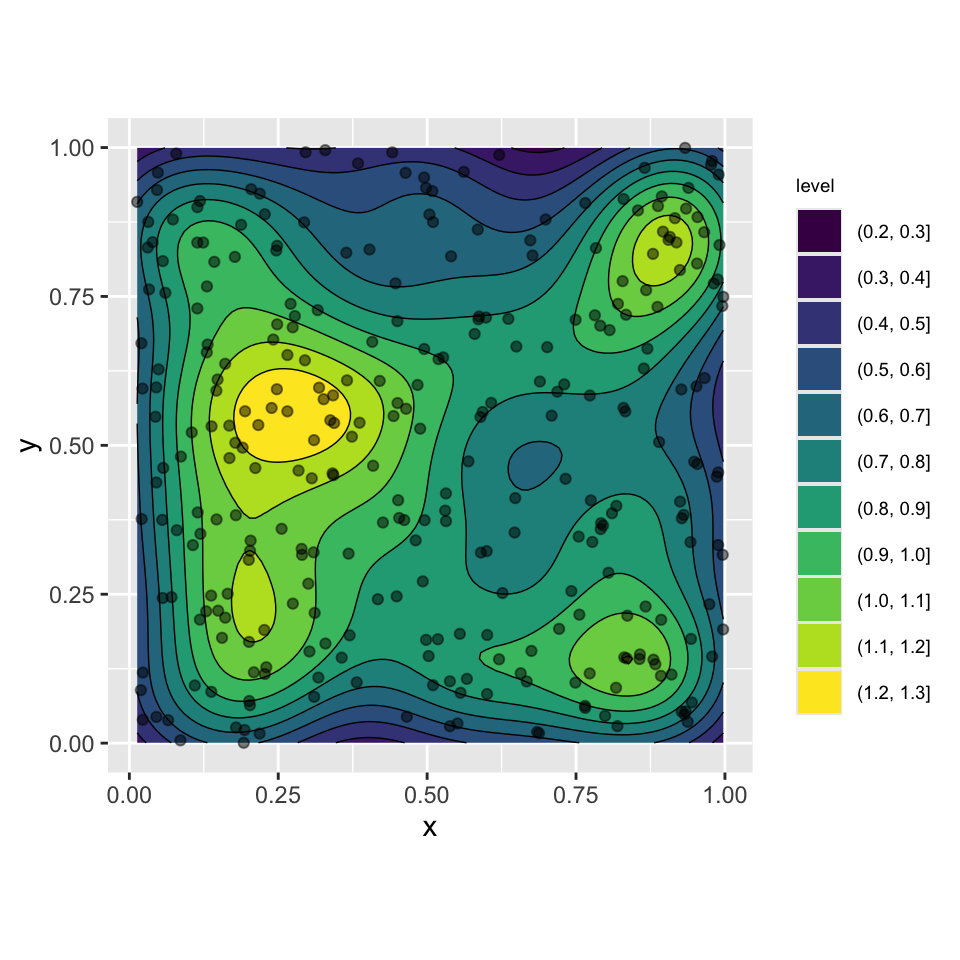
Неоднородный пуассоновский
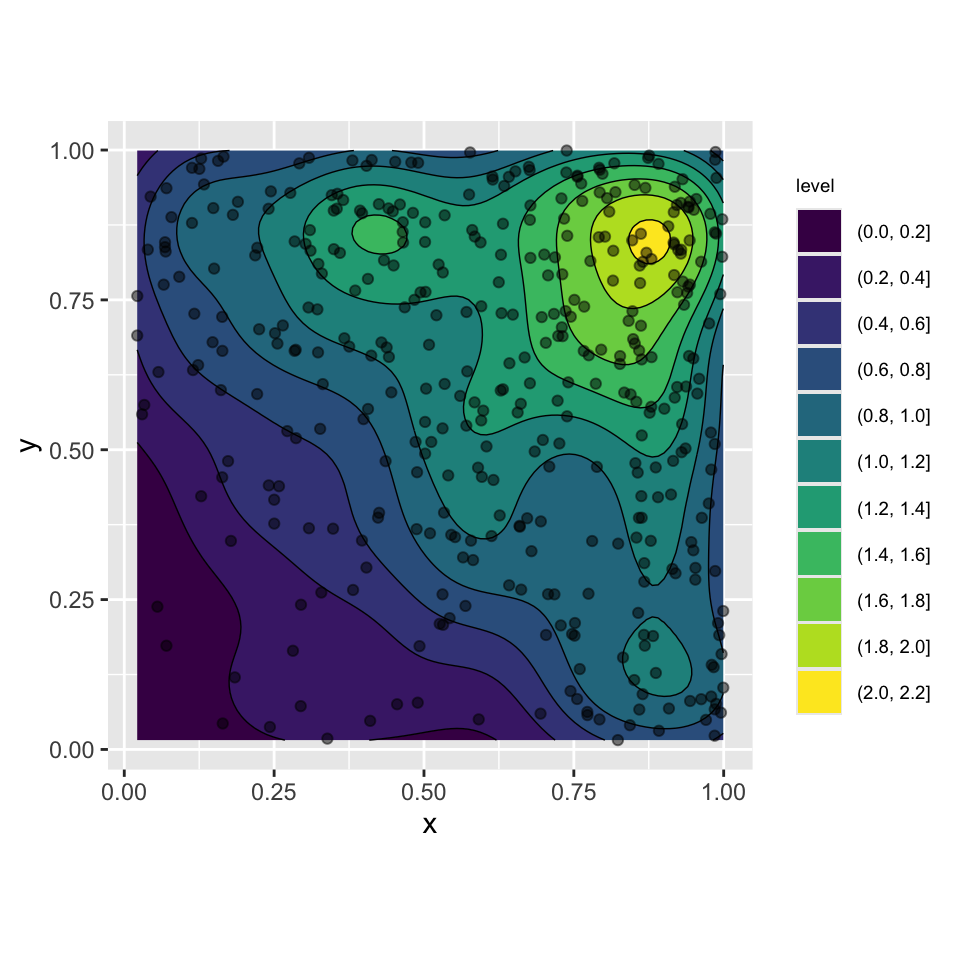
Плотность распределения
Кластерный Матерна
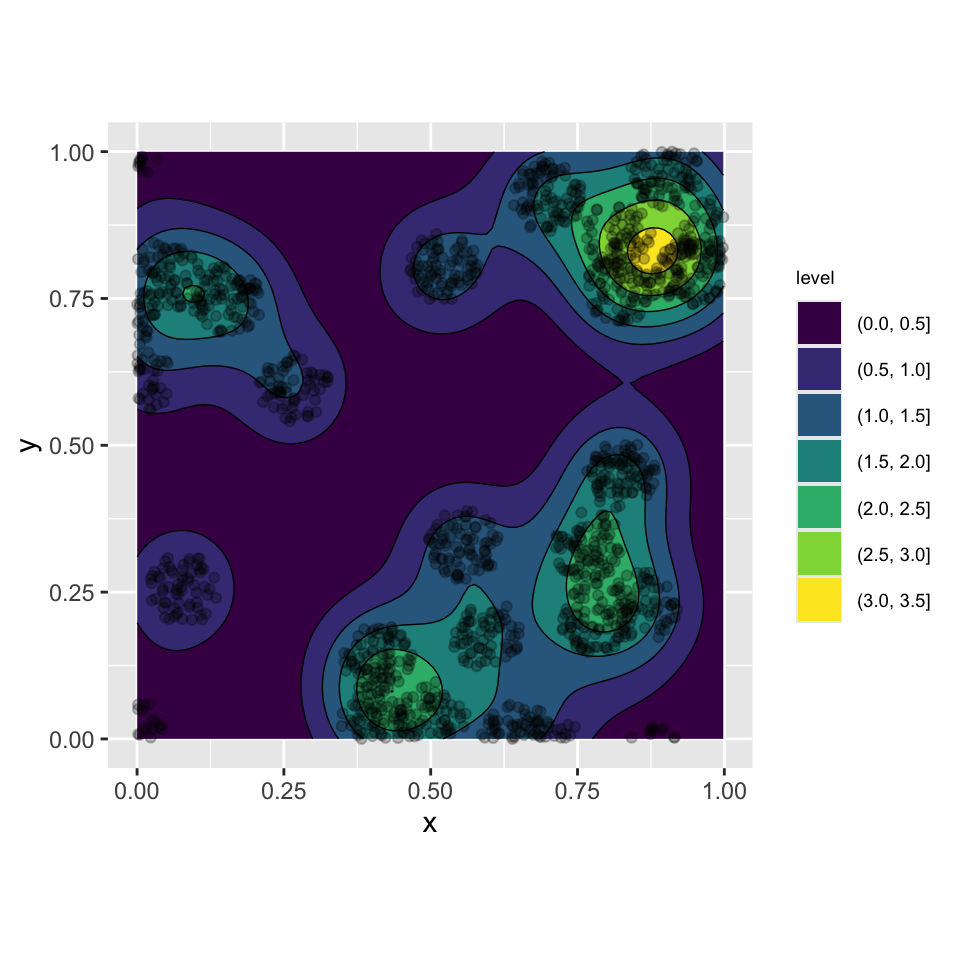
Кластерный Томаса
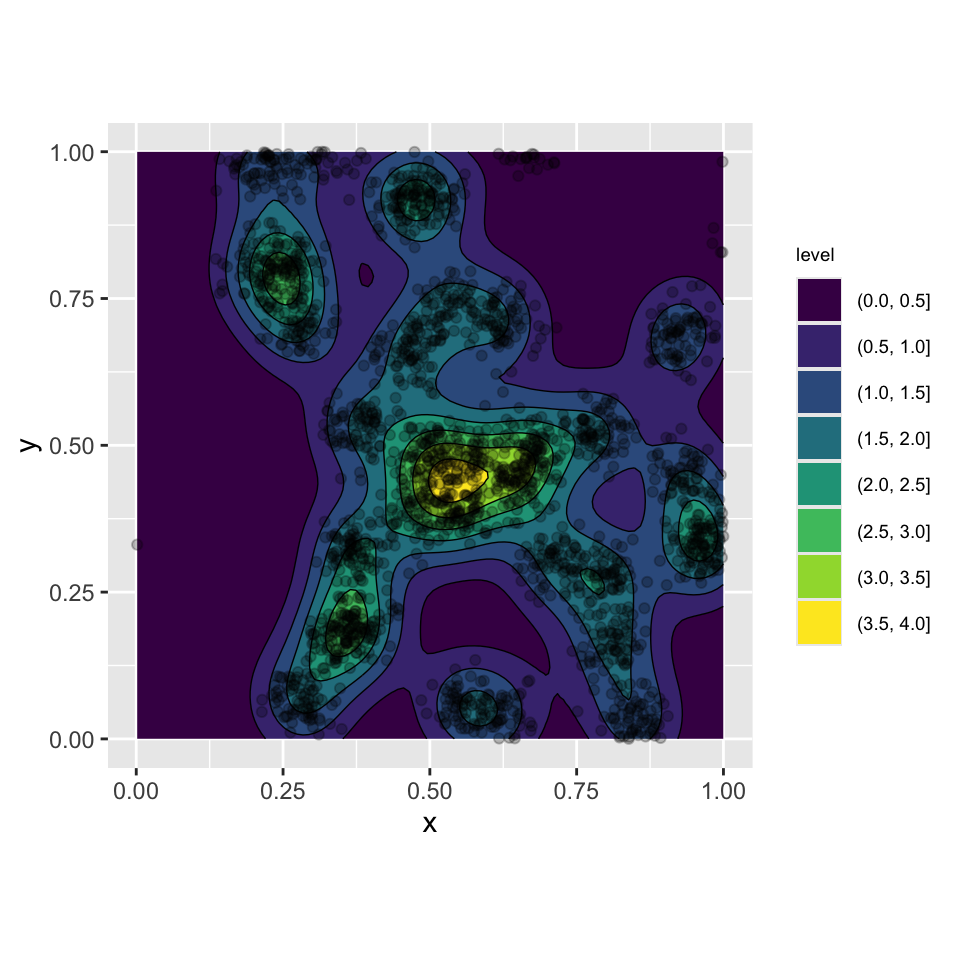
Плотность распределения
Диагностика плотности
- Чем выше разброс значений плотности распределения, тем сильнее оно отличается от регулярного.
- При оценке плотности могут возникать краевые эффекты, связанные с тем, что вблизи границ располагается меньшее число точек
Регулярный
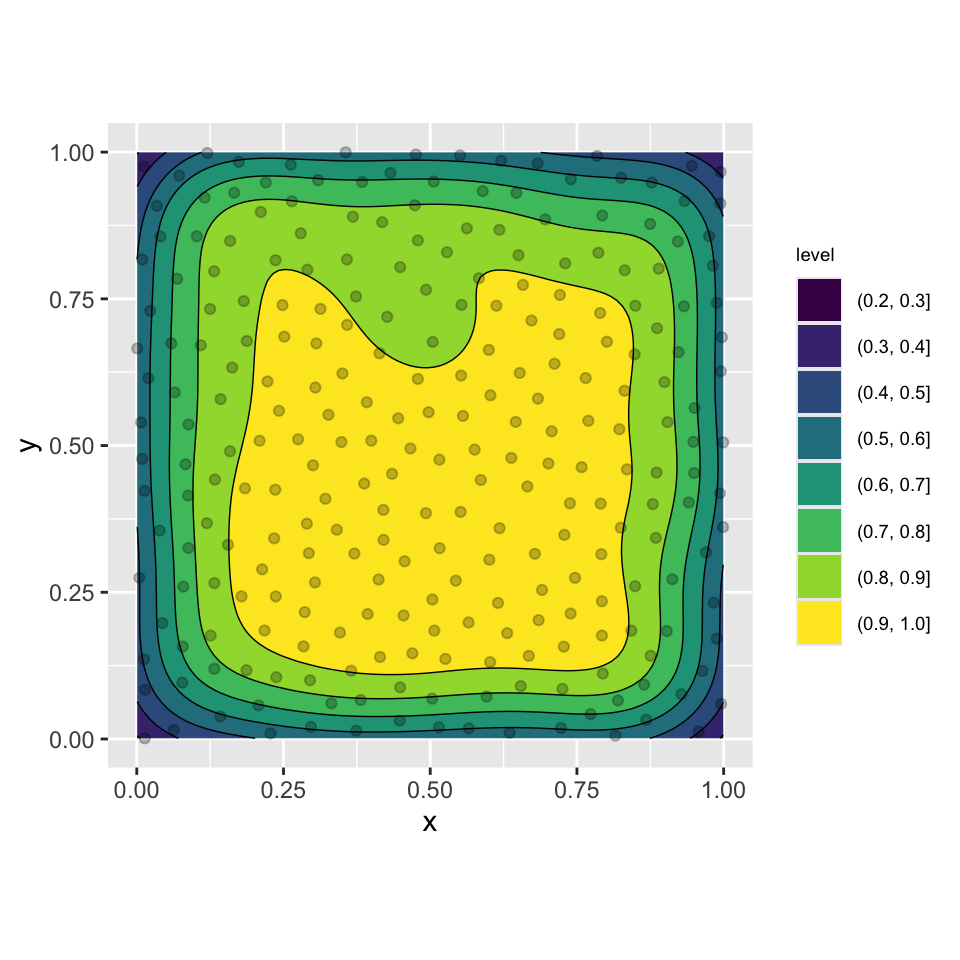
G-функция
\(G\)-функция — эмпирическая функция распределения расстояний до ближайшего соседа:
\[ G(r) = \frac{1}{n}\sum_{i=1}^n \big[r_{min}(p_i) < r \big], \]
\(r_{min}\) — расстояние от \(p_i\) до ближайшей к ней точки.
\([~\circ~]\) — индикаторная функция, принимающая значения:
\(1\), если \(\circ = ИСТИНА\),
\(0\), если \(\circ = ЛОЖЬ\).
G-функция
Чтобы понять тип распределения, необходимо сравнить \(G\)-функцию для фактического распределения с \(G\)-функцией, которую имел бы абсолютно случайный паттерн на той же территории при том же количестве точек
- По фактическим данным оценивается интенсивность процесса \(\lambda\).
- Осуществляется множество симуляций пуассоновского процесса с интенсивностью \(\lambda\).
- Для каждого значения \(r\) находят среднюю величину \(G(r)\), а также разброс \(\pm 3\sigma\) по множеству симуляций.
- Полученные значения дают оценку ожидаемой \(G\)-функции и ее доверительного интервала для случайного распределения.
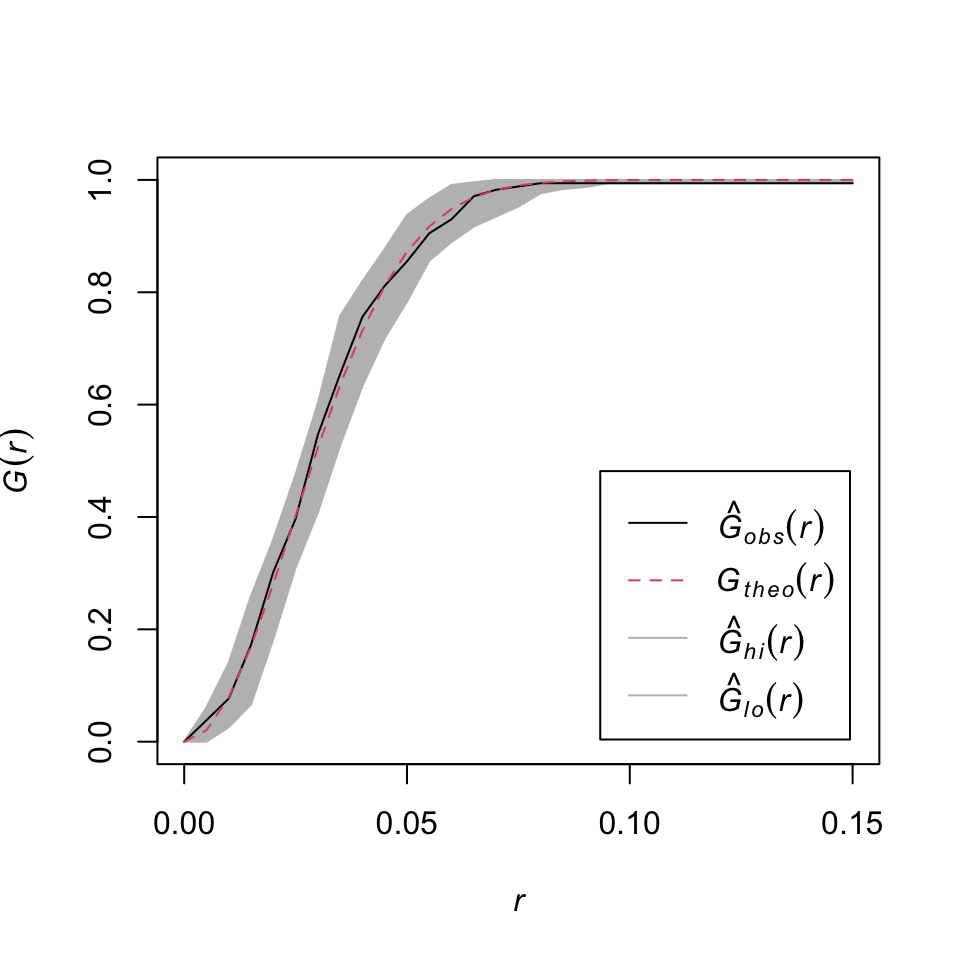
G-функция
Абсолютно случайное распределение
График фактического распределения \(\widehat G_{obs} (r)\) находится в пределах доверительного интервала относительно теоретического распределения \(G_{theo}(r)\).
Достоверных отличий нет.
G-функция
Кластерное распределение
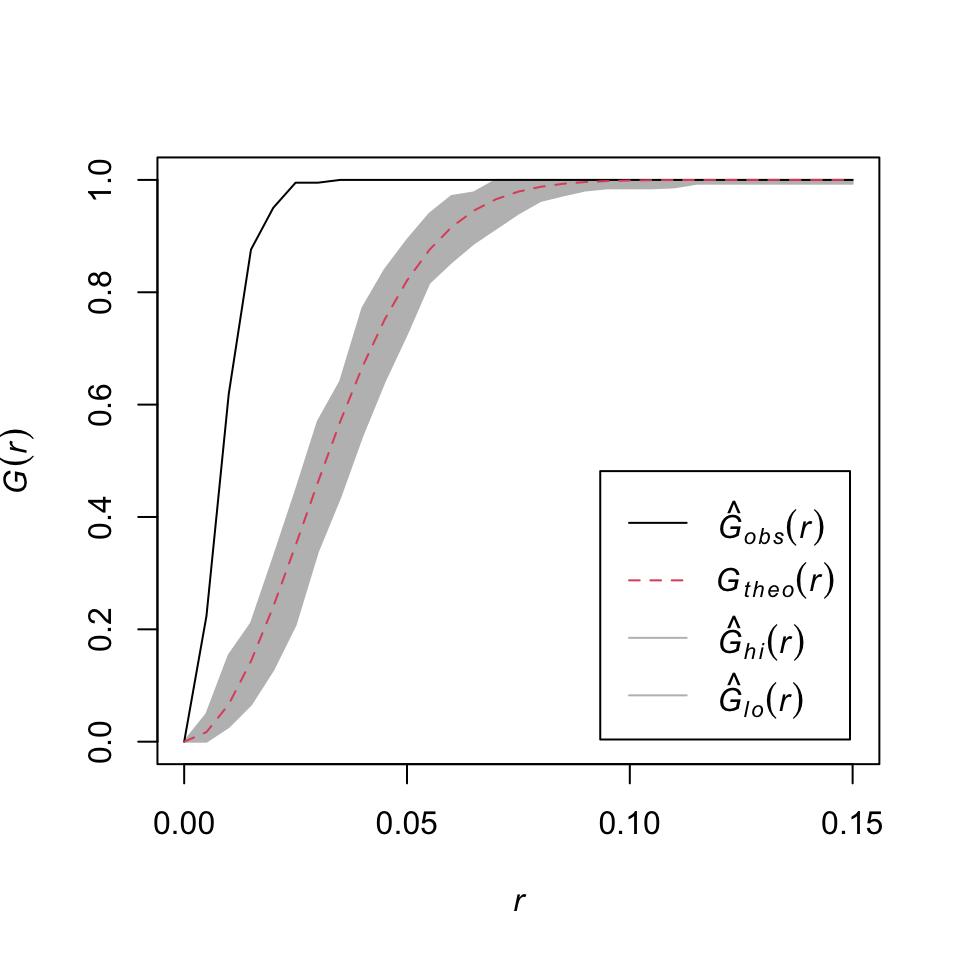
График фактического распределения \(\widehat G_{obs} (r)\) находится над графиком теоретического распределения \(G_{theo}(r)\).
Малые расстояния встречаются чаще, чем в пуассоновском процессе.
G-функция
Регулярное распределение
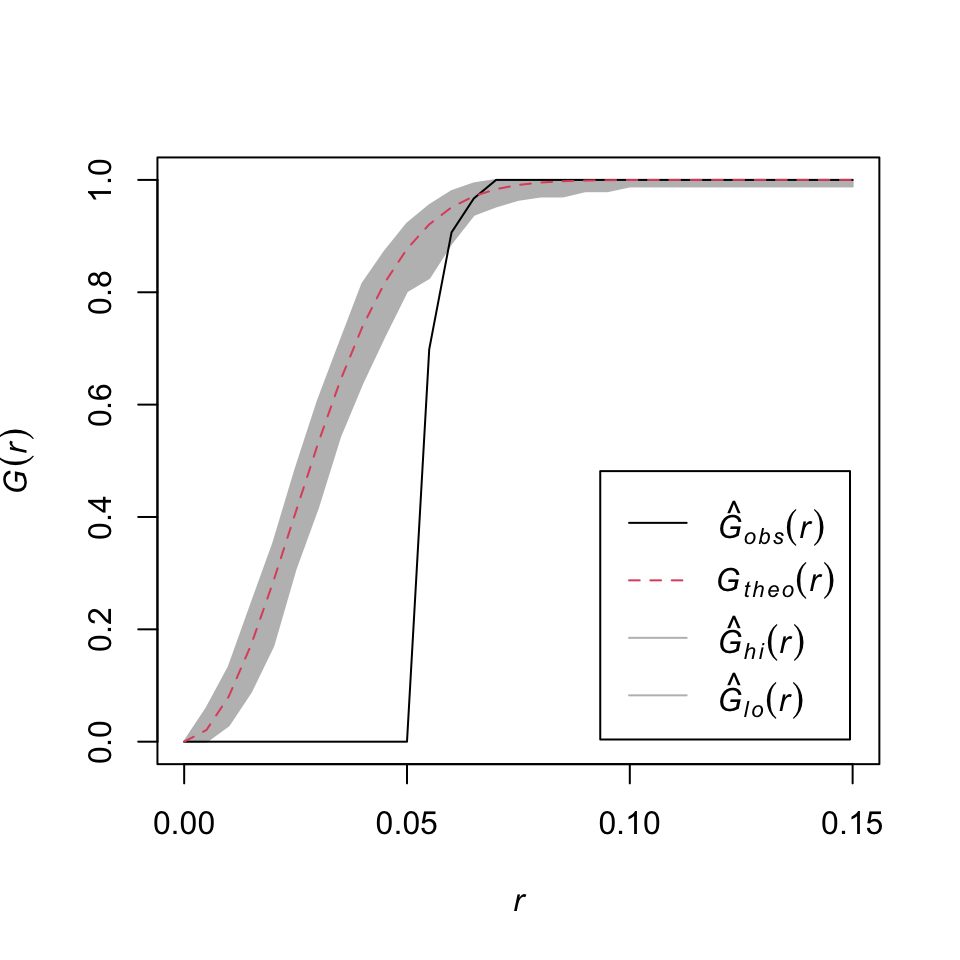
График фактического распределения \(\widehat G_{obs} (r)\) находится под графиком теоретического распределения \(G_{theo}(r)\).
Малые расстояния встречаются реже, чем в пуассоновском процессе.
Пример
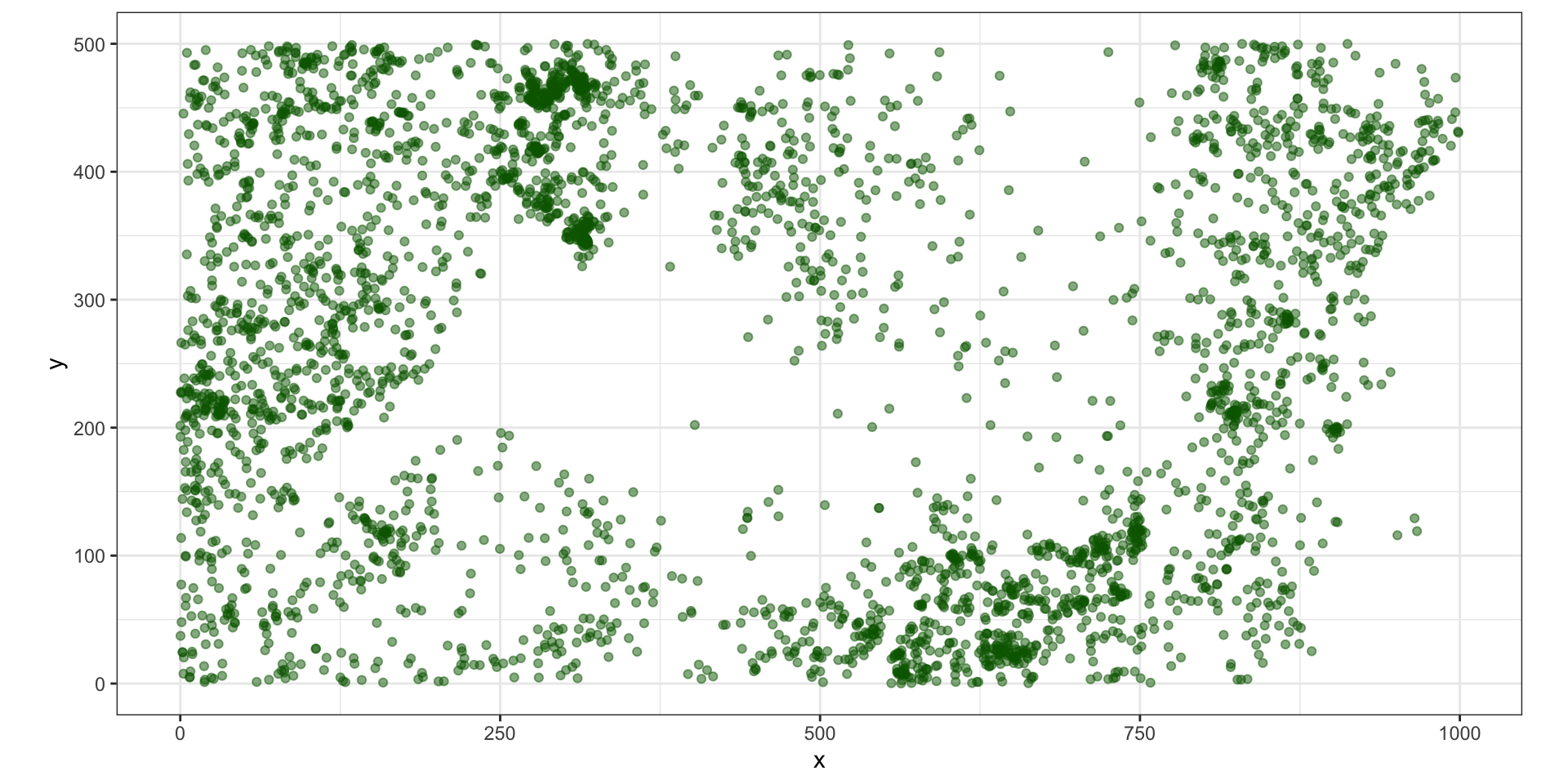
Рассмотрим данные по расположению деревьев во влажном тропическом лесу:
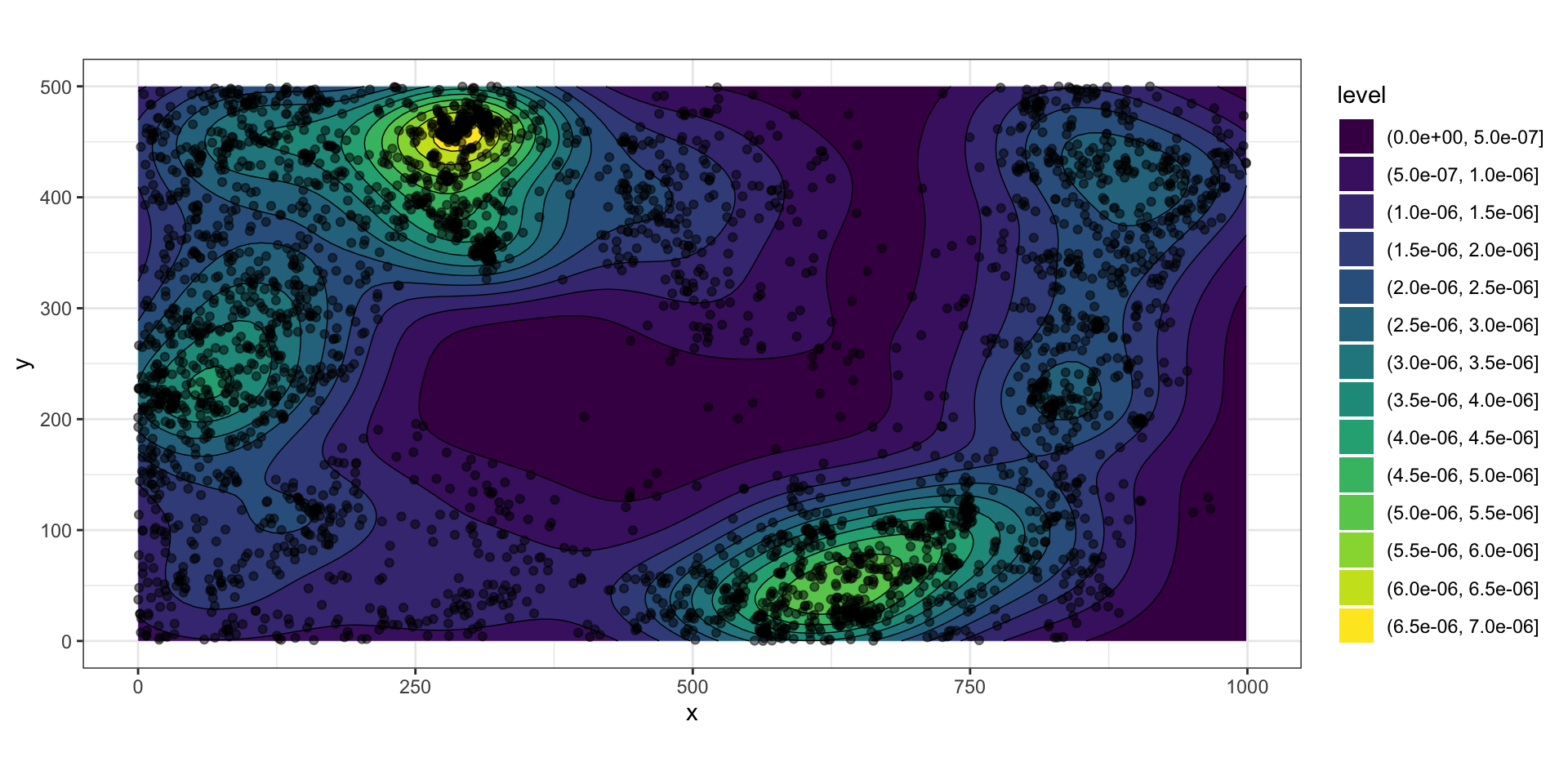
Плотность распределения
Характер плотности пространственного распределения говорит о неоднородном Пуассоновском процессе
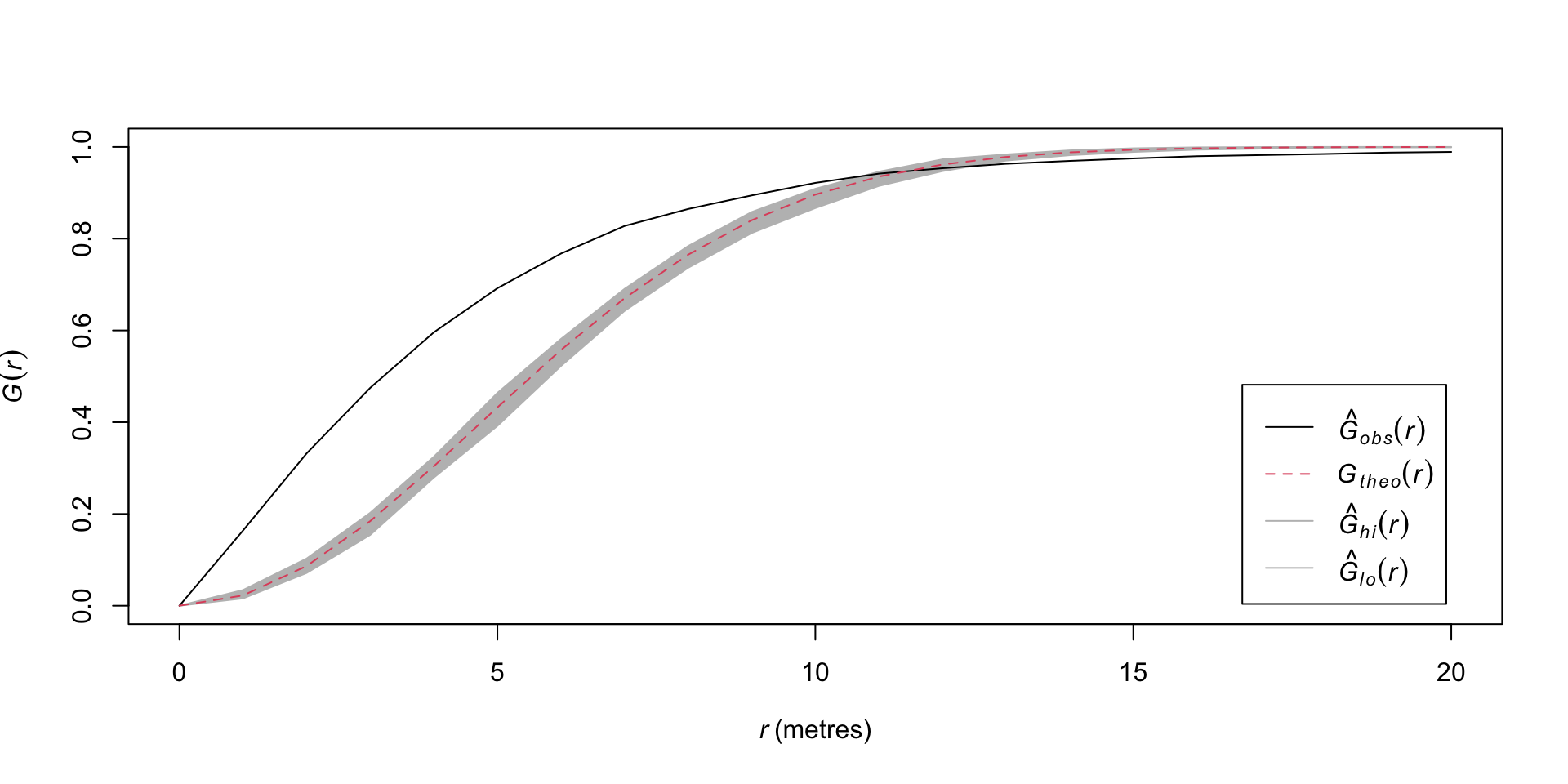
G-функция
Характер G-функции говорит о неоднородном Пуассоновском либо кластерном процессе
Высота рельефа
Можно связать функцию интенсивности с ковариатами — внешними факторами, такими как высота и уклон рельефа.

Уклон
Можно связать функцию интенсивности с ковариатами — внешними факторами, такими как высота и уклон рельефа.

Оценка интенсивности
Интенсивность процесса как функция от уклона
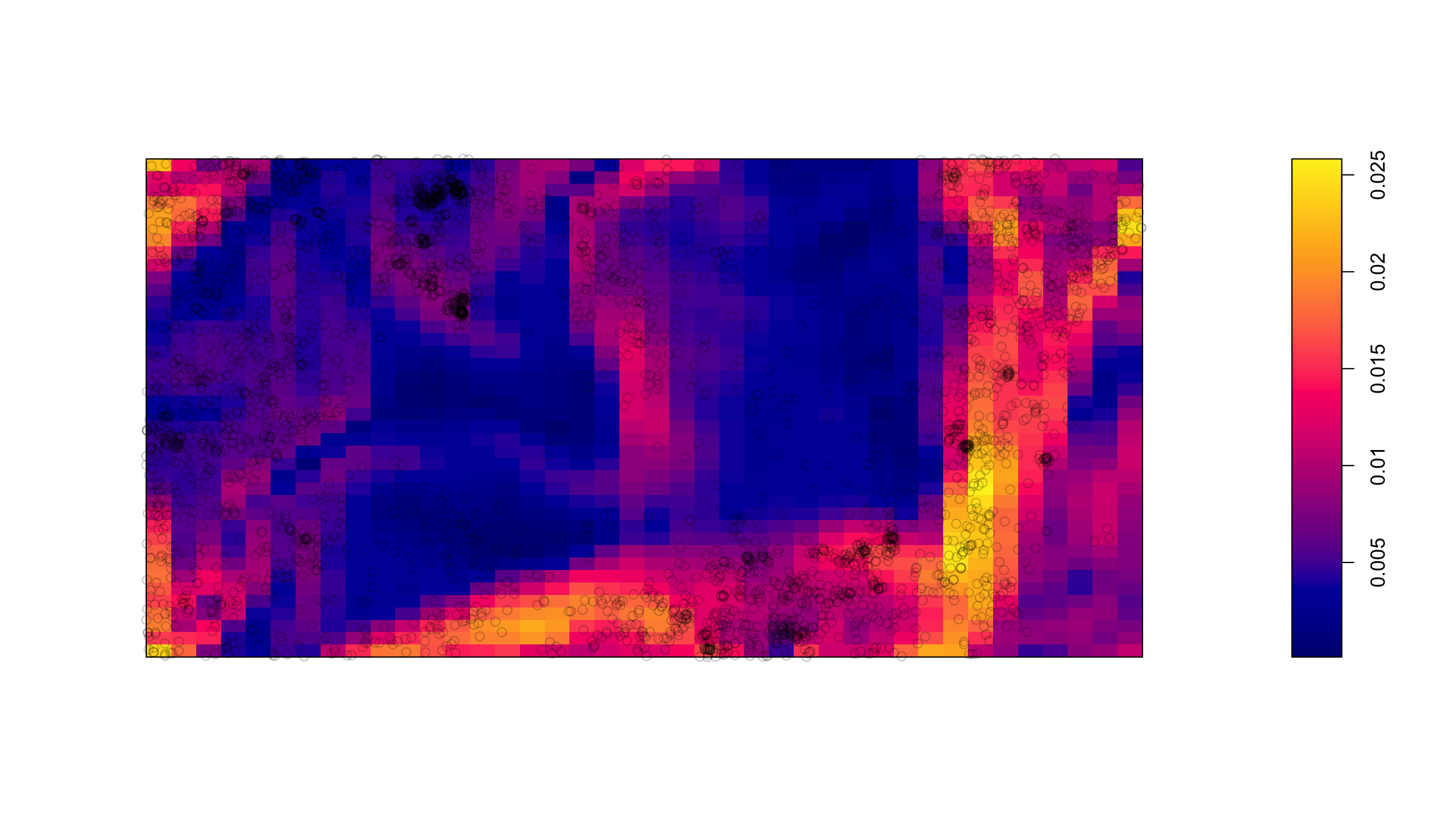
Моделирование
Методом Льюиса-Шедлера можно смоделировать альтернативные конфигурации неоднородного процесса:
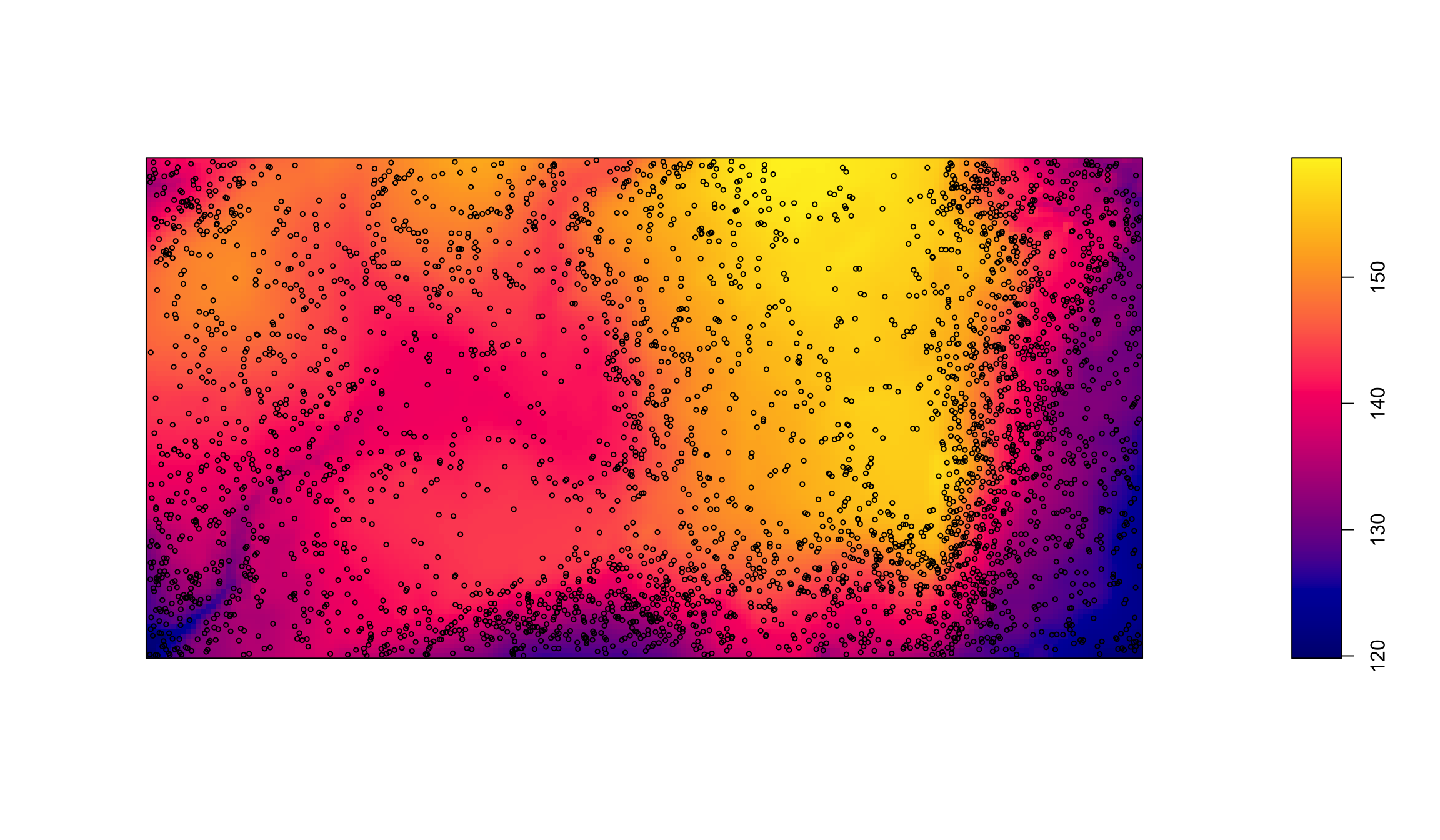
Моделирование
Методом Льюиса-Шедлера можно смоделировать альтернативные конфигурации неоднородного процесса:
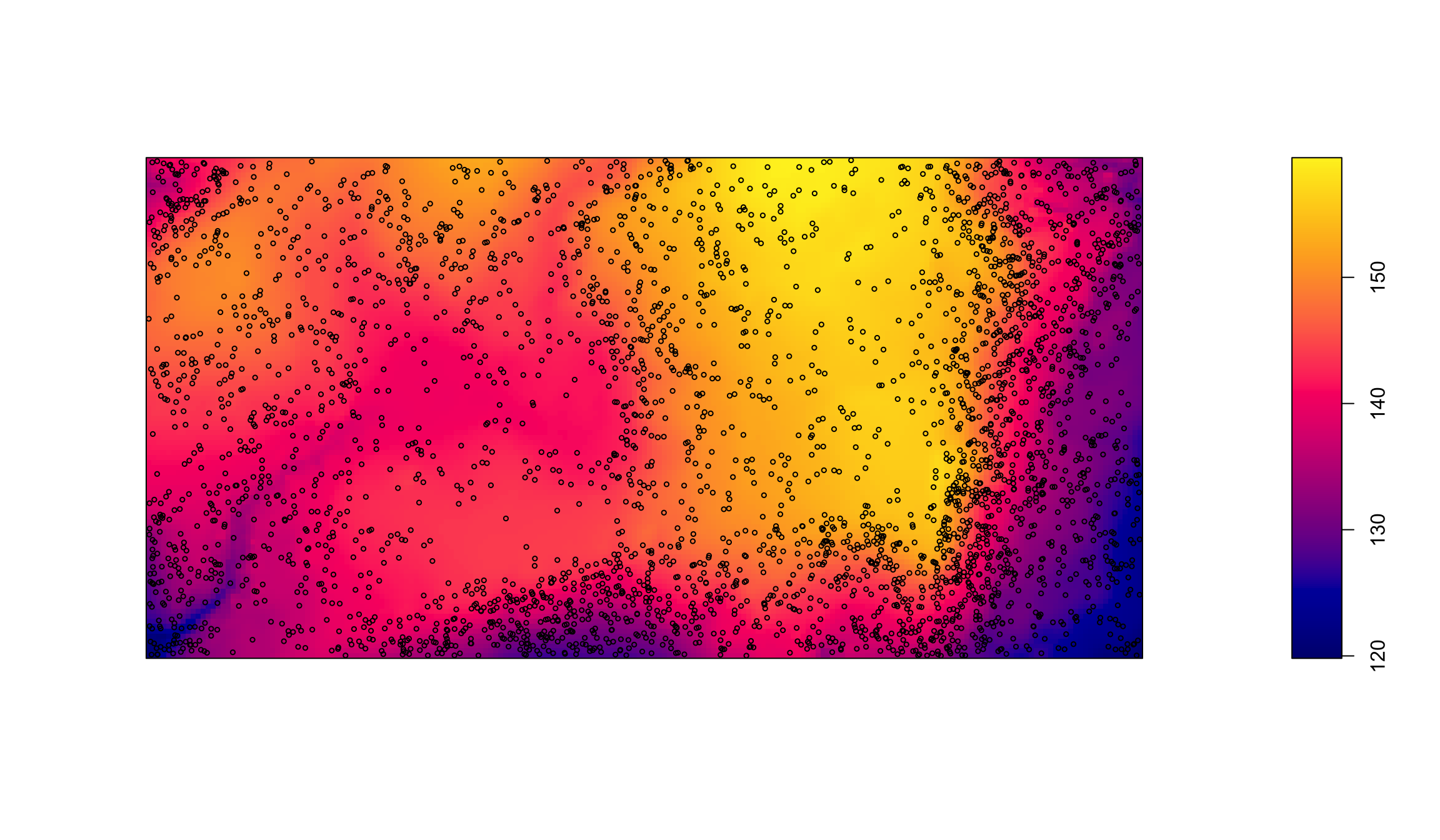
Моделирование
Методом Льюиса-Шедлера можно смоделировать альтернативные конфигурации неоднородного процесса:
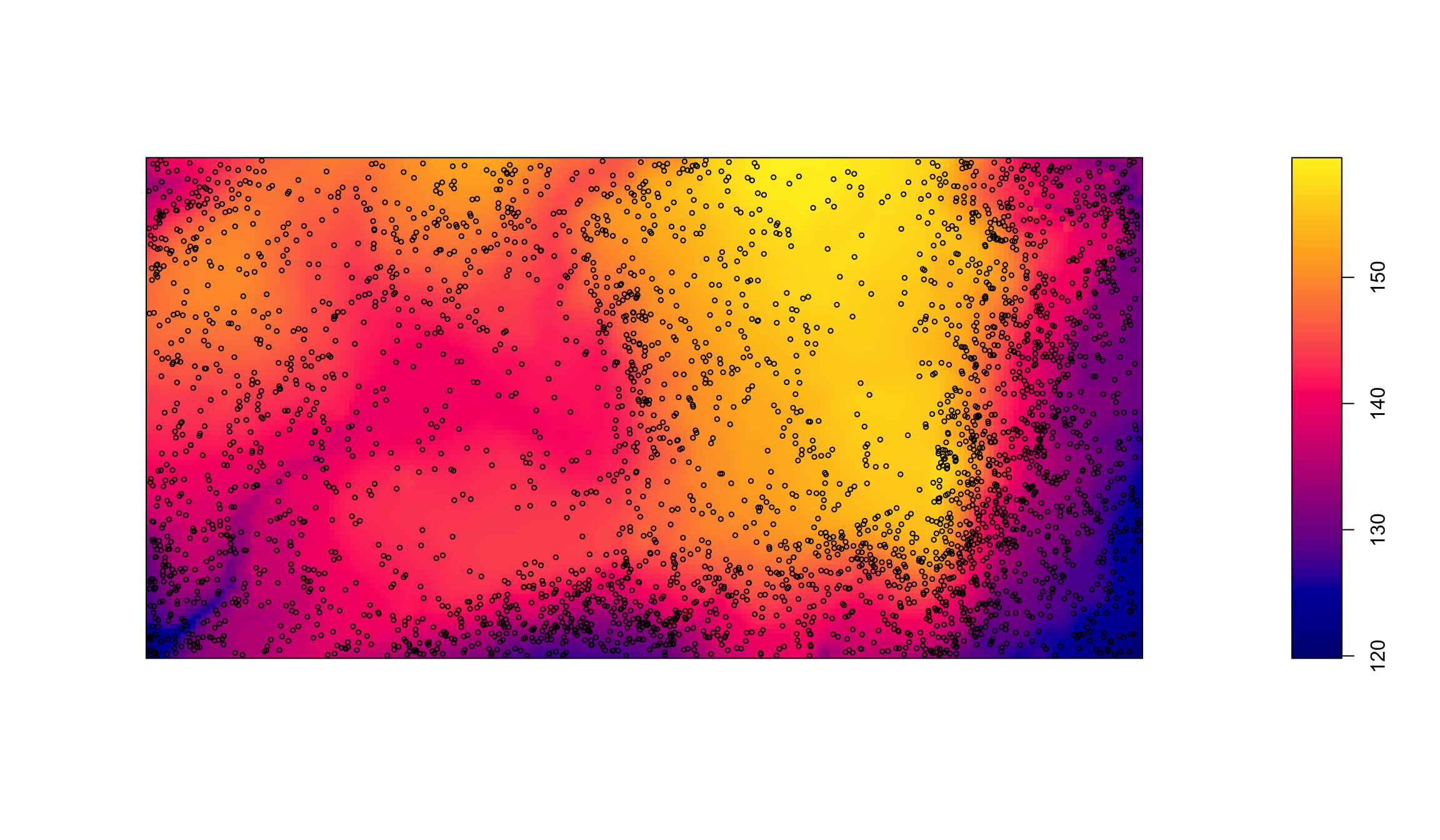
Моделирование
Методом Льюиса-Шедлера можно смоделировать альтернативные конфигурации неоднородного процесса:
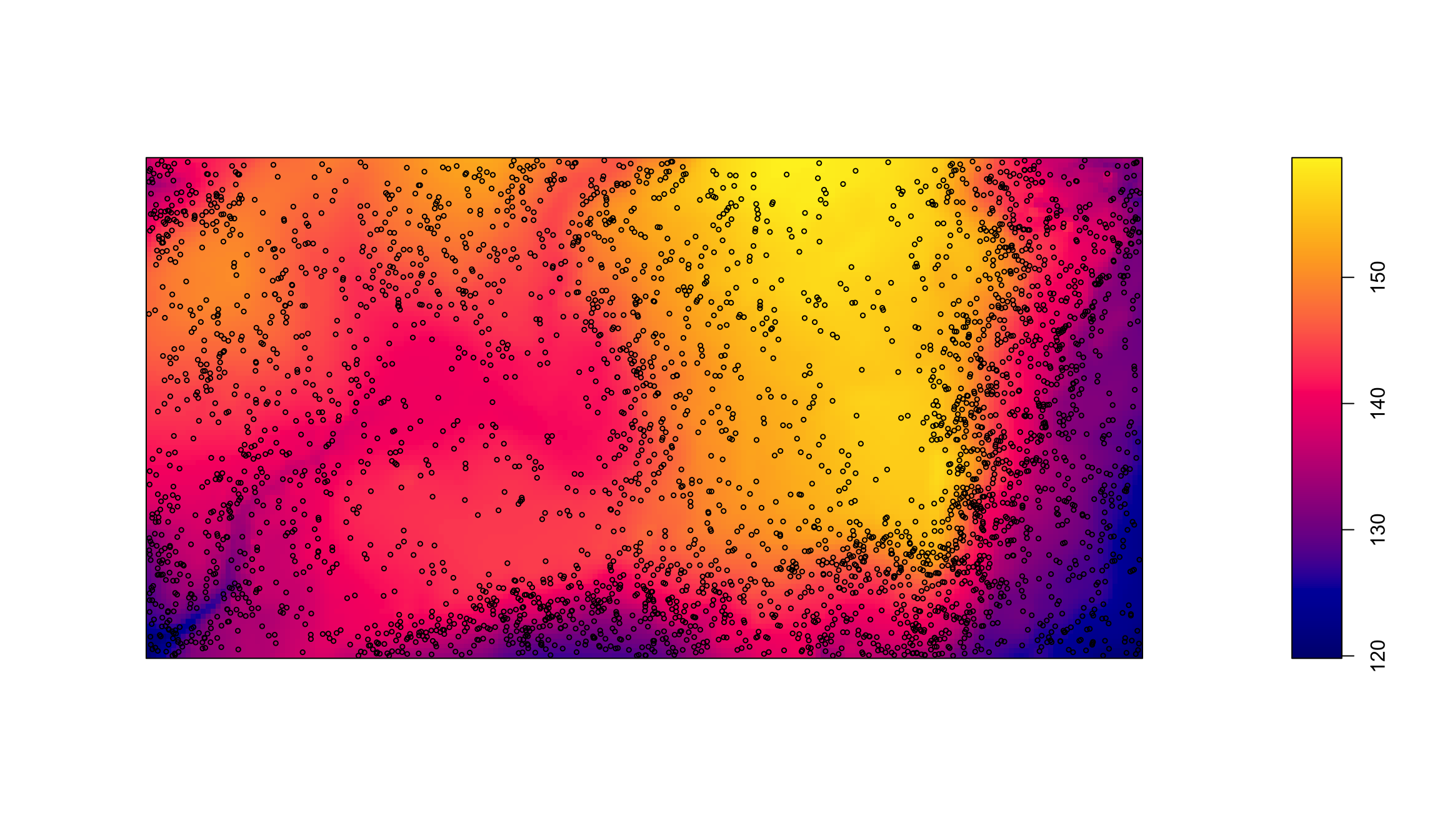
Моделирование
Методом Льюиса-Шедлера можно смоделировать альтернативные конфигурации неоднородного процесса:
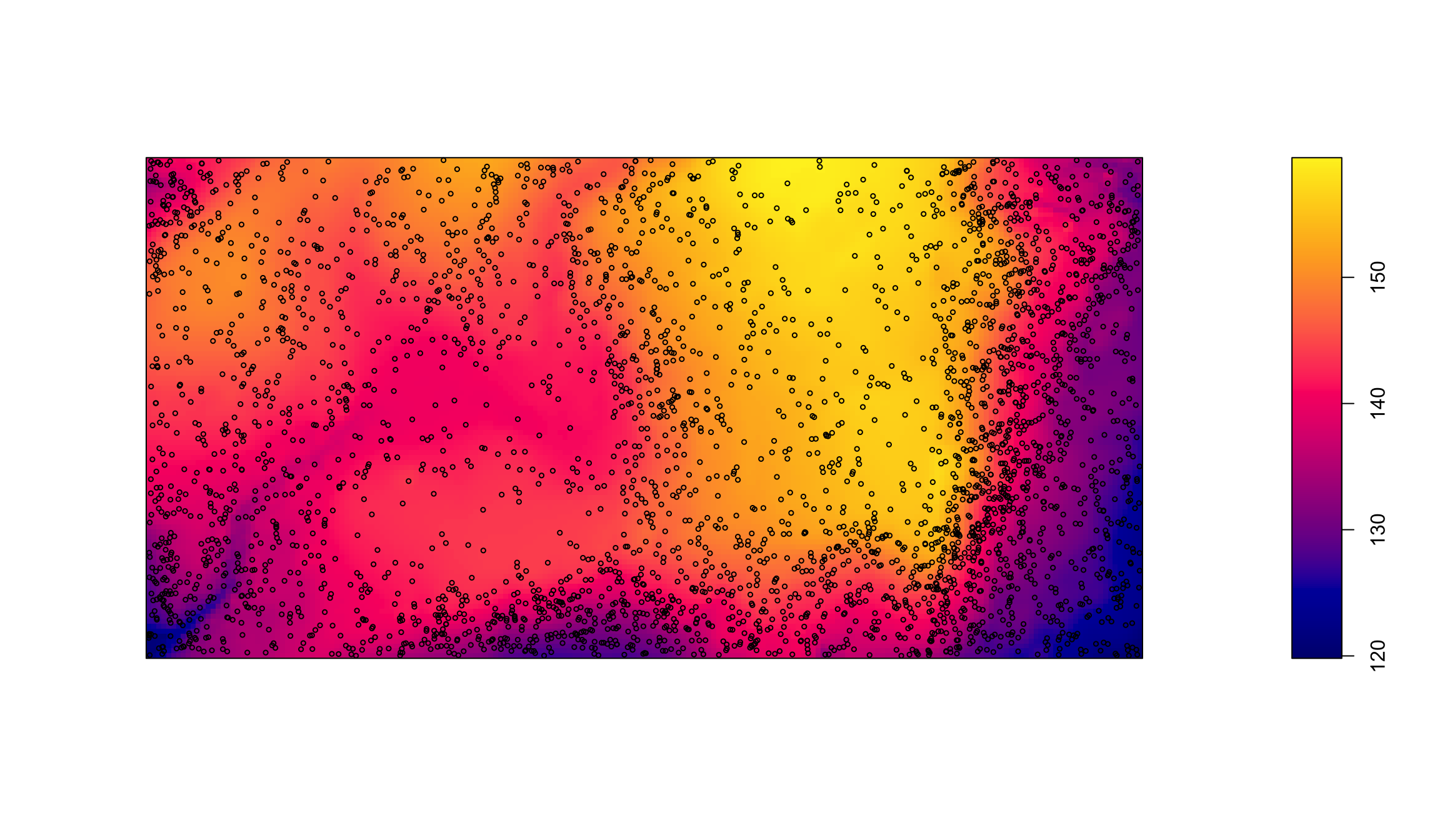
Направления использования
Некоторые примеры географических явлений и систем, для анализа которых будет полезен инструментарий точечных процессов:
- Размещение населенных пунктов и объектов сферы услуг.
- Местоположение средств передвижения (авто, самокат) и абонентов сотовой сети.
- Особенности пространственного распределения представителей растительного и животного мира (норы, гнезда и т.д.)
- Плотность распределения форм рельефа и термокарстовых озер, их упорядоченность на местности.
- Месторождения и их связь с геологическими линеаментами.
- Точечный трекинг циклонов и дрейфующих буев.
Словарик
Случайный процесс
Точечный процесс
Точечный паттерн
Пуассоновский процесс
Неоднородный процесс
Кластерный процесс
Регулярный процесс
Плотность простр. распред.
Ядерное сглаживание
Эмпирическая функция распределения
Random process
Point process
Point pattern
Poisson process
Inhomogeneous process
Cluster process
Regular process
Spatial density
Kernel smoothing
Cumulative distribution function
Библиография
Самсонов Т. Е. Основы геоинформатики: курс лекций