Модель OGC Simple Features

Геоинформатика I. Базы пространственных данных

Самсонов Тимофей Евгеньевич

13 мая 2024 г.

Simple Features

Simple Features — стандарт OGC (2010), который определяет общую модель хранения и доступа к простым (векторным) объектам.

все геометрии состоят из точек;
все точки в геометрии имеют одинаковую размерность;
размерность точек может быть 2, 3 или 4.

В дополнение к обязательным измерениям \(X\) и \(Y\) возможны:

\(Z\), обозначающее высоту
\(M\), обозначающее некоторую меру — например, время

Существует 4 варианта координат: \(XY\), \(XYZ\), \(XYM\) и \(XYZM\).

В географических координатах \(X\) — долгота, \(Y\) — широта.

Иерархия классов

Модель Simple Features представляет собой иерархию классов, между которыми существуют отношения наследования (△) и коллекции (♢).

Geometry

Все объекты типа Simple Features наследуют свойства от базового класса GEOMETRY. Механизм этого наследования основан на следующих принципах:

GEOMETRY представляет собой абстрактный класс, т.е. вы не можете создать экземпляр этого класса.
Все подклассы геометрий являются замыканиями, т.е. включают границу в множество точек.
На уровне класса GEOMETRY определен интерфейс — набор методов, которые позволяют получить информацию об объекте.
Реализация интерфейса зависит от конкретного класса.
С каждым классом геометрии ассоциированы системы отсчета, которые определяют пространственные (\(XYZ\)) и дополнительные (\(M\)) измерения.

Интерфейс класса `GEOMETRY`

Метод	Описание
`Dimension()`	Пространственная размерность данного геометрического объекта. Меньше или равна размерности координат. Для гетерогенных коллекций — максимальная размерность содержимых объектов.
`GeometryType()`	Имя подтипа класса `GEOMETRY`, экземпляром которого является данный объект.
`SRID()`	Идентификатор пространственной системы отсчета (SRS) данного объекта. Как правило, является внешним ключом к таблице систем отсчета.

Интерфейс класса `GEOMETRY`

Метод	Описание
`Envelope()`	Минимальный ограничивающий прямоугольник данного объекта, параллельный осям координат. Полигон, определяемый углами \((X_{min}, Y_{min})\), \((X_{min}, Y_{max})\), \((X_{max}, Y_{max})\), \((X_{max}, Y_{min})\), \((X_{min}, Y_{min})\). При этом в фактических реализациях достаточно указать минимумы и максимумы.
`AsText()`	Экспортирует данный геометрический объект в конкретное представление вида Well-Known Text (WKB)
`AsBinary()`	Экспортирует данный геометрический объект в конкретное представление вида Well-Known Binary (WKB)

Интерфейс класса `GEOMETRY`

Метод	Описание
`IsEmpty()`	Возвращает `TRUE` (\(1\)), если данный геометрический объект пуст, т.е. представляет пустое множество точек \(\varnothing\) в координатном пространстве; возвращает `FALSE` (\(0\)) в противном случае.
`IsSimple()`	Возвращает `TRUE` (\(1\)), если данный геометрический объект не содержит аномальных точек, таких как самопересечения и самокасания; возвращает `FALSE` (\(0\)) в противном случае.

Интерфейс класса `GEOMETRY`

Метод	Описание
`Is3D()`	Возвращает `TRUE` (\(1\)), если данный объект имеет координаты \(Z\).
`IsMeasured()`	Возвращает `TRUE` (\(1\)), если данный объект имеет координаты \(M\).
`Boundary()`	Возвращает замыкание комбинаторной границы данного объекта

Важно

Названия методов в программных реализациях Simple Features могут отличаться от предлагаемых в стандарте. Однако наличие соответствующих методов является условием реализации стандарта.

Граница и замыкание

Граничная точка: Точка, в любой окрестности которой находятся как принадлежащие, так и не принадлежащие множеству точки
Граница множества \(\partial A\): Совокупность граничных точек множества
Замыкание множества \(\overline A\): Объединение множества и его границы: \(\overline A = A \cup \partial A\)
Дополнение множества \(A^-\), вложенного в \(\mathbb R^n\) (\(A \subset \mathbb R^n\)): Множество всех точек \(\mathbb R^n\), не являющихся элементами множества: \(A^- = \mathbb R^n \backslash A\)
Внутренность множества (\(A^{\circ}\)): Объединение всех открытых подмножеств множества: \(A^\circ = \mathbb R^n \backslash \overline{A^-}\)

Топологическая граница

Симплекс

Симплекс \(\Delta^n\): Геометрическая фигура, являющаяся \(n\)-мерным обобщением треугольника
Остов симплекса: Множество его вершин
Грань симплекса размерности \(s\): \(s\)-мерный симплекс, остов которого является подмножеством остова \(\Delta^n\).
Ребро — это грань размерности \(1\).

Комплекс

Симплициальный комплекс \(\mathcal K\)

Множество симплексов, удовлетворяющее условиям:

Все грани каждого симплекса из \(\mathcal K\) также принадлежат \(\mathcal K\)
Непустое пересечение двух симплексов \(\sigma_1, \sigma_2 \in \mathcal K\) является гранью как \(\sigma_1\), так и \(\sigma_2\).

Симплициальный \(n\)-комплекс \(\mathcal K\)

\(\mathcal K\), в котором наибольшее измерение какого-либо симлекса равно \(n\)

Триангуляция

Разбиение геометрического объекта на симплексы

Комбинаторная граница

Комбинаторная граница \(\partial \mathcal K\) \(n\)-комплекса \(\mathcal K\): Множество \((n-1)\)-симплексов \(\mathcal K\), каждый из которых входит в состав только одного \(n\)-симплекса \(\mathcal K\).

Граница Simple Features

Замыкание комбинаторной границы данного объекта

Геометрическая коллекция

GEOMETRYCOLLECTION — коллекция геометрических элементов

Единственное ограничение: все элементы коллекции должны иметь единую пространственную систему отсчета.
Подклассы могут накладывать дополнительные ограничения.
Порядок элементов коллекции не имеет значения.
Интерфейс должен поддерживать методы NumGeometries() и GeometryN()

Метод	Назначение
`NumGeometries()`	Возвращает количество геометрий в данной геометрической коллекции
`GeometryN(n)`	Возвращает \(n\)-ную геометрию в данной геометрической коллекции

Точка (`POINT`)

POINT — \(0\)-мерный геометрический объект, единичное местоположение

Граница POINT — пустое множество: \(\partial A = \varnothing\)

Интерфейс точки должен поддерживать возвращение ее координат:

Метод	Назначение
`X()`	Координата \(x\) данного объекта `POINT`
`Y()`	Координата \(y\) данного объекта `POINT`
`Z()`	Координата \(z\) данного объекта `POINT`, или `NULL` если не задано.
`M()`	Координата \(m\) данного объекта `POINT`, или `NULL` если не задано.

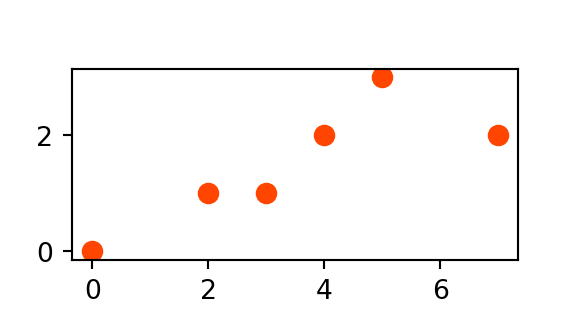
Мультиточка (`MULTIPOINT`)

MULTIPOINT — \(0\)-мерная геометрическая коллекция объектов класса POINT.

Элементы коллекции не связаны и не имеют какого-либо смыслового упорядочения (наследуется свойство GEOMETRYCOLLECTION ).
Граница MULTIPOINT — пустое множество: \(\partial A = \varnothing\).
Объект MULTIPOINT является простым, если ни одна пара POINT в его коллекции не совпадает.

flowchart LR
  A(MULTIPOINT) -->|"GeometryN( 0 )"| B(POINT)
  B -->|"X( )"| C(X)
  B -->|"Y( )"| D(Y)

Кривая (`CURVE`)

CURVE — одномерный геометрический объект, хранимый в виде последовательности точек.

Кривая определяется как непрерывное отображение отрезка в пространство:

\[f: [a, b] \rightarrow R^n\]

Это абстрактный класс, вы не можете создать объект CURVE.
Интерполяция между точками определяется конкретным подклассом CURVE.
Стандарт определяет только подкласс LINESTRING, в котором используется линейная интерполяция.

Кривая (`CURVE`)

Кривая является простой, если она не проходит дважды через одну и ту же точку, за исключением начальной и конечной точки:

\[ \texttt{f.IsSimple()} \Leftrightarrow \boxed{f(t_1)=f(t_2) \land t_1 \neq t_2 \color{red}{\Rightarrow} t_1 = a \land t_2 = b} \]

Кривая является замкнутой, если ее начальная точка равна конечной точке:

\[ \texttt{f.IsClosed()} \Leftrightarrow \boxed{f(a)=f(b)} \]
Граница замкнутой кривой является пустым множеством:

\[ \texttt{f.IsClosed()} \Leftrightarrow \boxed{\partial f=\varnothing} \]

Кривая (`CURVE`)

Граница незамкнутой кривой содержит ее конечные точки:

\[ \texttt{!f.IsClosed()} \Leftrightarrow \boxed{\partial f=\{f(a), f(b)\}} \]
Простая и замкнутая кривая является кольцом (RING).
Интерфейс объекта CURVE включает следующие методы:

Метод	Назначение
`Length()`	Длина данного объекта `CURVE` в ассоциированной СК
`StartPoint()`	Начальная точка данного объекта `CURVE`
`EndPoint()`	Конечная точка данного объекта `CURVE`
`IsClosed()`	`TRUE`, если `StartPoint() == EndPoint()`
`IsRing()`	`TRUE`, если `IsSimple()` и `StartPoint() == EndPoint()`

Линия (`LINESTRING`, `LINE`, `LINEARRING`)

LINESTRING — это CURVE с линейной интерполяцией между точками.

Каждая пара последовательных точек определяет отрезок
LINE — это LINESTRING из двух точек
LINEARRING — это простой замкнутый LINESTRING
Интерфейс содержит дополнительные методы:

Метод	Назначение
`NumPoints()`	Количество точек в данном объекте `LINESTRING`
`PointN(n)`	\(n\)-я точка данного объекта `LINESTRING`

Мультикривая (`MULTICURVE`)

MULTICURVE представляет 1-мерный подкласс GEOMETRYCOLLECTION — коллекцию объектов CURVE.

MULTICURVE как и CURVE является абстрактным классом. Вы не можете создать объект данного класса.
MULTICURVE является простым, если каждый его элемент является простым, а их пересечения происходят только в граничных точках.
Точка принадлежит границе объекта MULTICURVE если она принадлежит границам нечетного числа его элементов.
Объект MULTICURVE замкнут, если замкнуты всего его элементы.
Граница замкнутого объекта MULTICURVE всегда пуста.

Мультикривая (`MULTICURVE`)

MULTICURVE представляет 1-мерный подкласс GEOMETRYCOLLECTION — коллекцию объектов CURVE.

Интерфейс MULTICURVE дополнительно к GEOMETRYCOLLECTION реализует следующие методы:

Метод	Назначение
`IsClosed()`	`TRUE` (\(1\)) если данный объект `MULTICURVE` является замкнутым (т.е. каждый объект `CURVE` в коллекции является замкнутым. Возвращает `FALSE` (\(0\)) в противном случае
`Length()`	Длина данного объекта `MULTICURVE`, которая равна сумме длин элементов коллекции.

Мультилиния (`MULTILINESTRING`)

MULTILINESTRING — это MULTICURVE с элементами класса LINESTRING.

Поверхность (`SURFACE`)

SURFACE — это \(2\)-мерный геометрический объект.

Простая поверхность состоит из единичной области (“patch”), которая соответствует одной внешней границе, а также \(0\) и более внутренних границ.
Простая поверхность в 3-мерном пространстве изоморфна планарной поверхности с точностью до поворота на плоскость \(z = 0\).
Полиэдральная поверхность формируется “склеиванием” простых поверхностей по общим границам (полиэдр — объединение многогранников).
Если нормали всех компонент полиэдральной поверхности параллельны, то она может быть представлена в виде простой поверхности.

Поверхность (`SURFACE`)

SURFACE — это абстрактный класс, вы не можете создать объект этого класса.
Граница объекта SURFACE — это множество объектов класса CURVE, соответствующих его внешней и (опционально) внутренним границам.
Интерфейс класса имеет дополнительные методы:

Метод	Назначение
`Area()`	Площадь данного объекта `SURFACE` в его системе координат
`Centroid()`	Математический центроид данного объекта `SURFACE` как объект класса `POINT`. Может находиться за пределами объекта.
`PointOnSurface()`	Объект класса `POINT`, который гарантированно принадлежит данному объекту `SURFACE`.

Полигон (`POLYGON`) и треугольник (`TRIANGLE`)

POLYGON — плоская поверхность с одной внешней и 0+ внутренних границ

Границы POLYGON имеют класс LINEARRING.
Внешняя граница против часовой стрелки, внутренние — по часовой.
TRIANGLE — это POLYGON из 3 различных, неколлинеарных точек.

Метод	Назначение
`ExtriorRing()`	Внешнее кольцо данного `POLYGON` в виде `LINESTRING`
`NumInteriorRing()`	Количество внутренних колец данного `POLYGON`
`InteriorRingN(n)`	\(n\)-ное внутреннее кольцо данного `POLYGON` в виде `LINESTRING`

Полигон (`POLYGON`)

Дополнительные проверки:

Внутренняя область полигона \(P^\circ\) — линейно связное множество.
Внешняя область полигона \(P^-\) с 1 и более дырок — линейно несвязное множество.
Границы полигона не могут перекрываться, а их пересечение возможно только в форме касания в точке.
Полигон не может иметь линий разреза, шипов и проколов. Формально это означает, что полигон совпадает с замыканием его внутренней области: \(P = \overline{P^\circ}\).

`POLYHEDRALSURFACE` и `TIN`

POLYHEDRALSURFACE — коллекция полигонов, которые имеют общие границы.

Для каждой пары касающихся полигонов их общая граница должна быть представима в виде коллекции объектов LINESTRING.
Каждый такой LINESTRING должен входить в состав не более чем \(2\)-х полигонов.
Направление обхода контура у всех граней POLYHEDRALSURFACE должно быть одинаковым. Два соседних полигона проходят общую границу в противоположных направлениях.
TIN (Triangular Irregular Network) — это POLYHEDRALSURFACE, который состоит из объектов класса TRIANGLE.

`POLYHEDRALSURFACE` и `TIN`

Интерфейс POLYHEDRALSURFACE дополнительно поддерживает следующие методы:

Метод	Назначение
`NumPatches()`	Количество полигонов данного объекта `POLYHEDRALSURFACE`
`PatchN(n)`	\(n\)-ный полигон данного объекта `POLYHEDRALSURFACE` в виде объекта `POLYGON`
`BoundingPolygons(p)`	Коллекция полигонов, которые граничат с `p` в данном объекте `POLYHEDRALSURFACE` в виде объекта `MULTIPOLYGON`.
`IsClosed()`	`TRUE`, если поверхность замкнута сама на себя, т.е. не имеет границы и оконтуривает сплошное тело.

Мультиповерхность (`MULTISURFACE`)

MULTISURFACE — 2-мерный объект класса GEOMETRYCOLLECTION, элементами которого являются объекты класса SURFACE.

Внутренние области любых двух поверхностей в коллекции не могут пересекаться.
Границы любых двух поверхностей в коллекции могут пересекаться только в конечном числе точек.
В случае касания вдоль кривой поверхности могут быть объединены.
Дополнительные методы аналогичны методам SURFACE.

Мультиполигон (`MULTIPOLYGON`)

MULTIPOLYGON — это объект класса MULTISURFACE, элементы которого являются объектами класса POLYGON.

MULTIPOLYGON наследует все ограничения, действующие для объектов классов MULTISURFACE и POLYGON.
Внутренняя область объекта MULTIPOLYGON , включающего 2 и более полигонов, не является линейно связной. Количество компонент = количество полигонов.
Границей объекта MULTIPOLYGON является множество замкнутых объектов LINESTRING, соответствующих границам вложенных объектов POLYGON.
POLYHEDRALSURFACE не является мультиполигоном, т.к. может нарушать правило касания в конечном числе точек.

Иерархия классов

Библиография

OGC. 2010. «OpenGIS® Implementation Standard for Geographic information - Simple feature access - Part 1: Common architecture». Open Geospatial Consortium. https://www.ogc.org/standards/sfa.

Модель OGC Simple Features

Simple Features

Иерархия классов

Geometry

Интерфейс класса GEOMETRY

Интерфейс класса GEOMETRY

Интерфейс класса GEOMETRY

Интерфейс класса GEOMETRY

Граница и замыкание

Топологическая граница

Симплекс

Комплекс

Комбинаторная граница

Граница Simple Features

Геометрическая коллекция

Точка (POINT)

Мультиточка (MULTIPOINT)

Кривая (CURVE)

Кривая (CURVE)

Кривая (CURVE)

Линия (LINESTRING, LINE, LINEARRING)

Мультикривая (MULTICURVE)

Мультикривая (MULTICURVE)

Мультилиния (MULTILINESTRING)

Поверхность (SURFACE)

Поверхность (SURFACE)

Полигон (POLYGON) и треугольник (TRIANGLE)

Полигон (POLYGON)

POLYHEDRALSURFACE и TIN

POLYHEDRALSURFACE и TIN

Мультиповерхность (MULTISURFACE)

Мультиполигон (MULTIPOLYGON)

Иерархия классов

Библиография

Интерфейс класса `GEOMETRY`

Интерфейс класса `GEOMETRY`

Интерфейс класса `GEOMETRY`

Интерфейс класса `GEOMETRY`

Точка (`POINT`)

Мультиточка (`MULTIPOINT`)

Кривая (`CURVE`)

Кривая (`CURVE`)

Кривая (`CURVE`)

Линия (`LINESTRING`, `LINE`, `LINEARRING`)

Мультикривая (`MULTICURVE`)

Мультикривая (`MULTICURVE`)

Мультилиния (`MULTILINESTRING`)

Поверхность (`SURFACE`)

Поверхность (`SURFACE`)

Полигон (`POLYGON`) и треугольник (`TRIANGLE`)

Полигон (`POLYGON`)

`POLYHEDRALSURFACE` и `TIN`

`POLYHEDRALSURFACE` и `TIN`

Мультиповерхность (`MULTISURFACE`)

Мультиполигон (`MULTIPOLYGON`)