Глава 3 Географически взвешенная регрессия
3.1 Краткий обзор
Для просмотра презентации щелкните на ней один раз левой кнопкой мыши и листайте, используя кнопки на клавиатуре:
Презентацию можно открыть в отдельном окне или вкладке браузере. Для этого щелкните по ней правой кнопкой мыши и выберите соответствующую команду.
3.2 Географически взвешенная регрессия (GWR)
В стандартной модели линейной регрессии параметры модели предполагаются постоянными:
\[\mathbf{y} = \mathbf{X} \boldsymbol\beta + \boldsymbol\epsilon,\]
Для \(i\)-й локации решению выглядит следующим образом:
\[y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_m x_{mi} + \epsilon_i\]
Коэффициенты находятся методом наименьших квадратов:
\[\mathbf{\beta}' = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{Y}\]
Такой подход, однако не учитывает того, что характер зависимости между переменными может меняться по пространству.
В географически взвешенной регрессионной модели веса определяются для каждой локации:
\[y_i = \beta_{0i} + \beta_{1i} x_{1i} + \beta_{2i} x_{2i} + ... + \beta_{mi} x_{mi} + \epsilon_i\]
В этом случае область оценки параметров \(\mathbf{\beta}\) ограничивается некой окрестностью точки \(i\). Математически это достигается применением весовых коэффициентов для данных независимых переменных:
\[\mathbf{\beta}'(i) = (\mathbf{X}^T \color{blue}{\mathbf{W}(i)}\mathbf{X})^{-1} \mathbf{X}^T \color{blue}{\mathbf{W}(i)} \mathbf{Y},\]
где \(\mathbf{W}(i)\) есть матрица весов для точки \(i\). Коэффициенты матрицы подбираются таким образом, что близкие локации получают более высокий вес.
Матрица \(\mathbf{W}(i)\) имеет размер \(n \times n\), где \(n\) — число точек наблюдений:
\[\mathbf{W}(i) = \begin{bmatrix} w_{i1} & 0 & 0 & \dots & 0 \\ 0 & w_{i2} & 0 & \dots & 0 \\ 0 & 0 & w_{i3} & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & w_{in} \end{bmatrix},\]
где \(w_{ik}\) есть вес, который имеет точка \(k\) при локальной оценке параметров в точке \(i\).
3.2.1 Весовые функции
Весовая функция должна быть убывающей. Существует множество вариантов таких функций, но наиболее часто используются гауссоподобные варианты:
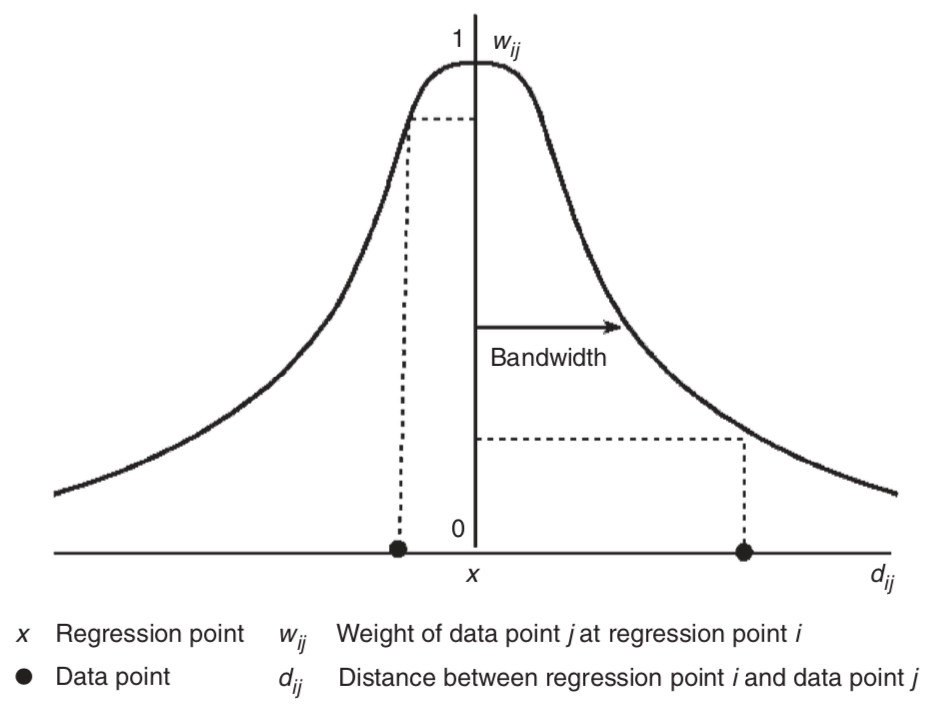
Рис. 2.2: Весовая функция
В случае фиксированной весовой функции окрестность всегда имеет фиксированный размер:
\[w_{ij} = \operatorname{exp}\{-\frac{1}{2} (d_{ij}/h)^2\},\]
где \(d_{ij}\) есть расстояние, \(h\) — полоса пропускания.
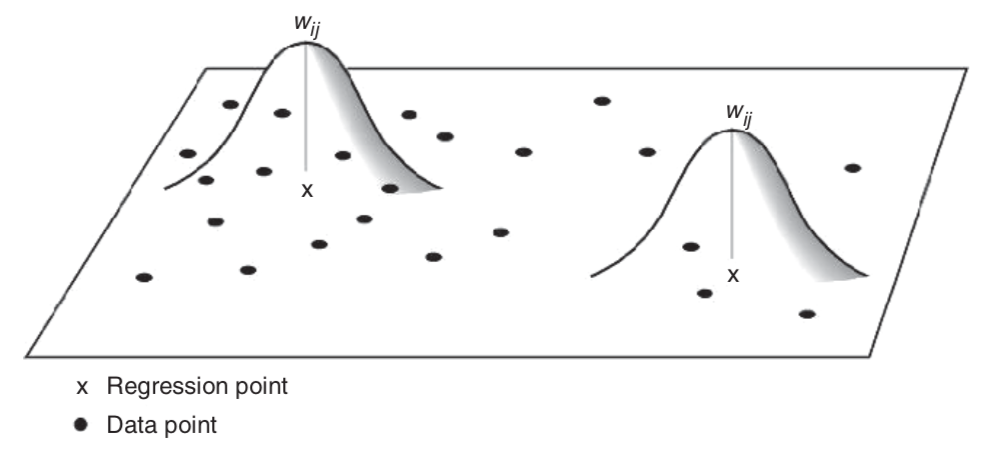
Рис. 2.3: Фиксированная весовая функция
В случае адаптивной весовой функции окрестность ограничивается \(N\) ближайшими точками. За пределами этой окрестности веса принимаются равными нулю:
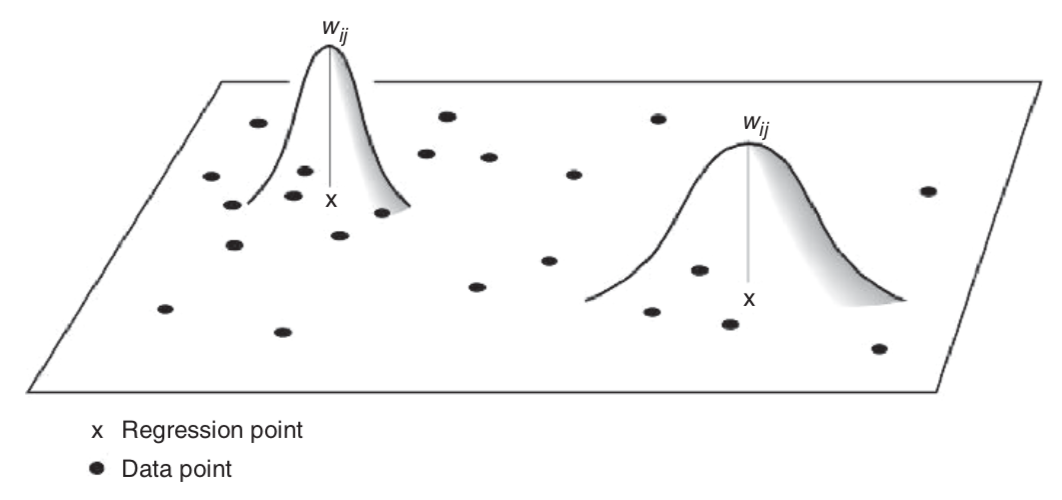
Рис. 2.4: Адаптивная весовая функция
Полоса пропускания \(h\) обладает следующими особенностями:
- малая полоса пропускания приводит к большой дисперсии локальных оценок;
- большая полоса пропускания приводит к смещенности оценки;
- при \(h \rightarrow \infty\) локальная модель приближается к глобальной регрессии;
- при \(h \rightarrow 0\) локальная модель «сворачивается» вокруг данных.
3.2.2 Практический анализ
В качестве примера проанализируем каким образом цена жилья зависит от количества комнат на примере данных по стоимости недвижимости в Бостоне, доступных на данном сайте, и выгруженных с североамериканского информационного портала недвижимости padmapper.com:
realest = read_delim(url('https://www.jefftk.com/apartment_prices/apts-1542637382.txt'),
delim = ' ',
col_names = c('price', 'rooms', 'id', 'lon', 'lat')) %>%
st_as_sf(coords = c('lon', 'lat'), crs = 4326) %>%
st_transform(3395)
# tmap_mode('view')
tm_shape(realest) +
tm_bubbles(col = 'price',
size = 'rooms',
style = 'fixed',
breaks = c(0, 1000, 2000, 3000, 4000, 5000, 10000, max(realest$price)),
scale = 0.25,
palette = colorRampPalette(c('steelblue4', 'orange', 'darkred'))(7),
alpha = 0.8) +
tm_view(symbol.size.fixed = TRUE)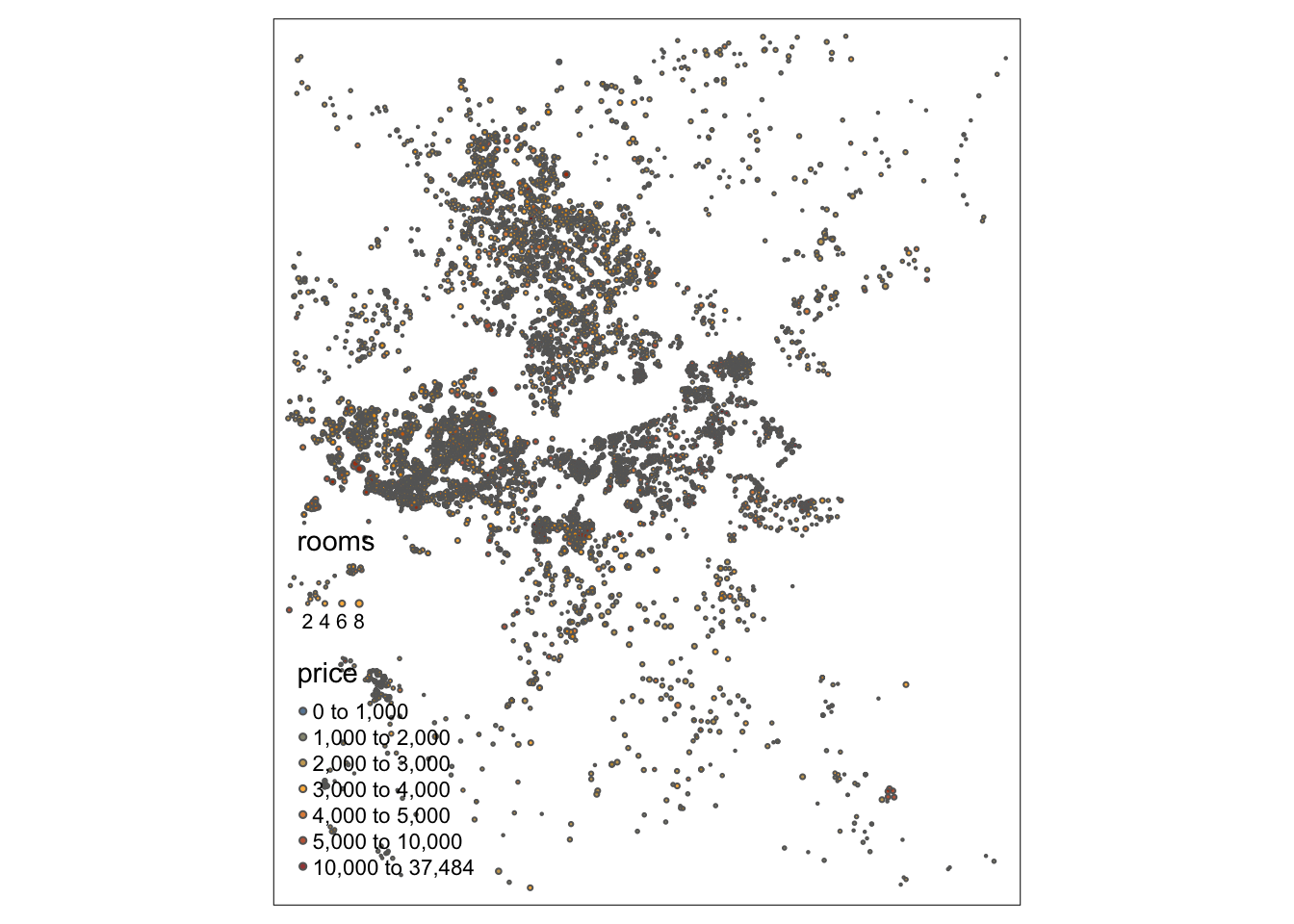
Для того чтобы оценить пространственую неравномерность реакции стоимости жилья на увеличение количества комнат, построим модель географически взвешенной регрессии:
samples = realest %>% dplyr::sample_n(1000) %>% as('Spatial')
(gwr_res = gwr.basic(price ~ rooms, data = samples, bw = 1000, kernel = 'gaussian'))
tm_shape(gwr_res$SDF) +
tm_bubbles(col = 'rooms', # это не количество комнат, а коэффициент регрессии
style = 'quantile',
scale = 0.3,
palette = 'Reds',
alpha = 0.5) +
tm_view(symbol.size.fixed = TRUE)Как видно, модель GWR наглядно показывает наличие пространственной гетерогенности (неоднороности) в распределении показателя. Четко видны районы (в основном цеентральные, но также и часть окраинных), где стоимость жилья резко возрастает при увеличении количества комнат.