8  Временные ряды

8.1 Предварительные требования

Для работы по теме текущей лекции вам понадобятся пакеты из tidyverse. Для работы с временными данными мы воспользуемся пакетом lubridate, который входит в tidyverse, но автоматически не подключается в сессию. Мы также воспользуемся пакетом gganimate, который позволяет анимировать графики, построенные с помощью ggplot, и пакетами tsibble, feasts и fable для анализа временных рядов.

8.2 Создание и преобразование дат и времени

Напомним, что текущее время и дату можно получить с помощью системных функций Sys.Date() и Sys.time():

(date = Sys.Date())
[1] "2023-12-19"
(time = Sys.time())
[1] "2023-12-19 09:31:33 MSK"

Полученные объекты имеют типы Date и POSIXct:

class(date)
[1] "Date"
class(time)
[1] "POSIXct" "POSIXt"

Несмотря на то, что время и даты печатаются на экран в виде человекочитаемых строк, их внутреннее представление выражается в количестве дней (для дат) и секунд (для времени в форммате POSIXct) начиная с некоторой точки отсчета. Такой точкой отсчета по умолчанию является начало эпохи UNIX, соответстующее \(1\) января \(1970\) года по гринвичскому (UTC) времени. Чтобы убедиться в этом, воспользуемся функцией difftime, доступной в базовом R:

as.integer(date)
[1] 19710
difftime(date, as.Date('1970-01-01'))
Time difference of 19710 days
as.integer(time)
[1] 1702967493
difftime(time, as.POSIXct('1970-01-01 00:00:00', tz = 'UTC'), units = 'secs')
Time difference of 1702967494 secs

Работа с датами и временем может быть достаточно утомительной при отсутствии специализированных средств. Пакет lubridate значительно облегчает эту работу. Основные функции lubridate включают синтаксический разбор (“парсинг”) дат в разных форматах, извлечение разных компонент даты и времени (секунд, минут, часов, суток, недель, годов), вычисление разностей и периодов, а также множество вспомогательных функций (хелперов), облегачающих преобразование временных данных.

Рассмотрим базовые возможности пакета на нескольких примерах.

Создание дат возможно на основе целочисленных и строковых значений:

ymd(20150515)
[1] "2015-05-15"
dmy('15052015')
[1] "2015-05-15"

Для создания отметки времени необходимо сформировать строку, которая можети быть интерпретирована должным образом. При необходимости указывается часовой пояс:

ymd_hms('2015-05-15 22:15:34') # по умолчанию Гринвичское время
[1] "2015-05-15 22:15:34 UTC"
ymd_hms('2015-05-15 22:15:34', tz = "Europe/Moscow")
[1] "2015-05-15 22:15:34 MSK"

Извлечение компоненты даты/времени — одна из самых удобных и востребованных функций lubridate. С помощью этих функций вы можете вытащить из объекта год, месяц, неделю, день, час и секунду:

year(time)
[1] 2023
month(time)
[1] 12
week(time)
[1] 51
day(time)
[1] 19
hour(time)
[1] 9
second(time)
[1] 33.91441

Обратите внимание на то, что недели отсчитываются от начала года, а не месяца.

Отдельно следует отметить функцию yday(), которая позволяет определить номер дня в году:

yday(date)
[1] 353

Замена компонент даты/времени осуществляется с использованием тех же функций. Например, если мы хотим то же число и время, но за другой (заранее известный) год и месяц, мы можем заменить соответствующие компоненты, используя оператор <-:

year(time) <- 2015
month(time) <- 01
time
[1] "2015-01-19 09:31:33 MSK"

Округление дат и времени выполняется с помощью функций round_date(), floor_date() и ceiling_date() соответственно. Например, получить первый день в текущем году можно так:

floor_date(Sys.Date(), unit = 'year')
[1] "2023-01-01"

Периоды (periods) — это промежутки дат, выраженные в годах, месяцах или днях. Их удобно использовать для того чтобы сместить текущую дату на заданный интервал. Например, к ранее определенной дате можно прибавить 1 год, 4 месяца, 3 недели и 2 дня:

date
[1] "2023-12-19"
date + years(1) + months(4) + weeks(3) + days(2)
[1] "2025-05-12"

Длительности (durations) — это промежутки времени, выраженные в секундах. Работают они в целом аналогично периодам:

dweeks(1)
[1] "604800s (~1 weeks)"
time
[1] "2015-01-19 09:31:33 MSK"
time + dweeks(1)
[1] "2015-01-26 09:31:33 MSK"
time + weeks(1)
[1] "2015-01-26 09:31:33 MSK"

Интервалы — это отрезки между двумя датами. Интервал можно преобразовывать в периоды и длительности:

(int = lubridate::interval(Sys.time(), time))
[1] 2023-12-19 09:31:34 MSK--2015-01-19 09:31:33 MSK
as.period(int, 'days')
[1] "-3256d 0H 0M -0.272432088851929S"
as.duration(int)
[1] "-281318400.272432s (~-8.91 years)"

8.3 Создание временного фрейма данных

Данные во временных рядах часто соответствуют равноотстоящим по времени срезам (раз в несколько часов, раз в день, раз в три месяца и т.д.), что обусловлено регулярным характером сбора информации (наблюдения, предоставление отчетности и т.д.). Соответствующее предположение лежит и в основе многих функций временного анализа (таких как автокорреляционная функция). Если в данных отсутствуют некоторые временные срезы, это нарушает регулярность временного ряда, что может привести к его некорректной интерпретации. Необходимо восстановить пропущенные сроки, явным образом указав, что данных на эти сроки нет.

Помимо этого, дата может быть записана в некорректной форме. Например, оператор ввода данных перепутал месяц и день 18 марта, что привело к созданию несуществующей даты 03.18 в одной из строк.

Подобные несовершенства временных рядов важно выявить на самых ранних стадиях анализа данных. Рассмотрим, как эту задачу можно решить средствами R. В качестве источника данных будем использовать данные1 об уровне воды на гидропосте Паялка (р. Умба, Мурманская область) с 1932 по 2014 год. Отсутствие информации в файле данных закодировано числом 9999:

(src = read_delim('data/in_Umba.txt', delim = ' ', 
                 col_names = c('day', 'month', 'year', 'level'), na = '9999'))
# A tibble: 30,316 × 4
     day month  year level
   <dbl> <dbl> <dbl> <dbl>
 1     1     1  1932  49.4
 2     2     1  1932  NA  
 3     3     1  1932  NA  
 4     4     1  1932  NA  
 5     5     1  1932  NA  
 6     6     1  1932  NA  
 7     7     1  1932  NA  
 8     8     1  1932  NA  
 9     9     1  1932  NA  
10    10     1  1932  47  
# ℹ 30,306 more rows

Сформируем даты на основе первых трёх столбцов и проверим, все ли из них корректны. Если компоненты даты некорректны, то функция ymв() вернет NA:

tab = src |>
    mutate(Date = ymd(paste(year, month, day)))

Функция сообщила, что один временной срез был преобразован некорректно. Можно проверить, какой именно:

tab |> 
  filter(is.na(Date))
# A tibble: 1 × 5
    day month  year level Date  
  <dbl> <dbl> <dbl> <dbl> <date>
1    29     2  1941  27.4 NA

Проверка показала, что преобразование в дату оказалось невозможно только для одной строки. В этой строке оператором была введена несуществующая дата — 29 февраля 1941 года. Этот год не является високосным, а значит количество дней в феврале должно равняться 28.

В таблице временного фрейма данных класса tsibble каждый элемент определяется временным индексом и ключом. Ключ обязательным не является. В нашем случае данные ключа не имют, т.к. переменная лишь одного типа — расход. Попробуем создать временную таблицу:

tsbl = as_tsibble(tab, index = Date)
Error in `validate_index()`:
! Column `Date` (index) must not contain `NA`.

Как видно, создать класс временного фрейма данных не получилось, потому что есть пропуски дат. Необходимо отбраковать пустые даты:

tsbl = tab |> 
  filter(!is.na(Date)) |> 
  as_tsibble(index = Date)
Error in `validate_tsibble()`:
! A valid tsibble must have distinct rows identified by key and index.
ℹ Please use `duplicates()` to check the duplicated rows.

Диагностическая информация говорит о том, что в таблице есть полностью идентичные строки. Можно их найти с помощью duplicates():

tab |> 
  filter(!is.na(Date)) |> 
  duplicates(index = Date)
# A tibble: 2 × 5
    day month  year level Date      
  <dbl> <dbl> <dbl> <dbl> <date>    
1    31    12  1942  25.4 1942-12-31
2    31    12  1942  42.8 1942-12-31

Что делать с подобными дубликатами дат — решать вам. Если известно, какие данные правильные, а какие ошибочные — можно убрать конкретные строки. Оставим только уникальные даты посредством dplyr::distinct():

tsbl = tab |> 
  filter(!is.na(Date)) |> 
  distinct(Date, .keep_all = T) |> 
  as_tsibble(index = Date)

tsbl
# A tsibble: 30,314 x 5 [1D]
     day month  year level Date      
   <dbl> <dbl> <dbl> <dbl> <date>    
 1     1     1  1932  49.4 1932-01-01
 2     2     1  1932  NA   1932-01-02
 3     3     1  1932  NA   1932-01-03
 4     4     1  1932  NA   1932-01-04
 5     5     1  1932  NA   1932-01-05
 6     6     1  1932  NA   1932-01-06
 7     7     1  1932  NA   1932-01-07
 8     8     1  1932  NA   1932-01-08
 9     9     1  1932  NA   1932-01-09
10    10     1  1932  47   1932-01-10
# ℹ 30,304 more rows

Объект tsibble создан. Наличие уникальных дат еще не говорит о том, что в датах нет пропусков. Чтобы это выяснить, можно использовать scan_gaps() (индивидуальные пропуски) или count_gaps() (периоды пропусков):

scan_gaps(tsbl)
# A tsibble: 2 x 1 [1D]
  Date      
  <date>    
1 1941-12-31
2 1942-01-01
count_gaps(tsbl)
# A tibble: 1 × 3
  .from      .to           .n
  <date>     <date>     <int>
1 1941-12-31 1942-01-01     2

Хорошим тоном является приведение всех подобных пропусков в явные пропущенные значения таблице. Их можно выполнить посредством fill_gaps():

tsbl = fill_gaps(tsbl)
scan_gaps(tsbl)
# A tsibble: 0 x 1 [?]
# ℹ 1 variable: Date <date>

На этом подготовку данных к обработке можно закончить и приступать к анализу и моделированию.

8.4 Интерполяция по времени

Одна из распространенных задач при работе с временными данными — это интерполяция по времени. Во-первых, интерполяция может использоваться для заполнения пропусков данных. Во-вторых, необходимость в интерполяции возникает когда неравномерно распределенные по времени данные надо перенести на регулярные сроки (скажем, через час), чтобы обеспечить их сравнимость с другими рядами данных. Заметим, что и в том и в другом случае необходимо учитывать автокорреляционные свойства временного ряда и с осторожностью подходить к интерполяции на длительных промежутках времени, поскольку такая интерполяция может не иметь под собой физических оснований.

8.4.1 Заполнение временных пропусков

Рассмотрим заполнение пропусков данных на примере загруженных в предыдущем параграфе данных по уровням воды на гидропосте Паялка. На первом этапе анализа пропусков данных целесообразно получить сводную таблицу, которая бы систематизировала все пропуски и непрерывные ряды данных. Для этого сначала выставим маркер data/gap (данные/пропуск) на против каждой строки в новом поле type, а затем пронумеруем все группы последовательно идущих друг за другом меток совпадающего типа. Для реализации последнего шага выполним следующее:

  • сформируем группы непрерывно идущих следом друг за другом меток одного типа, используя функцию rle (run-length encoding); полученный объект содержит вектор lengths, количество элементов которого равняется количеству групп, а значение каждого элемента равно количеству объектов соответствующей по порядку группы;
  • номер каждой группы (от 1 до количества групп) продублируем столько раз, сколько элементов содержится в каждой группе

После этого сгруппируем данные по номеру группы и вычислим дату начала, дату конца, продолжительность и тип каждого периода. Полученная таблица наглядно демонстрирует разбиение временного ряда на периоды наличия и отсутствия данных:

find_gaps = function(df, variable) {
  df |> 
    as_tibble() |>
    mutate(type = if_else(is.na(df[variable]), 'gap', 'data'),
           num = with(rle(type), rep(seq_along(lengths), lengths))) |> 
    group_by(num) |> 
    summarise(start_date = min(Date),
              end_date = max(Date),
              duration = end_date - start_date + 1,
              type = first(type))
}
timerep = find_gaps(tab, 'level')

Путём интерполяции можно заполнить все пропуски в данном ряду, однако достоверность (правдоподобие) интерполяции будет снижаться при увеличении длины пропуска. Критическую длину пропуска целесообразно связать с пороговым значением автокорреляции — коэффициента корреляции исходного ряда данных и его копии, полученной со сдвигом \(\tau\). Автокорреляцию как правило рассчитываеют не при фиксированном сдвиге, а для серии сдвигов. Полученная функция показывает зависимость автокорреляции от величины сдвига и носит название автокорреляционной функции (АКФ):

\[\Psi(\tau) = \int_{-\infty}^{+\infty} f(t) f^* (t - \tau) dt,\] где \(^*\) означает комплексное сопряжение (для вещественнозначных функций эту звездочку можно игнорировать, она нужна в целях обобщения понятия автокорреляции для случайных процессов, сечения которых являются комплексными случайными переменными).

Автокорреляционная функция случайного процесса \(X(t)\) будет иметь вид:

\[K(\tau) = \mathbb E \big[X(t) X^* (t - \tau) \big],\] где \(\mathbb E \big[~ \big]\) — математическое ожидание.

Для нецикличных процессов, плавно изменяющихся во времени, при увеличении \(\tau\) значение АКФ падает, а это означает, что установив минимально допустимое значение автокорреляции, можно выяснить соответствующий ему сдвиг по времени. Найденная величина и будет максимально допустимой при интерполяции длиной пропуска.

Для вычисления автокорреляционной функции можно воспользоваться встроенной функцией acf(), однако с ней может быть не очень удобно работать, поскольку оне не умеет работать с пропусками в данных, и нужно искать длительный промежуток непрерывных измерений. Вместо этого воспользуемся функцией ACF() из пакета feasts:

acorr = tsbl |> ACF(level)
acorr
# A tsibble: 41 x 2 [1D]
        lag   acf
   <cf_lag> <dbl>
 1       1D 0.994
 2       2D 0.982
 3       3D 0.964
 4       4D 0.943
 5       5D 0.919
 6       6D 0.893
 7       7D 0.866
 8       8D 0.839
 9       9D 0.812
10      10D 0.786
# ℹ 31 more rows

Визуализировать результаты можно посредством функции autoplot() из того же пакета:

autoplot(acorr)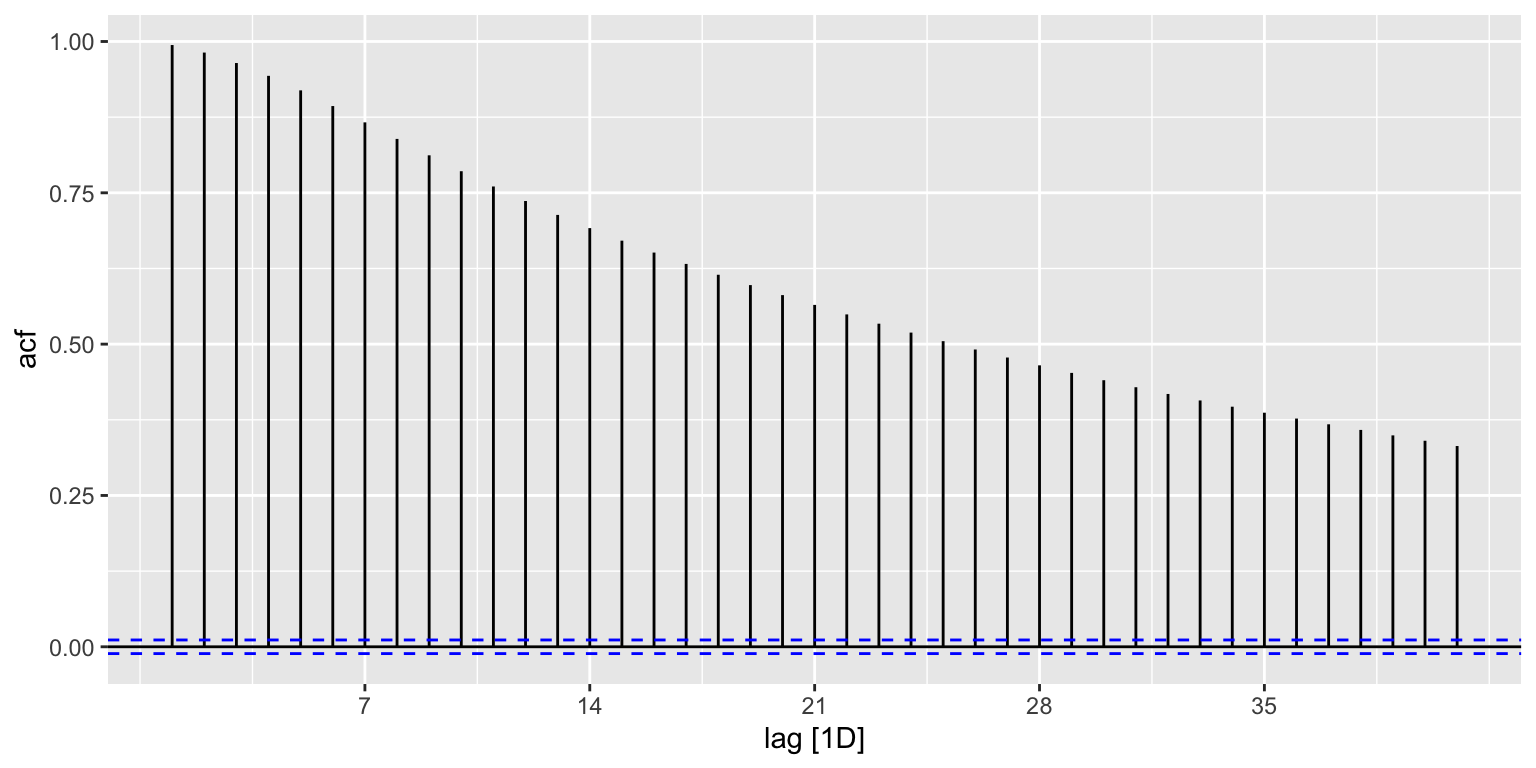

Результат соответствует нашим ожиданиям: автокорреляционная функция монотонно убывает при увеличении сдвига по времени. Осталось устновить пороговое значение автокорреляции и найти соответствующий ему сдвиг.

В гидрологии за допустимую величину автокорреляции при восстановлении рядов данных принято брать значение, равное \(0.7\). Найдем индекс первого элемента менее данной величины, используя функцию detect_index() из пакета purrr:

(max_dur = purrr::detect_index(acorr$acf, ~ .x < 0.7))
[1] 14

Полученное значение говорит нам о том, что при заданном допуске допустимо интерполировать значения в пропусках данных короче, чем 14 дней.

Интерполяцию можно проводить разными способами, но самый правильный при отсутствии связанных переменных — это авторегрессионные модели. Для начала визуализируем участок в окрестности одного из пробелов

autoplot(tsbl, level, size = 1) +
  scale_x_date(limits = c(ymd(19320101), ymd(19350101)))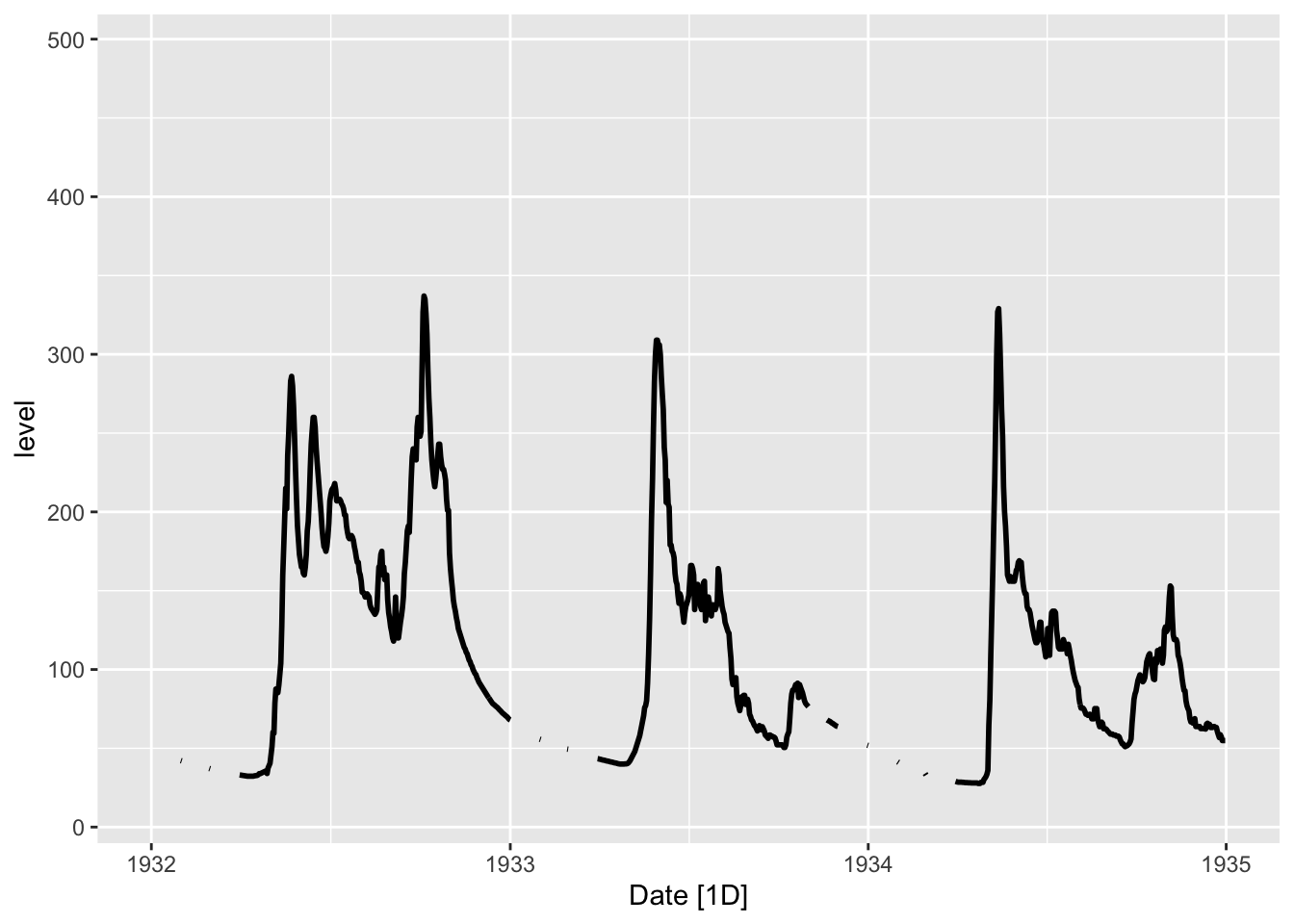

Для выполнения обычной линейной интерполяции между пропускаи воспользуемся функцией na.approx() из пакета zoo и округлим полученные значения до одного знака после запятой (что соответствует точности исходных данных):

(tsbl_int = tsbl |> 
  mutate(level_interp = zoo::na.approx(level, maxgap = max_dur) |> round(1)))
# A tsibble: 30,316 x 6 [1D]
     day month  year level Date       level_interp
   <dbl> <dbl> <dbl> <dbl> <date>            <dbl>
 1     1     1  1932  49.4 1932-01-01         49.4
 2     2     1  1932  NA   1932-01-02         49.1
 3     3     1  1932  NA   1932-01-03         48.9
 4     4     1  1932  NA   1932-01-04         48.6
 5     5     1  1932  NA   1932-01-05         48.3
 6     6     1  1932  NA   1932-01-06         48.1
 7     7     1  1932  NA   1932-01-07         47.8
 8     8     1  1932  NA   1932-01-08         47.5
 9     9     1  1932  NA   1932-01-09         47.3
10    10     1  1932  47   1932-01-10         47  
# ℹ 30,306 more rows
autoplot(tsbl_int, level_interp, color = 'red', size = 1) +
  geom_line(aes(Date, level), tsbl, size = 1) +
  scale_x_date(limits = c(ymd(19320101), ymd(19350101)))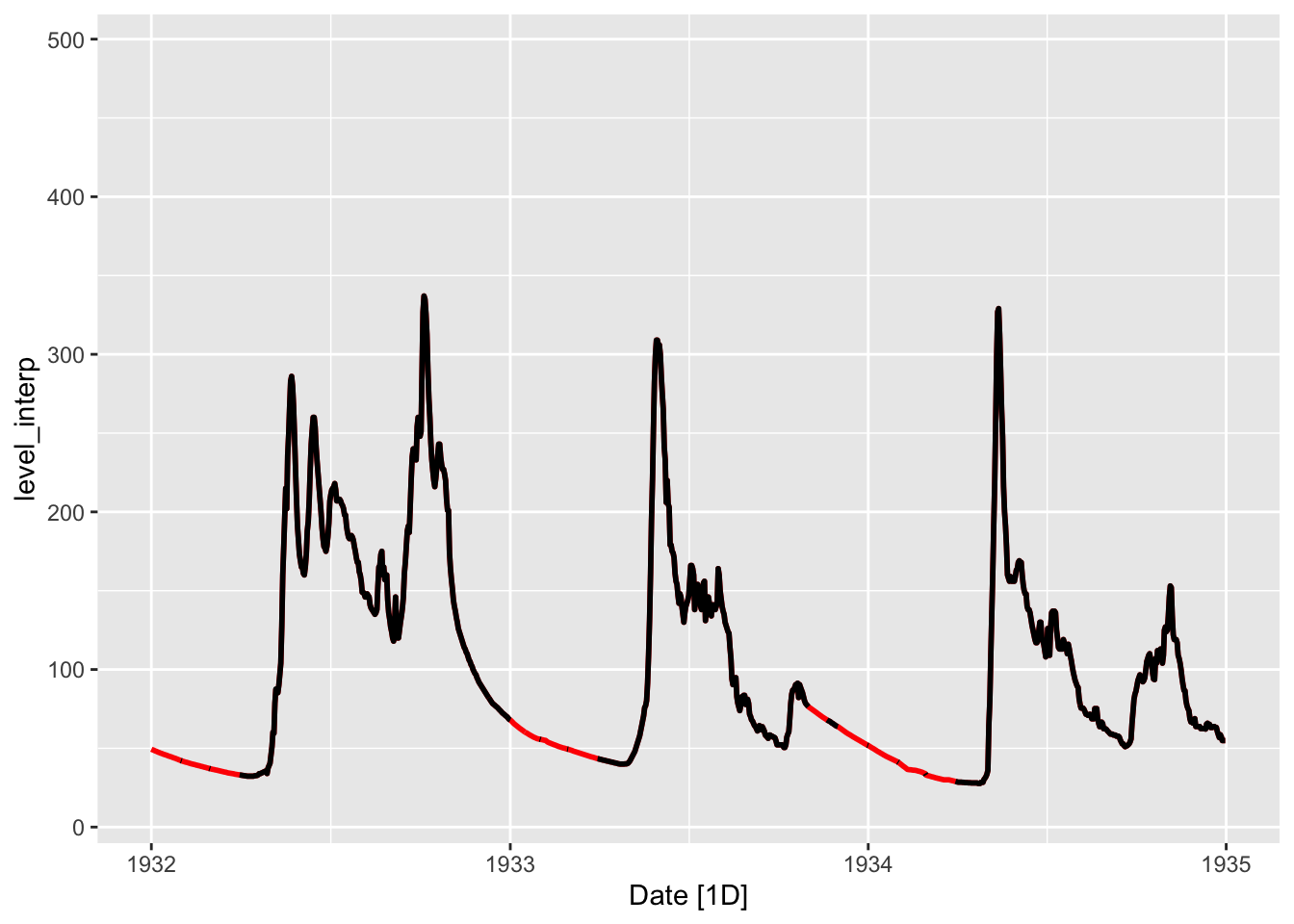

Аналогичного результата можно достичь с применением модели ARIMA, которая подыскивает наилучший интерполятор с учетом авторегрессии и сглаживающего среднего:

tsbl_int2 = tsbl |> 
  model(mdl = ARIMA(level ~ 0 + pdq(0,1,0) + PDQ(0,0,0))) |> 
  interpolate(tsbl)

autoplot(tsbl_int2, level, color = 'magenta', size = 1) +
  geom_line(aes(Date, level), tsbl, size = 1) +
  scale_x_date(limits = c(ymd(19320101), ymd(19350101)))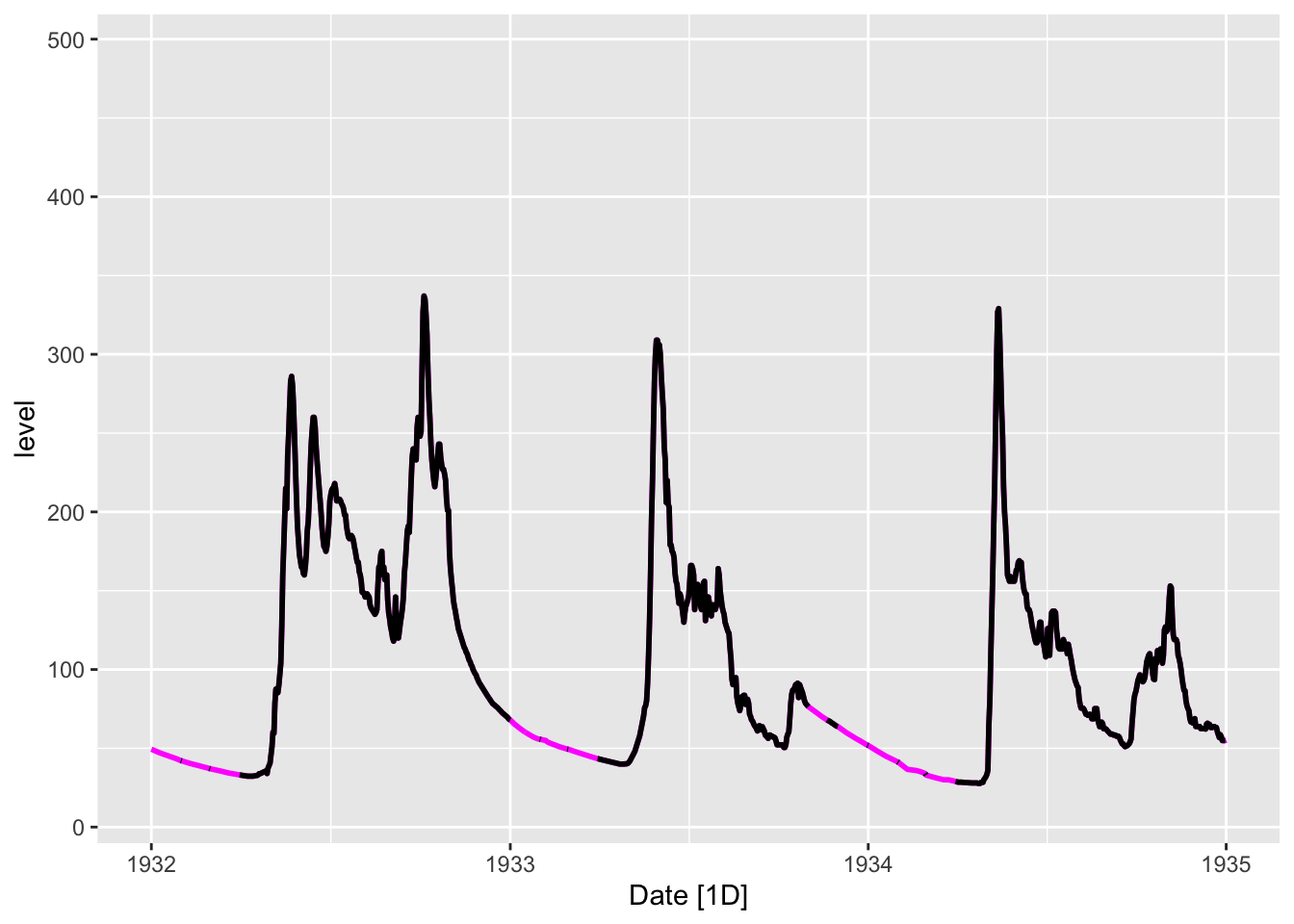

В заключение проведем заново оценку ситуации с пропусками в данных. Для этого необходимо привести данные к обычному классу tibble:

timerep_interp = find_gaps(tsbl_int, 'level_interp')

Аналогичная таблица, заполненная методом ARIMA, уже не имеет пропусков, поскольку не установлены временные ограничения на длину интервала интерполяции:

timerep_interp2 = find_gaps(tsbl_int2, 'level')

По результатам автокореляционного анализа и интерполяции удалось заполнить значительное число пропусков в данных. Однако по прежнему остаются значительные по длине пропуски, которые уже требуют привлечения дополнительных источников информации для их заполнения.

8.5 Интерполяция с учетом предикторов

В некоторых случая интерполяцию можно уточнить с использованием предикторов. Рассмотрим уточнение прогноза уровня воды с учетом информации о температурах и осадках на р. Умба:

meteo = read_delim('data/in_Umba_meteo.txt', delim = ' ', 
                 col_names = c('day', 'month', 'year', 'temp', 'prec'), na = '9999') |> 
  mutate(Date = ymd(paste(year, month, day)),
         tempsm = zoo::rollmean(temp, 10, fill = NA, align = 'center'),
         precsum = zoo::rollsum(prec, 5, fill = NA, align = 'center')) |> 
  select(Date, temp, tempsm, prec, precsum)

tsbl_all = left_join(tsbl_int, meteo, by = 'Date')
tsbl_all
# A tsibble: 30,316 x 10 [1D]
     day month  year level Date       level_interp   temp tempsm  prec precsum
   <dbl> <dbl> <dbl> <dbl> <date>            <dbl>  <dbl>  <dbl> <dbl>   <dbl>
 1     1     1  1932  49.4 1932-01-01         49.4 -14.9   NA    0.184   NA   
 2     2     1  1932  NA   1932-01-02         49.1 -15.1   NA    0.578   NA   
 3     3     1  1932  NA   1932-01-03         48.9 -10.4   NA    0.942    3.97
 4     4     1  1932  NA   1932-01-04         48.6  -7.58  NA    1.44     4.07
 5     5     1  1932  NA   1932-01-05         48.3  -8.46 -11.3  0.826    4.42
 6     6     1  1932  NA   1932-01-06         48.1 -13.0  -10.7  0.288    4.64
 7     7     1  1932  NA   1932-01-07         47.8 -13.3   -9.72 0.925    3.95
 8     8     1  1932  NA   1932-01-08         47.5 -10.4   -8.83 1.16     3.79
 9     9     1  1932  NA   1932-01-09         47.3 -10.4   -8.33 0.75     4.53
10    10     1  1932  47   1932-01-10         47    -9.16  -7.62 0.662    4.49
# ℹ 30,306 more rows

Расширим временной диапазон рассмотрения

autoplot(tsbl_all, level_interp, size = 1) +
  scale_x_date(limits = c(ymd(19320101), ymd(19360101)))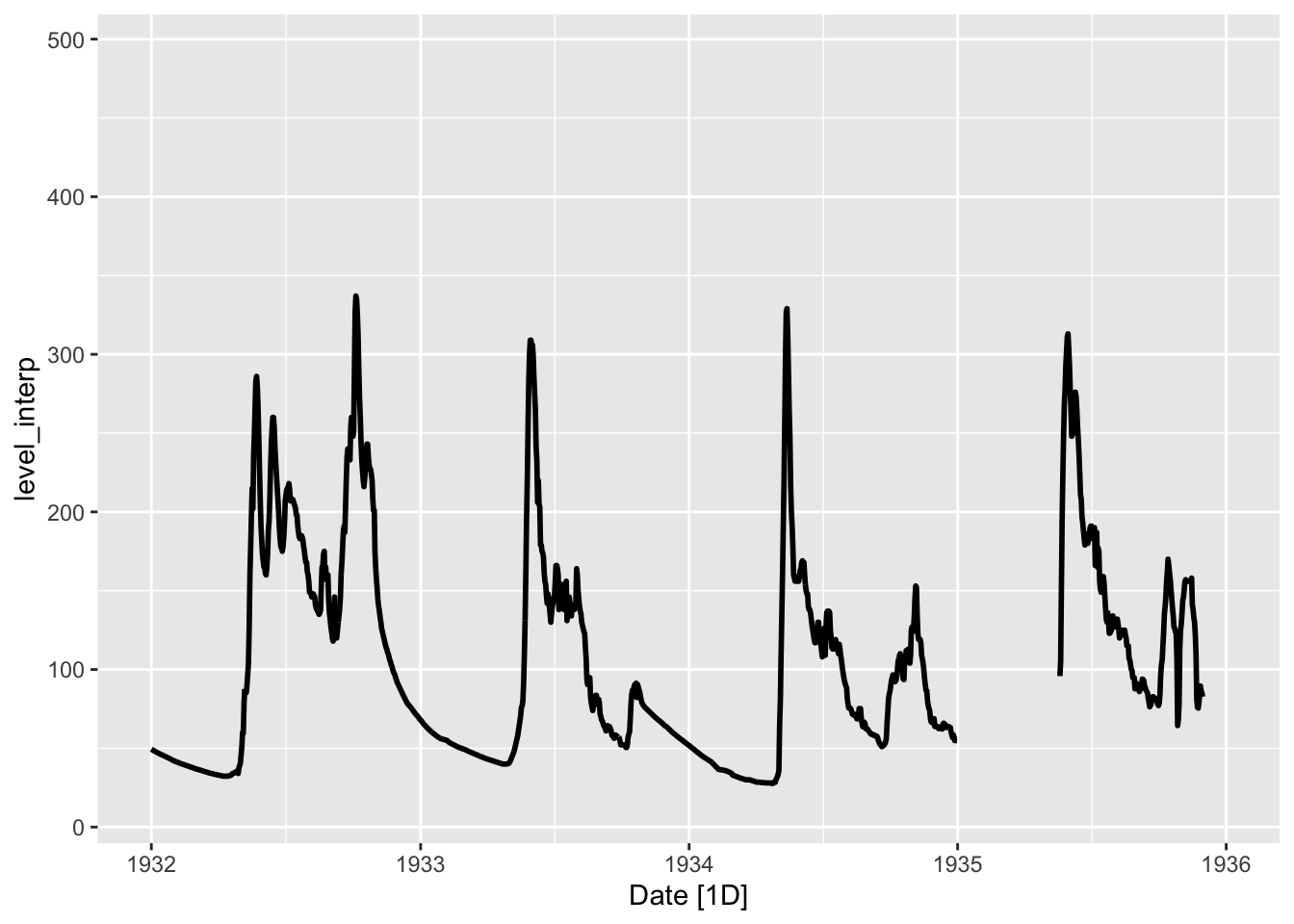

Видно, что период в начале 1935 года слишком длинный для того чтобы его прогнозировать с использованиме исключительно авторегрессионных свойств и сглаживающего среднего. Попробуем для этого применить связь с осадками и температурой:

tsbl_int_met = tsbl_all |> 
  model(mdl = ARIMA(level_interp ~ tempsm + precsum)) |> 
  interpolate(tsbl_all)

autoplot(tsbl_int_met, level_interp, color = 'green', size = 1) +
  geom_line(aes(Date, level_interp), tsbl_all, size = 1) +
  scale_x_date(limits = c(ymd(19320101), ymd(19360101)))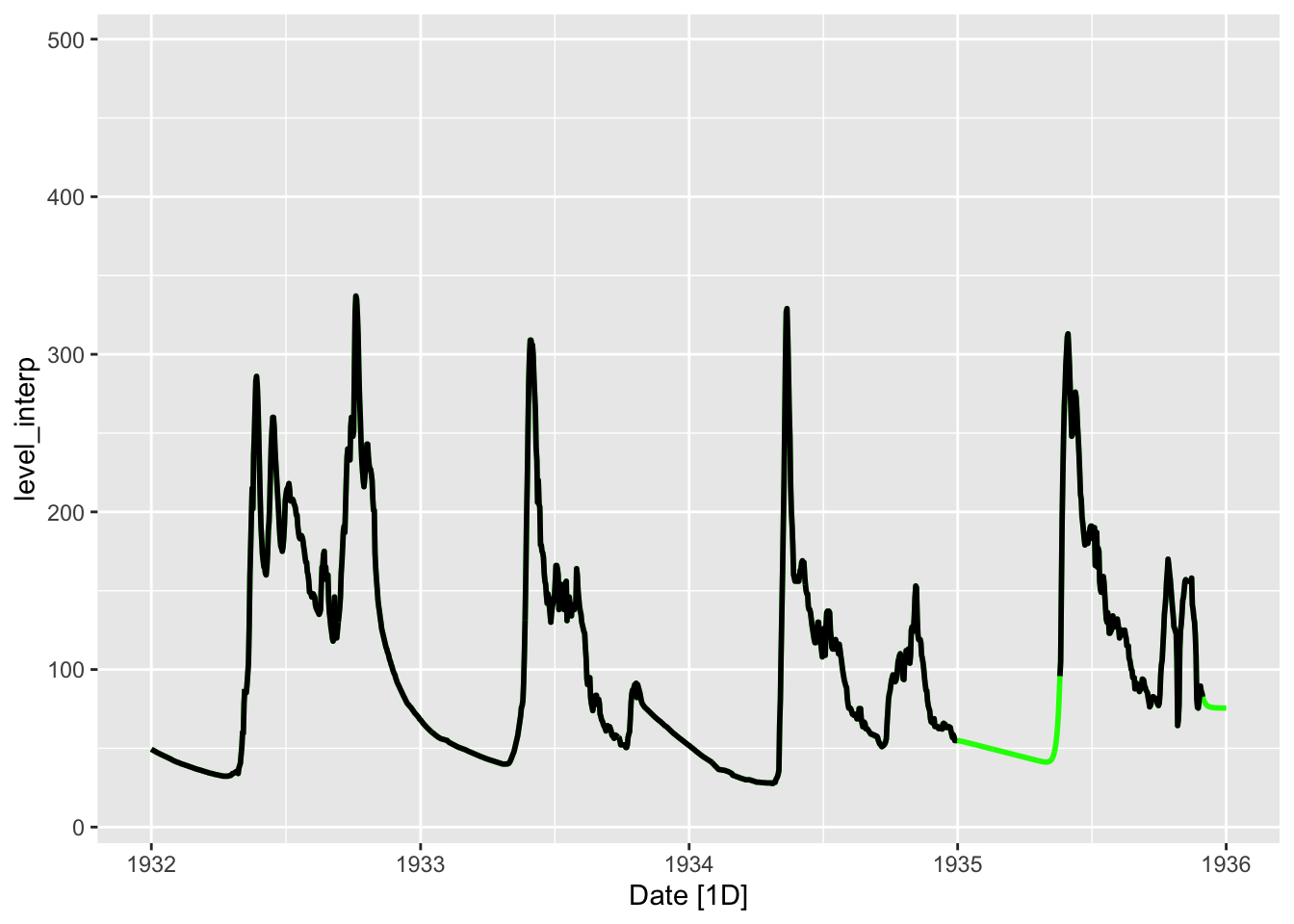

8.5.1 Пересчет на другую временную сетку

Когда данные, поступающие из различных источников, привязаны к несовпадающим временным срезам, возникает задача приведения их к единой временной сетке. Как правило, эта сетка имеет регулярный шаг (каждый час, каждый месяц и т.д.), поскольку это упрощает выполнение статистического анализа.

Одним из источников данных, не привязанных к жесткой временной сетке, является геосенсорная сеть домашних метеостанций NETATMO, которая собирает информацию с пользовательских устройств примерно каждый полчаса. Сроки, однако, четко не соблюдаются. Помимо этого, система, в силу её добровольно-волонтёрского характера, не предусматривает бесперебойное функционирование всех метеостанций: пользователь может отключить свой прибор на несколько часов или дней, в результате чего в данных могут образоваться дополнительные пропуски. Вследствие этого данные NETATMO характеризуются высокой степенью иррегулярности во времени.

Загрузим в качестве примера данные по метеостанции с идентификатором 70_ee_50_00_8e_1a, расположенной в пределах Московского мегаполиса (данные выгружены посредством NETATMO Weather API):

(tab = read_csv('data/70_ee_50_00_8e_1a.csv'))
# A tibble: 1,405 × 11
   altitude humidity id                latitude longitude pressure temperature
      <dbl>    <dbl> <chr>                <dbl>     <dbl>    <dbl>       <dbl>
 1      189       55 70:ee:50:00:8e:1a     55.7      37.6    1014.        23.1
 2      189       56 70:ee:50:00:8e:1a     55.7      37.6    1013.        22.5
 3      189       57 70:ee:50:00:8e:1a     55.7      37.6    1014.        21.9
 4      189       59 70:ee:50:00:8e:1a     55.7      37.6    1014.        21.1
 5      189       62 70:ee:50:00:8e:1a     55.7      37.6    1014         20  
 6      189       65 70:ee:50:00:8e:1a     55.7      37.6    1014.        19.7
 7      189       66 70:ee:50:00:8e:1a     55.7      37.6    1014.        19.6
 8      189       67 70:ee:50:00:8e:1a     55.7      37.6    1014.        19.5
 9      189       68 70:ee:50:00:8e:1a     55.7      37.6    1014.        19.2
10      189       68 70:ee:50:00:8e:1a     55.7      37.6    1015.        19.2
# ℹ 1,395 more rows
# ℹ 4 more variables: time_humidity <dttm>, time_pressure <dttm>,
#   time_temperature <dttm>, timezone <chr>

Визуальная инспекция данных подсказывает нам, что данные по температуре, влажности и давлению получены на произвольные сроки с дискретностью порядка \(30\) или \(60\) минут, при этом для всех трех метеопараметров эти сроки не совпадают:

Чтобы осуществлять совместный анализ этих данных, необходимо привести их к единой временной сетке. Временная плотность данных NETATMO позволяет сделать такую сетку через каждые \(30\) минут. Алгоритм интерполяции данных для каждой из характеристик будет следующий:

  1. Определить минимальное и максимальное время измерений и округлить их до ближайшего времени, кратного \(30\) минутам в большую (для минимального времени) и меньшую (для максимального времени) сторону.
  2. Сформировать последовательность временных срезов между полученными границами \(30\)-минутной серии.
  3. Интерполировать величину показателя на новую сетку.

Определим расчетные интервалы времени для каждой из характеристик:

tab = tab |> select(id, temperature, time_temperature)

tmin = ceiling_date(min(tab$time_temperature), 
                    unit = '30 minutes')
tmax = floor_date(max(tab$time_temperature), 
                  unit = '30 minutes')

В данном случае видно, что возможные границы сроков интерполяции для всех трех переменных совпадают, что несколько облегачает задачу. Проинтерполуруем данные на единую регулярную временную сетку через \(30\) минут, используя функцию approx() из базового R. По умолчанию данная функция использует линейную интерполяцию по ближайшим значениям до и после интерполируемого:

time_interp = tibble(
  datetime = seq(tmin, tmax, by = '30 min'),
  temp = round(approx(tab$time_temperature, 
                      tab$temperature, 
                      xout = datetime)$y, 1)
)

Надежность каждого интерполированного значения можно оценить, задав максимальную продолжительность интерполируемого интервала. Предположим, что она не должна превышать \(60\) минут:

idx = sapply(time_interp$datetime, \(x) match(TRUE, tab$time_temperature >= x))

time_interp = time_interp |> 
  mutate(before_time = datetime - tab$time_temperature[idx-1],
         after_time = tab$time_temperature[idx] - datetime,
         valid = after_time - before_time <= minutes(60))
summary(time_interp)
    datetime                        temp       before_time      
 Min.   :2019-09-04 14:30:00   Min.   : 0.60   Length:2049      
 1st Qu.:2019-09-15 06:30:00   1st Qu.: 8.00   Class :difftime  
 Median :2019-09-25 22:30:00   Median :11.00   Mode  :numeric   
 Mean   :2019-09-25 22:30:00   Mean   :11.63                    
 3rd Qu.:2019-10-06 14:30:00   3rd Qu.:15.20                    
 Max.   :2019-10-17 06:30:00   Max.   :24.90                    
  after_time         valid        
 Length:2049       Mode :logical  
 Class :difftime   FALSE:280      
 Mode  :numeric    TRUE :1769     
                                  
                                  
                                  
cat('Valid are ', round(100 * sum(time_interp$valid) / nrow(time_interp), 1), 
    '% of interpolated values', sep = '')
Valid are 86.3% of interpolated values

8.5.2 Прогнозирование по времени

Рассмотрим задачу прогнозирования количества потребляемой электроэнергии в штате Виктория (Австралия) в зависимости от температуры воздуха. Существует корреляция между этими переменными.

data(vic_elec, package = 'tsibbledata')

vic_elec_daily = vic_elec |> 
  filter(year(Time) == 2014) |> 
  index_by(Date = date(Time)) |> 
  summarise(
    Demand = sum(Demand) / 1e3,
    Temperature = max(Temperature),
    Holiday = any(Holiday)
  ) |> 
  mutate(Day_Type = case_when(
    Holiday ~ "Holiday",
    wday(Date) %in% 2:6 ~ "Weekday",
    TRUE ~ "Weekend"
  ))

vic_elec_daily |> 
  pivot_longer(c(Demand, Temperature)) |> 
    ggplot(aes(x = Date, y = value)) +
    geom_line() +
    facet_grid(name ~ ., scales = "free_y") + ylab("")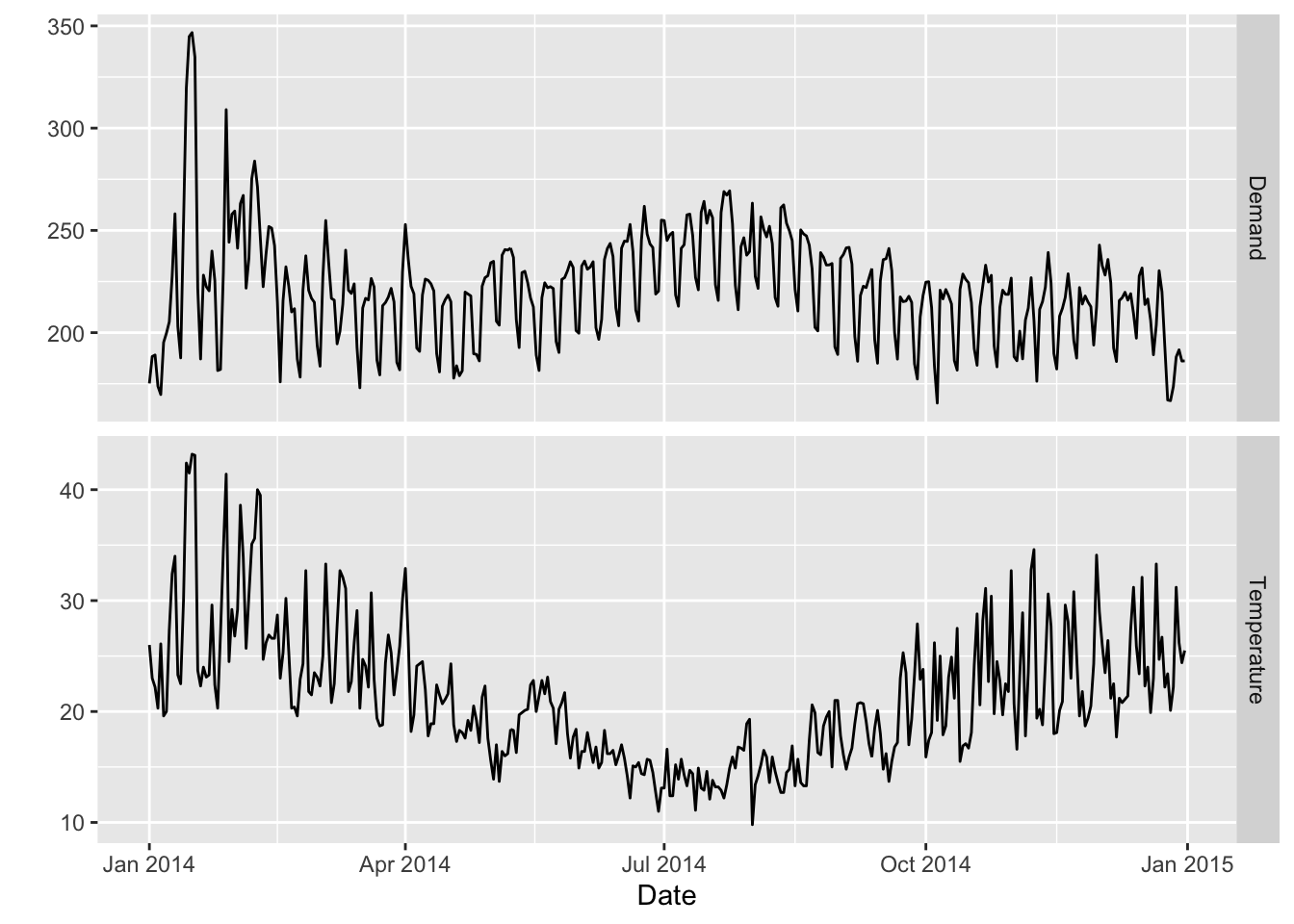

Выполним построение модели:

fit = vic_elec_daily |> 
  model(ARIMA(Demand ~ Temperature + I(Temperature^2) +
                (Day_Type == "Weekday")))

И прогнозирование:

vic_elec_future = new_data(vic_elec_daily, 14) |> 
  mutate(
    Temperature = 26,
    Holiday = c(TRUE, rep(FALSE, 13)),
    Day_Type = case_when(
      Holiday ~ "Holiday",
      wday(Date) %in% 2:6 ~ "Weekday",
      TRUE ~ "Weekend"
    )
  )

forecast(fit, vic_elec_future) |> 
  autoplot(vic_elec_daily) +
  labs(title="Daily electricity demand: Victoria",
       y="GW")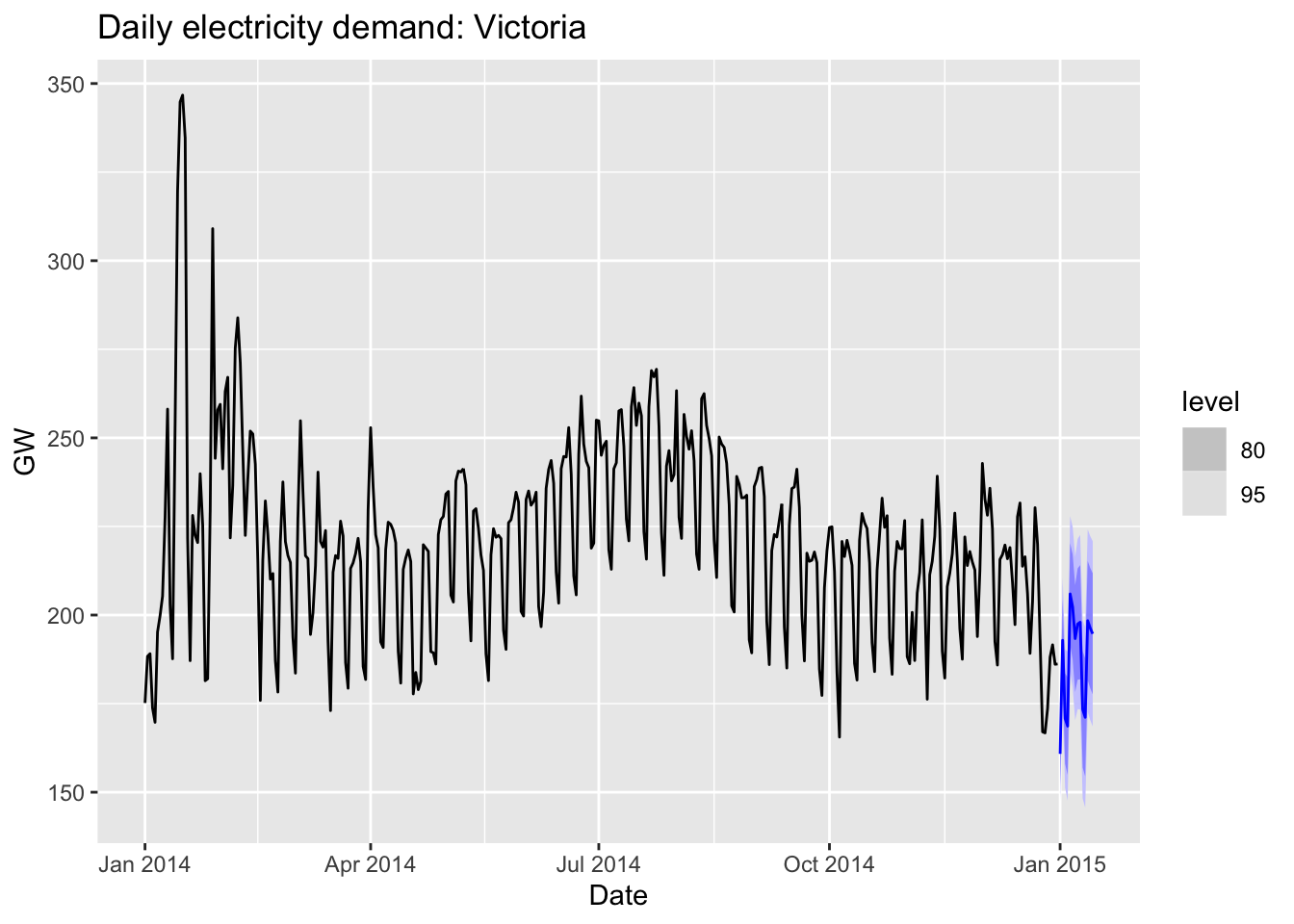

8.6 Аппроксимация по времени

Одной из важных составляющих работы с временными данными является анализ временных трендов и закономерностей. В качестве примера возьмем данные межгодичных изменений характеристик стока реки Мезень на посту Малонисогорская2:

(tab = read_csv('data/Mezen.csv'))
# A tibble: 75 × 57
   year_number Year1 Year2 datestart  datepolend    Qy  Qmax datemax     Qygr
         <dbl> <dbl> <dbl> <date>     <date>     <dbl> <dbl> <date>     <dbl>
 1           1  1938  1939 2000-03-23 2000-06-08  98.1   747 2000-04-03  19.9
 2           2  1939  1940 2000-03-16 2000-07-11  66.9   487 2000-04-28  14.8
 3           3  1940  1941 2000-03-09 2000-07-12  97.4   995 2000-04-28  18.9
 4           4  1941  1942 2000-03-24 2000-07-21 214.   2030 2000-05-01  31.4
 5           5  1942  1943 2000-04-02 2000-07-31 242.   2790 2000-05-08  26.9
 6           6  1943  1944 2000-03-24 2000-06-15  71.3   451 2000-05-02  26.5
 7           7  1944  1945 2000-02-26 2000-06-30  89.0   530 2000-04-28  27.0
 8           8  1945  1946 2000-03-25 2000-07-13 128.   1220 2000-04-27  33.9
 9           9  1946  1947 2000-03-15 2000-06-30 179.   2150 2000-04-28  25.8
10          10  1947  1948 2000-03-06 2000-07-15 153.   1720 2000-04-16  31.3
# ℹ 65 more rows
# ℹ 48 more variables: Qmmsummer <dbl>, monmmsummer <date>, Qmmwin <dbl>,
#   nommwin <date>, Q30s <dbl>, date30s1 <date>, date30s2 <date>, Q30w <dbl>,
#   date30w1 <date>, date30w2 <date>, Q10s <dbl>, date10s1 <date>,
#   date10s2 <date>, Q10w <dbl>, date10w1 <date>, date10w2 <date>, Q5s <dbl>,
#   date5s1 <date>, date5s2 <date>, Q5w <dbl>, date5w1 <date>, date5w2 <date>,
#   Wy <dbl>, Wgr <dbl>, Wpol1 <dbl>, Wpol2 <dbl>, Wpol3 <dbl>, Wpavs1 <dbl>, …

Построим график межгодичной изменчивости объема грунтового стока (переменная Wgr в \(км^3\)). Для того чтобы нанести линию глобального тренда, добавим грамматику geom_smooth(method = 'lm'):

ggplot(tab, mapping = aes(Year1, Wgr)) +
  geom_line() +
  geom_area(alpha = 0.5) +
  geom_smooth(method = 'lm') +
  labs(title = 'Объем грунтового стока на р. Мезень в д. Малонисогорская',
       x = 'Год',
       y = 'куб. км')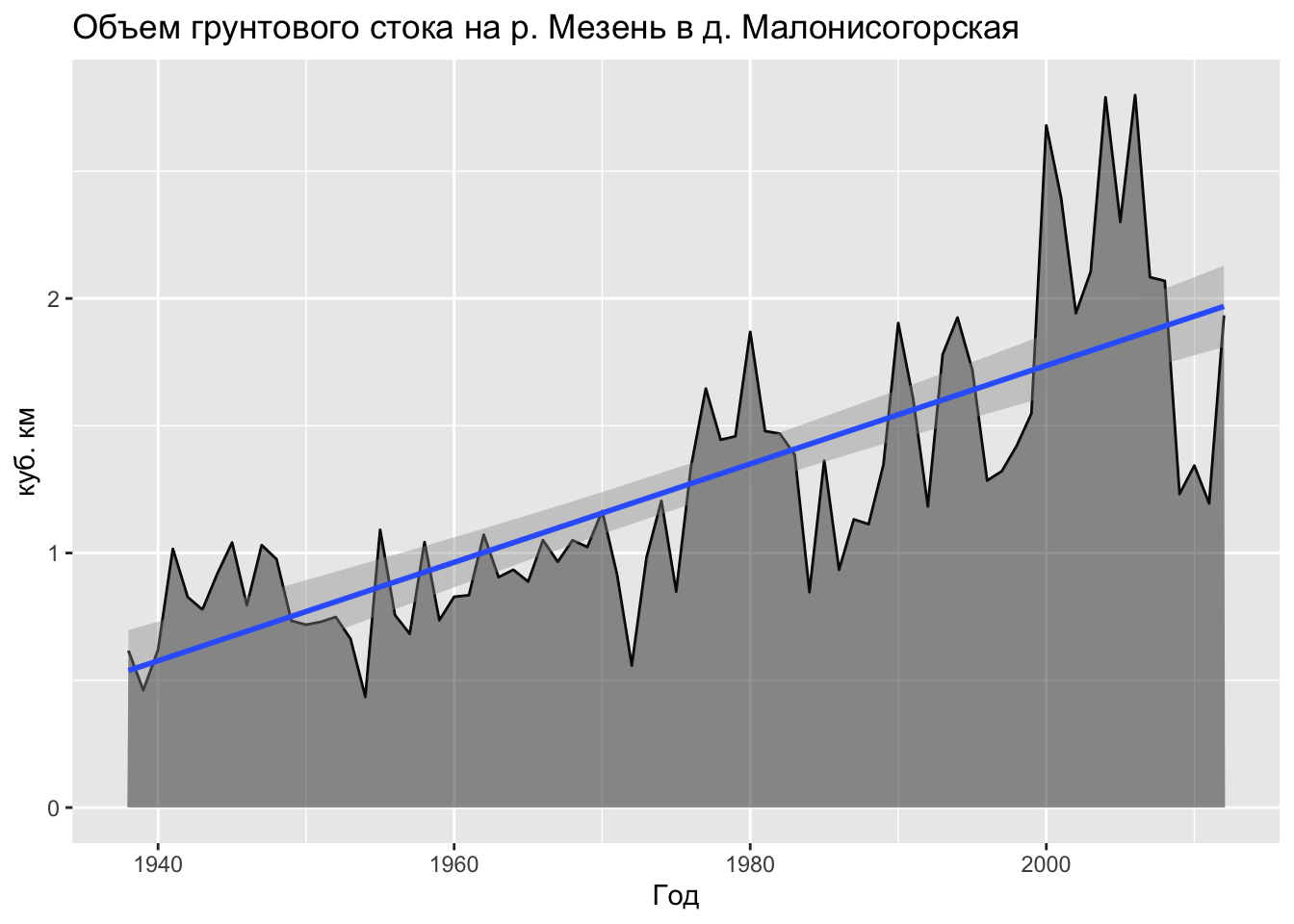

Как видно из данного графика, в масштабах десятилетий грунтовый сток имеет очевидный тренд на увеличение. В то же время, наблюдаяются колебания более короткого временного масштаба: серии годов повышенного стока сменяются годами более низкого стока. Чтобы графически выявить эти колебания, можно аппроксимировать исходный ряд данных с помощью кривой локальной регрессии. Для этого добавим грамматику geom_smooth() без параметров (это равносильно также вызову geom_smooth(method = 'loess')):

ggplot(tab, mapping = aes(Year1, Wgr)) +
  geom_line() +
  geom_area(alpha = 0.5) +
  geom_smooth(method = 'lm') +
  geom_smooth(color = 'orangered', span = 0.2) +
  labs(title = 'Объем грунтового стока на р. Мезень в д. Малонисогорская',
       x = 'Год',
       y = 'куб. км')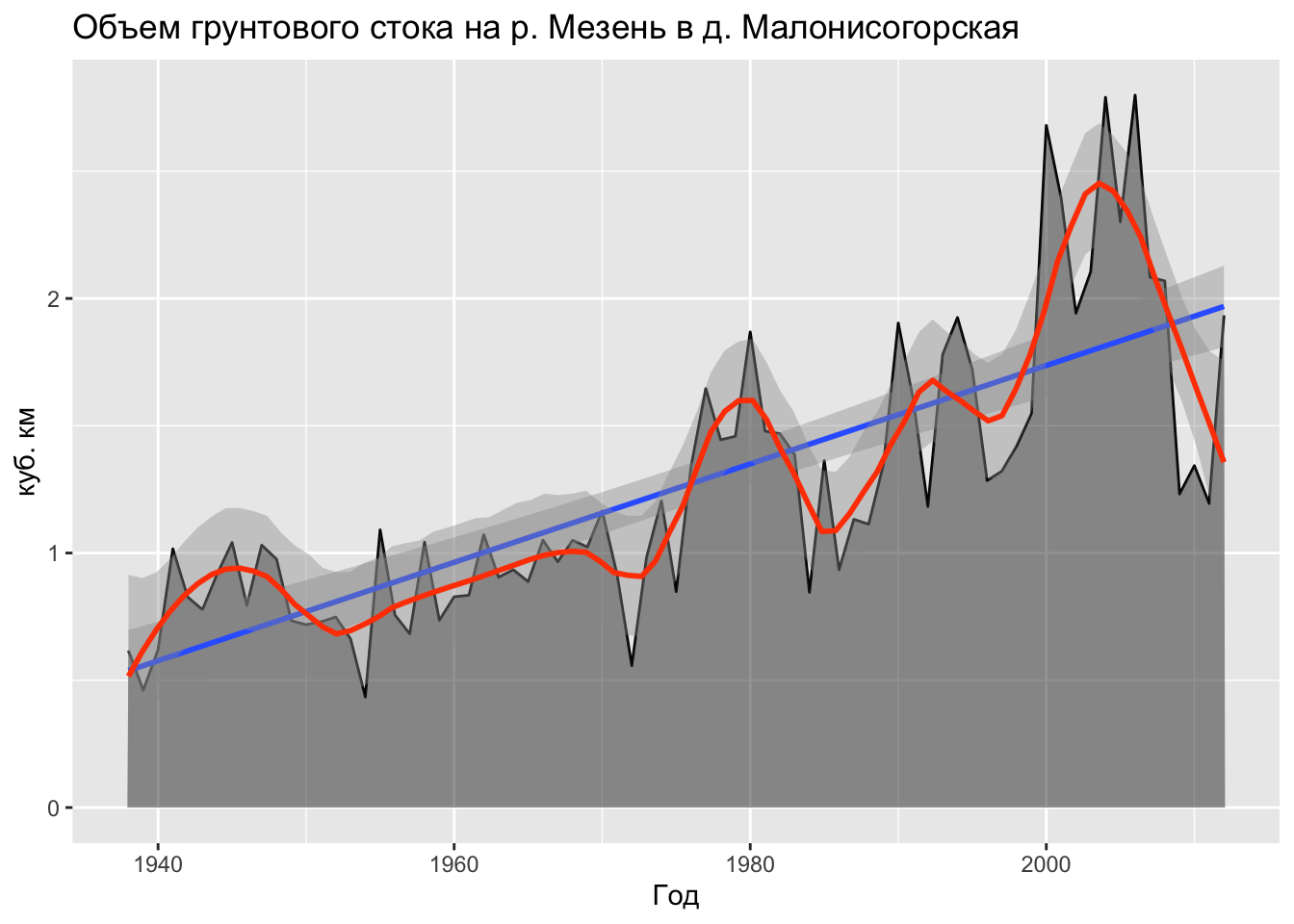

Метод локальной регрессии изначально был разработан для построения кривых регрессии в случае когда зависимость между переменными ведет себя сложным образом и не может быть описана в терминах традиционной линейной и нелинейной регрессии — глобальных методов. В этом случае область значений независимой переменной \(X\) можно покрыть конечным числом отрезков, для каждого из которых далее находят регрессию традиционным методом — как правило, линейную или квадратичную. Данный метод получил название LOWESS (Locally weighted scatterplot smoothing). В дальнейшем эта аббревиатура была редуцирована до LOESS.

В классической постановке метод LOESS реализуется следующим образом (Cleveland 1979). Пусть дано \(n\) точек исходных данных с координатами \(x\) (независимая переменная) и \(y\) (зависимая). Задается число \(0 < \alpha \leq 1\), которое обозначает долю от общего количества точек \(n\), выбираемую в окрестности каждой точки для построения регрессии. В абсолютном исчислении количество ближайших точек будет равно \(r = [\alpha n]\), где \([\cdot]\) — округление до ближайшего целого.

Тогда вес, который будет иметь каждая \(k\)-я точка исходных данных в уравнении регрессии для \(i\)-й точки исходных данных будет определяться по формуле:

\[w_k (x_i) = W\big((x_k - x_i)h_i^{-1}\big),\]

где \(h_i\) — расстояние до \(r\)-го по близости соседа точки \(x_i\), а \(W\) — весовая функция, отвечающая следующим условиям:

  1. \(W(x) > 0\) если \(|x| < 1\);
  2. \(W(-x) = W(x)\);
  3. \(W(x)\) невозрастающая функция для \(x \geq 0\);
  4. \(W(x) = 0\) если \(|x| \geq 1\).

Одним из стандартных вариантов весовой функции является “трикубическая” функция, определяемая как:

\[ W(x) = \begin{cases} (1 - |x|^3)^3, & \text{если } |x| < 1, \\ 0, & \text{если } |x| \geq 1. \end{cases} \]

Согласно определению весовой функции более близкие к \(x_i\) точки оказывают большее влияние на коэффициенты регрессии. Помимо этого за пределами расстояния \(h_i\) веса всех точек исходных данных будут обнуляться.

Сглаженная оценка \(\hat{y}_i\) в точке \(x_i\) получается в виде полинома степени \(d\):

\[\hat{y}_i = \sum_{j=0}^d \hat{\beta}_j (x_i) x_i^j,\] где коэффициенты \(\hat{\beta}_j\) находятся методом наименьших квадратов путем минимизации ошибки:

\[\sum_{k=1}^n w_k (x_i) (y_k - \beta_0 - \beta_1 x_k - ... - \beta_d x_k^d)^2\] Процедура поиска коэффициентов регрессии повторяется для каждой из \(n\) точек.

В методе LOESS используются степени регрессии \(d = 0, 1, 2\). Кубические и более высокие степени полиномов на практике не применяются. При степени равной 0 метод носит название сглаживающего среднего. Для построения линии локальной регрессии используйте функцию geom_smooth() без параметра method или с явным указанием параметра method = 'loess':

ggplot(data, aes(t, y)) +
  geom_point() +
  geom_smooth()

При визуализации линии локальной регрессии ggplot автоматически добавляет доверительные интервалы, показывающие диапазон нахождения искомой регрессионной кривой с вероятностью 0,95. Вы можете регулировать поведение локальной регрессии, задавая параметры n (количество ближайших точек \(r\)), span (доля ближайших точек \(\alpha\)) и formula (формула аппроксимируемой зависимости). По умолчанию используется регрессия первой степени (formula = y ~ x), значения n = 80 и span = 0.75. Вы можете их изменить, например задать более компактный охват для поиска коэффициентов. В этом случае кривая будет более чувствительна к локальному разбросу элементов выборкию. Нанесем несколько кривых локальной регрессии, используя разный охват данных:

ggplot(tab, mapping = aes(Year1, Wgr)) +
  geom_line() +
  geom_area(alpha = 0.5) +
  geom_smooth(color = 'yellow', span = 0.1) +
  geom_smooth(color = 'orangered', span = 0.2) +
  geom_smooth(color = 'darkred', span = 0.4) +
  labs(title = 'Объем грунтового стока на р. Мезень в д. Малонисогорская',
       x = 'Год',
       y = 'куб. км')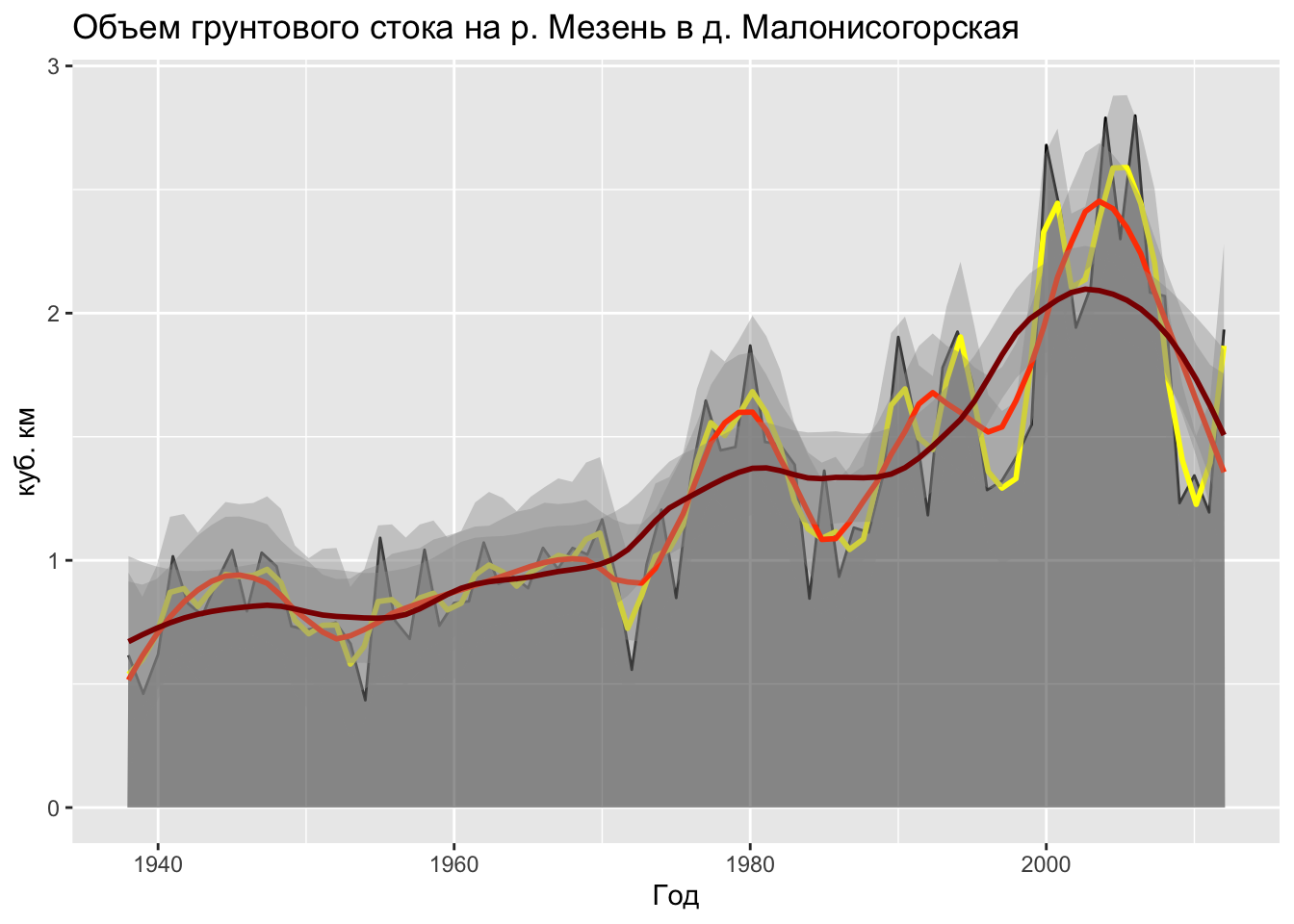

Видно, что при увеличении охвата локальная регрессия начинает отрадать колебания более крупного временного масштаба, но при этом хуже отражает реальный разброс значений, что приблажает ее к глобальной регрессии.

Вместо координат исходных точек для построения регрессии можно использовать и произвольные координаты \(X\). В этом случае кривая будет соединять точки, полученные локальной регрессионной оценкой в заданных координатах \(X\). Именно этот принцип используется в двумерном (и многомерном) случае. Пусть даны измерения показателя в \(N\) исходных точках и задано число \(\alpha\) — сглаживающий параметр. Тогда аппроксимация показателя в каждом узле интерполяции получается путем построения поверхности тренда (см. выше) по \(\alpha N\) ближайшим исходным точкам. Как и в одномерном случае, близкие точки будут оказывать более сильное влияние на коэффициенты регрессии, чем удаленные.

Метод LOESS предоставляет широкие возможности настройки благодаря вариативности параметра сглаживания и степени регрессионного полинома.

8.7 Статистики

Существует ряд статистик и статистических тестов, которые часто используются для временных данных. Среди них мы рассмотрим следующие:

  • Тест Манна-Кендалла на значимость линейного тренда
  • Тест Петтитт на точку перелома — Оценка тренда по методу Тейла-Сена

Для выполнения тестов Манна-Кендалла, Петтитт и оценки тренда по методу Тейла-Сена для объема грунтового стока Мезеня подключим пакет trend:

(mk = mk.test(tab$Wgr))

    Mann-Kendall trend test

data:  tab$Wgr
z = 7.8129, n = 75, p-value = 5.589e-15
alternative hypothesis: true S is not equal to 0
sample estimates:
           S         varS          tau 
1.709000e+03 4.779167e+04 6.158559e-01 
(pt = pettitt.test(tab$Wgr))

    Pettitt's test for single change-point detection

data:  tab$Wgr
U* = 1324, p-value = 4.131e-11
alternative hypothesis: two.sided
sample estimates:
probable change point at time K 
                             38 
(ts = sens.slope(tab$Wgr))

    Sen's slope

data:  tab$Wgr
z = 7.8129, n = 75, p-value = 5.589e-15
alternative hypothesis: true z is not equal to 0
95 percent confidence interval:
 0.01378903 0.02202750
sample estimates:
Sen's slope 
 0.01810404

Все три теста в данном случе дают высокую статистическую значимость временных изменений (p-значения), при этом тест Петтитт говорит, что точка перелома находится в 38-й позиции ряда. Если разделить исследуемый временной ряд на две выборки этой точкой, то они будут иметь статистически значимое отличие в характеристиках среднего значения показателя. Метод Тейла-Сена также говорит нам, что грунтовый сток увеличивается ежегодно примерно на \(1.8\%\) (величина тренда равна \(0.0181\)), что за период 70 лет даёт абсолютный прирост грунтового стока более чем в 2 раза.

Для наглядности нанесем полученную точку перелома на график:

ggplot(tab, mapping = aes(Year1, Wgr)) +
  geom_line() +
  geom_area(alpha = 0.5) +
  geom_smooth(method = 'lm', color = 'red') +
  geom_vline(xintercept = tab$Year1[pt$estimate], color = "red", size = 0.5) +
  annotate("text", label = tab$Year1[pt$estimate], 
           x = tab$Year1[pt$estimate] + 4, y = max(tab$Wgr), 
           size = 4, colour = "red") +
  labs(title = 'Объем грунтового стока на р. Мезень в д. Малонисогорская',
     x = 'Год',
     y = 'куб. км')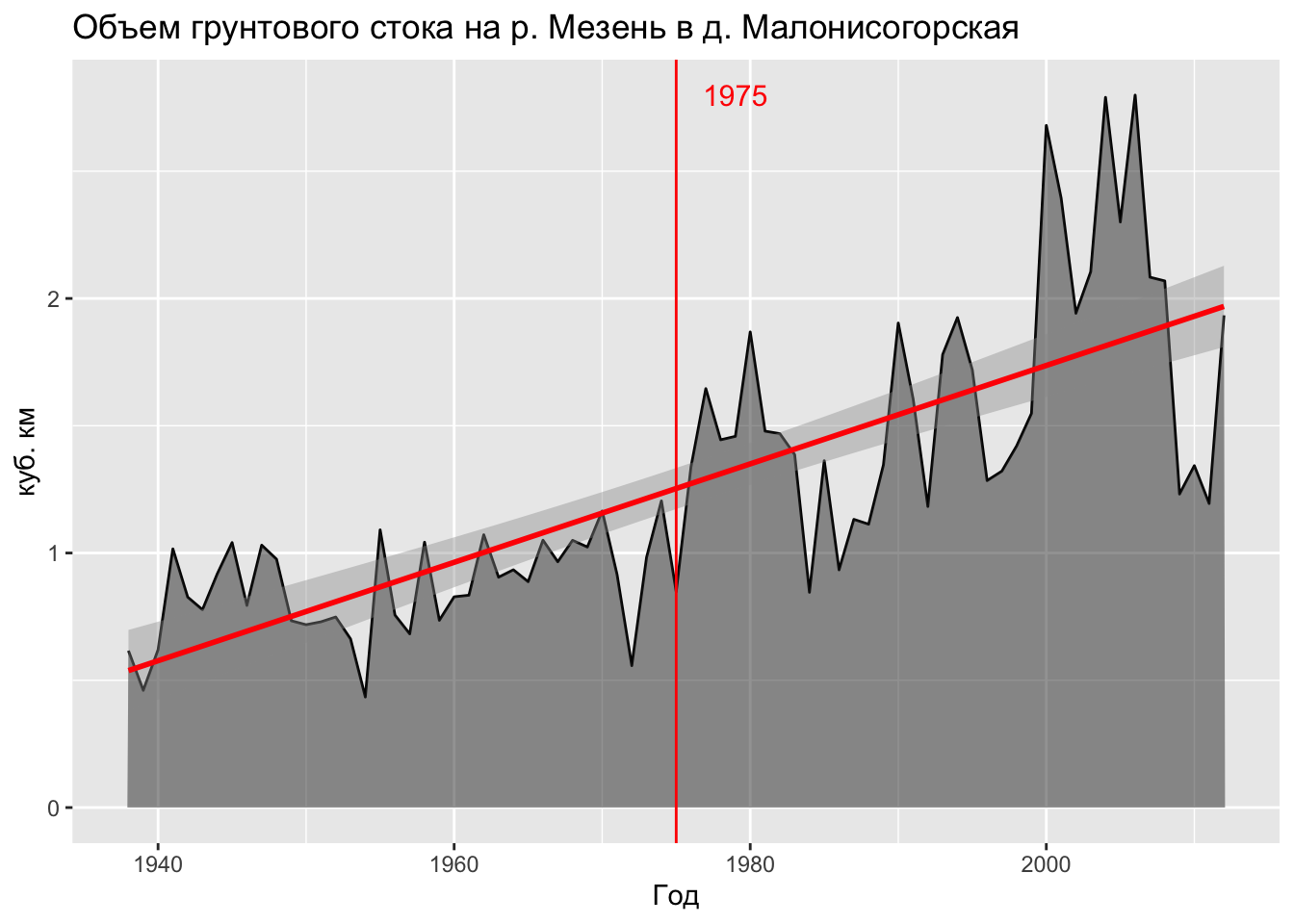

8.8 Анимация

Анимационная графика возволяет наглядно визуализировать изменения. Наиболее часто речь идет об изменениях по времени. В этом случае время работает в роли невидимой переменной, которая влияет на положение графических примитивов на изображении. Данный подход органично вписывается в концепцию грамматики графики, на основе которой построен пакет ggplot2 (см. Главу @ref(advgraphics)). Соответствующую реализацию грамматики анимаций предоставляет пакет gganimate(R-gganimate?).

Возможности анимаций в gganimate реализуются посредством добавления новых грамматик к построенному графику ggplot2. К числу этих грамматик относятся:

  • transition_*() — распределение данных по времени;
  • view_*() — поведение осей координат во времени;
  • shadow_*() — отображение данных, не относящихся к текущему временному срезу;
  • enter_*()/exit_*() — характер появления/исчезновения данных в процессе анимации;
  • ease_aes() — порядок смягчения (интерполяции) графических переменных в моменты перехода.

В качестве первого примера используем уже знакомые нам данные реанализа NASA POWER суточного осреднения, выгрузив информацию по точкам в трех городах (Мурманск, Москва, Краснодар) за 2018 год:

# TODO: set eval = TRUE after NASA POWER server is available
cities = list(
  Мурманск = c(33, 69),
  Москва = c(38, 56),
  Краснодар = c(39, 45)
)

tab = purrr::imap(cities, function(coords, city){
  get_power(
    community = "AG",
    lonlat = coords,
    pars = c("RH2M", "T2M", "PRECTOT"),
    dates = c("2018-01-01", "2018-12-31"),
    temporal_average = "DAILY"
  ) |> mutate(CITY = city,
               MONTH = month(YYYYMMDD))
}) |> bind_rows()

8.8.1 Переход по времени

Рассмотрим колебания температуры по 12 месяцам посредством диаграммы размаха, реализовав анимационный переход по времени посредством функции transition_time(). Текущий временной срез передается в переменную окружения frame_time, которая подается в подзаголовок графика (см параметр subtitle функции labs()):

ggplot(tab, aes(CITY, T2M)) +
  geom_boxplot() +
  labs(title = "Температура воздуха в 2018 году по данным NASA POWER",
       subtitle = 'Месяц: {round(frame_time)}') +
  xlab('Город') +
  ylab('Т, °С') +
  transition_time(MONTH)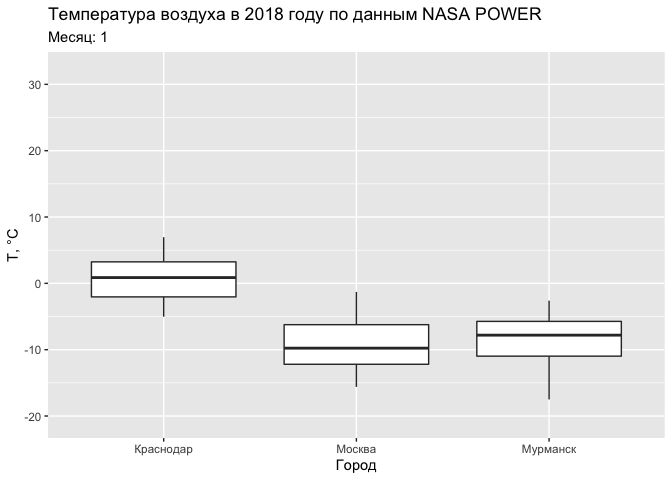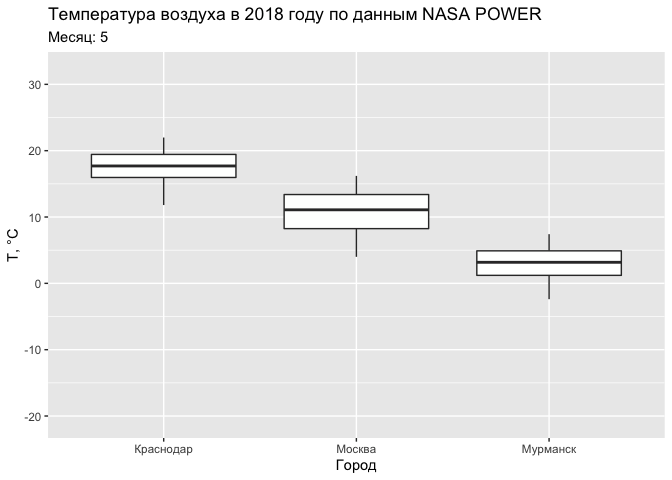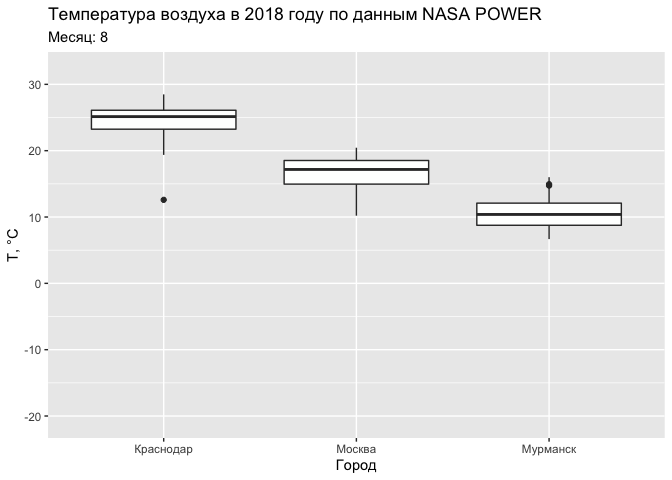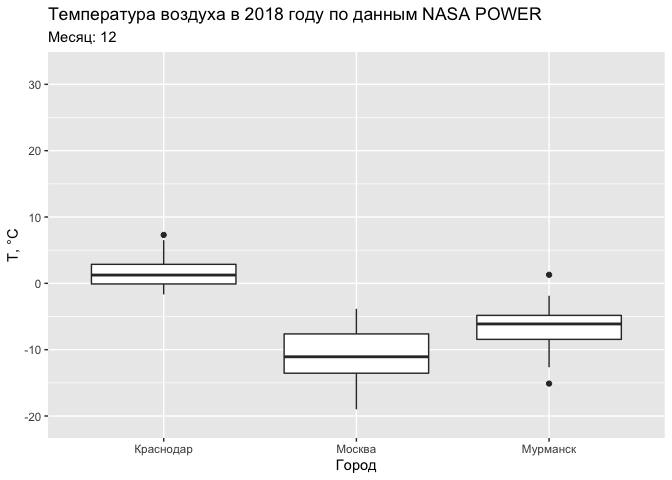

Текущий срез при выполнении анимации по времени доступен в переменной окружения frame_time.

Аналогичную анимацию можно провести и на примере функции плотности распределения:

ggplot(tab, aes(T2M, fill = CITY)) +
  geom_density(alpha = 0.5) +
  labs(title = "Температура воздуха в 2018 году по данным NASA POWER",
       subtitle = 'Месяц: {round(frame_time)}',
       fill = 'Город') +
  xlab('Т, °С') +
  ylab('Плотность распределения') +
  transition_time(MONTH)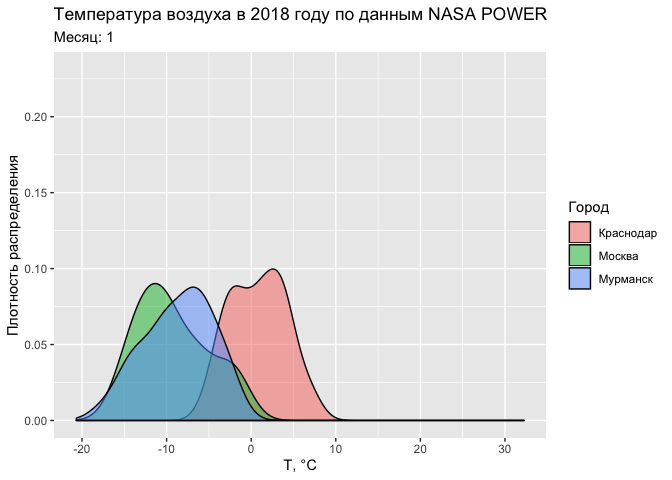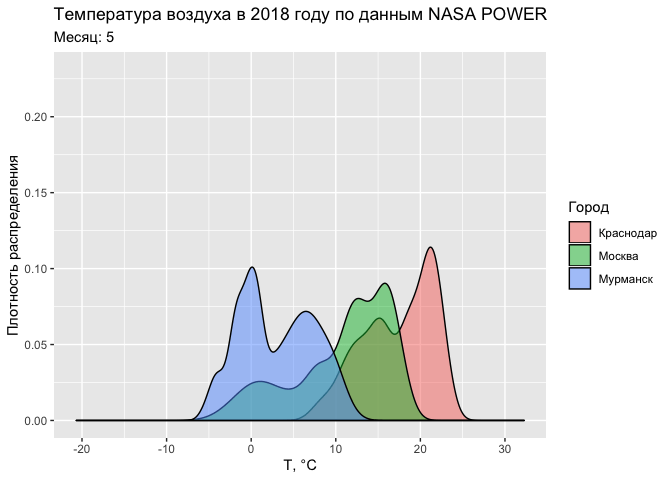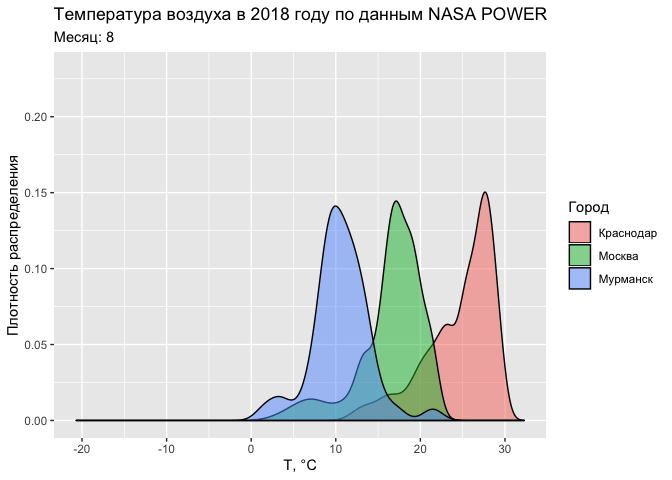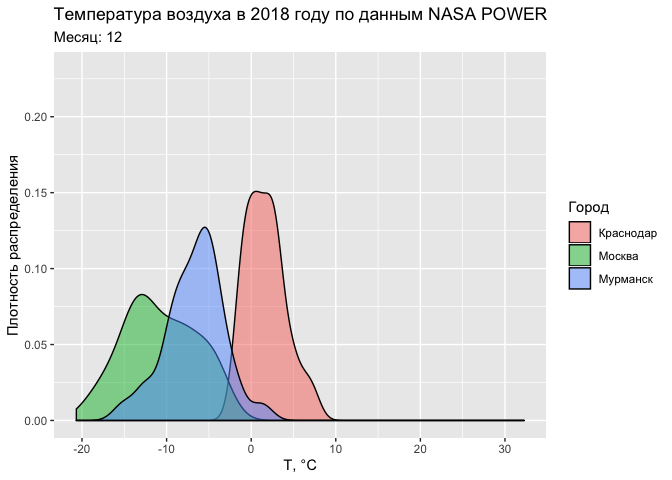

Загрузим ранее использованные в Главе @ref(stat_analysis) данные Gapminder по соотношению продолжительности жизни и ВВП на душу населения, но на этот раз не будем фильтровать их по времени:

countries = read_excel('data/gapminder.xlsx', 2) |>
  select(Country = name, Region = eight_regions) |>
  mutate(Country = factor(Country, levels = Country[order(.$Region)]))

gdpdf_tidy = read_sheet('1cxtzRRN6ldjSGoDzFHkB8vqPavq1iOTMElGewQnmHgg') |> ### ВВП на душу населения
  pivot_longer(cols = `1764`:`2018`, names_to = 'year', values_to = 'gdp') |> 
  rename(Country = 1)

popdf_tidy = read_sheet()'1IbDM8z5XicMIXgr93FPwjgwoTTKMuyLfzU6cQrGZzH8') |> # численность населения
  pivot_longer(cols = `1800`:`2015`, names_to = 'year', values_to = 'pop') |> 
  rename(Country = 1)

lifedf_tidy = read_sheet('1H3nzTwbn8z4lJ5gJ_WfDgCeGEXK3PVGcNjQ_U5og8eo') |> # продолжительность жизни
  pivot_longer(cols = `1800`:`2016`, names_to = 'year', values_to = 'lifexp') |> 
  rename(Country = 1)

tab = gdpdf_tidy |> 
  inner_join(lifedf_tidy) |> 
  inner_join(popdf_tidy) |> 
  inner_join(countries) |> 
  mutate(year = as.integer(year)) |> 
  drop_na()

Теперь чтобы отобразить это соотношение в виде анимации, достаточно добавить новый переход по времени:

options(scipen = 999) # убираем экспоненциальную форму записи числа
ggplot(tab, aes(gdp, lifexp, size = pop, color = Region)) +
  geom_point(alpha = 0.5) +
  scale_x_log10() +
  labs(title = 'Year: {round(frame_time)}') +
  theme_bw() +
  transition_time(year)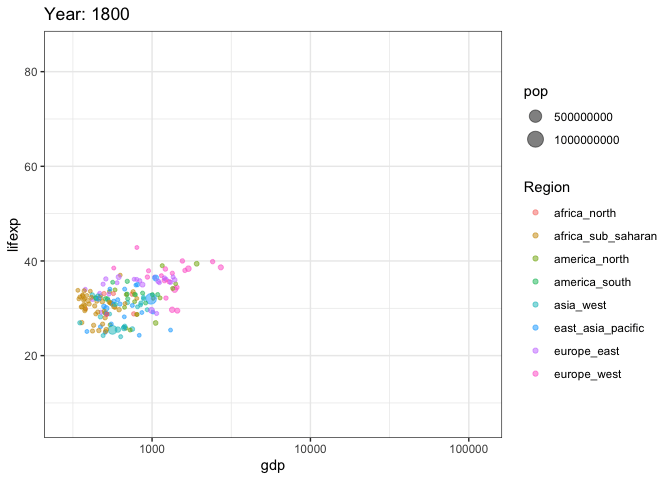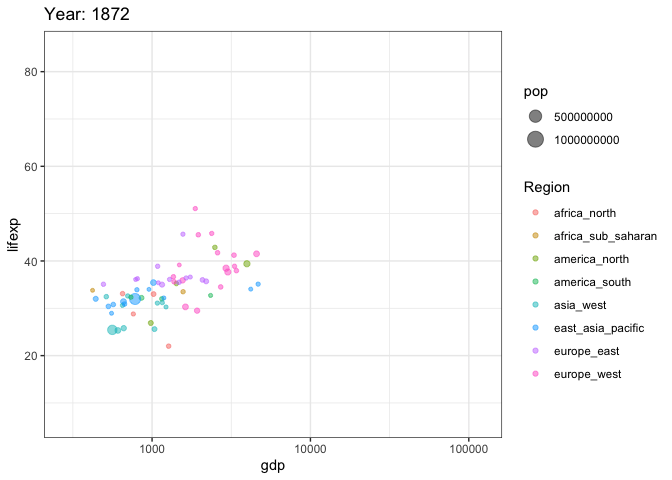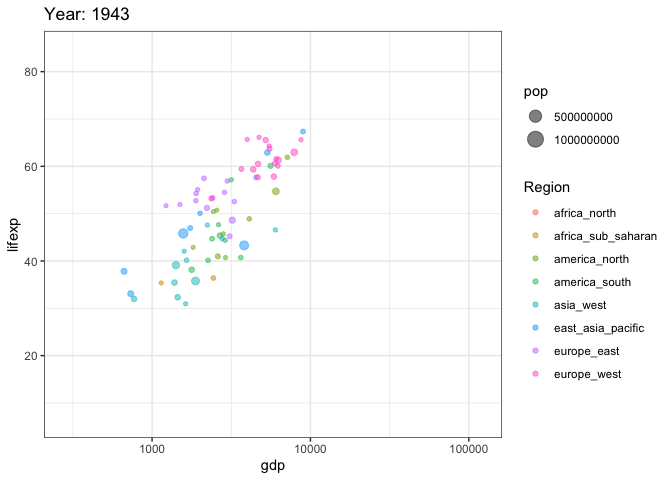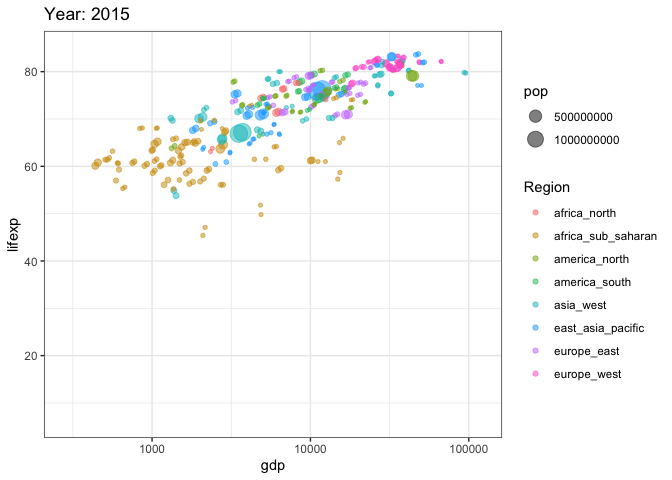

8.8.2 Переход по состояниям

В ряде случаев вместо перехода по времени целесообразно использовать переход по состояниям. В частности, такой подход оказывается удобен, когда сопоставляются данные за аналогичные временные срезы разных периодов. Например, 12 часов каждого дня недели с анимацией по неделям. Либо каждый день года с анимацией по годам. В этом случае координаты X будут фиксированы, а значение Y будет зависить от текущего состояния.

Подобную стратегию можно использовать для визуализации изменений внутригодичного распределения величины между годами. Примером таких изменений являются данные о расходах воды на гидропосте Паялка, рассмотренные нами ранее в настоящей главе. В качестве результата мы хотим видеть анимацию гидрографа реки, в которой каждый кадр соответствует календарному году.

Для составления такой анимации необходимо сначала убедиться, что в данных все года заполнены корректно (не пусты), и что нет годов, за которые вообще нет данных (такие года придется из анимации исключить, так как для них гидрограф построить невозможно). Помимо этого, чтобы обеспечить сопоставимость аналогичных дат за разные года, необходимо сохранить у них только месяц и день. Поскольку такого формата даты не существует, в качестве “трюка” можно просто заменить года всех дат на \(2000\) и записать результат в новое поле. Необходимые преобразования реализуются следующим образом:

flt_tab = tsbl_int |> 
  filter(!is.na(year)) |> 
  group_by(year) |>
  filter(!all(is.na(level_interp))) |> 
  ungroup() |> 
  mutate(yDate = Date)

year(flt_tab$yDate) <- 2000 # фиктивное поле, в котором аналогичные даты за разные года совпадают

После выполнения необходимой подготовки таблица данных готова для анимации. Переход по состояниям реализуется посредством вызова функции transition_states(), при этом параметр state_length = 0 обеспечивает плавность анимации за счет нулевой задержки в каждом состоянии. Полученный график предварительно сохраняется в промежуточную переменную anim, чтобы в дальнейшем можно было управлять качеством анимации путем вызова функции animate(). В частности, мы устанавливаем общее число кадров в \(10\) раз больше количества состояний (годов), чтобы обеспечить плавный переход между ними посредством интерполяции (tweening), автоматически выполняемой функцией animate() между кадрами:

anim = ggplot(flt_tab, mapping = aes(x = yDate, y = level_interp)) +
    geom_ribbon(aes(ymin = 0, ymax = level_interp), alpha = 0.5) +
    geom_line() +
    scale_x_date(date_breaks = "1 month", date_labels = "%b") +
    labs(title = "Расход воды на гидропосту Паялка (р. Умба, Мурманская обл.)",
         subtitle = 'Год: {closest_state}') +
    xlab('Дата') +
    ylab('куб.м/с') +
    theme(text = element_text(size = 18, family = 'Open Sans')) +
    transition_states(year, state_length = 0) +
    view_follow(fixed_y = TRUE)

animate(anim, 
        fps = 20,                                    # число кадров в секунду
        nframes = 10 * length(unique(flt_tab$year)), # общее число кадров
        width = 800, 
        height = 600)

Текущий срез при выполнении анимации по состояниям доступен в переменной окружения closest_state.

В настоящей главе мы рассмотрели лишь базовые возможности создания анимаций средствами пакета gganimate. Более подробно с другими возможностями пакета можно ознакомиться в справочнике по его функциям.

8.9 Краткий обзор

Для просмотра презентации щелкните на ней один раз левой кнопкой мыши и листайте, используя кнопки на клавиатуре:

Презентацию можно открыть в отдельном окне или вкладке браузере. Для этого щелкните по ней правой кнопкой мыши и выберите соответствующую команду.

8.10 Контрольные вопросы и упражнения

8.10.1 Вопросы

  1. Назовите типы данных, использующиеся для представления дат и времени в R.
  2. Какая дата является началом эпохи UNIX, используемой в качестве нулевой точки отсчета времени?
  3. Какая функция может быть использована для расчета разности дат и времени?
  4. В чем разница между функциями day() и yday() в пакете lubridate?
  5. Чем отличаются периоды и длительности в lubridate?
  6. Если вам нужно прибавить к дате требуемое количество лет, месяцев, недель или дней, то какими функциями вы бы воспользовались?
  7. Что из себя представляет автокорреляционная функция и каким образом она вычисляется в R?
  8. Что из себя представляет кусочно-линейная функция и каким образом она вычисляется в R?
  9. Какая функция пакета zoo позволяет заполнять отсутствующие значения линейной интерполяцией?
  10. В чем суть метода локальной регрессии? Как его можно использовать при исследовании временных рядов?
  11. Какие параметры geom_smooth() можно использовать чтобы управлять тем, насколько локальной будет регрессия?
  12. Назовите статистические тесты, которые позволяют оценить величину линейного тренда и его значимость.
  13. Назовите статистический тест, который позволяет определить номер члена временного ряда, который разбивает выборку на 2 максимально различающиеся по своим моментами подвыборки?
  14. Какие функции пакета gganimate позволяют осуществлять переходы по времени и состояниям?
  15. Как можно созданную анимацию экспортировать в файл? Какую функцию необходимо вызвать и какие ее пераметры определить для этого?

8.10.2 Упражнения

  1. Загрузите файл с данными по межгодичным изменениям стока на реке Мезень (пост Малонисогорская). Проанализируйте величину и значимость тренда, а также наличие переломного года для характеристик Wpol2 (объем половодья без грунтовой составляющей), а также Wy (суммарный сток). Постройте графики этих характеристик с кривой локальной регрессии. Что можно сказать об их соотношении с грунтовым стоком?

  2. Загрузите файл с данными по суточным расходам на реке Протва (пост Спас-Загорье) и проанализируйте полноту временного ряда. Выполните заполнение пропусков дат и расходов, если это требуется.

  3. Загрузите из сервиса NASA POWER данные по температурам в любой указанной точке с месячной (monthly) дискретностью за последние 50 лет. Используя модель ARIMA, постройте прогноз на последующие 10 лет.

  4. Повторите эксперимент с построением анимационных графиков функции плотности распределения температуры и диаграмм размаха по данным NASA POWER, но выбрав координаты трех других географических локаций.

Самсонов Т.Е. Визуализация и анализ географических данных на языке R. М.: Географический факультет МГУ, 2023. DOI: 10.5281/zenodo.901911