10  Основы картографии

10.1 Предварительные требования

Необходимые для работы пакеты:

library(sf)
library(stars)
library(dplyr)
library(ggplot2)
library(ggrepel)
library(ggnewscale)
library(rnaturalearth)
library(rmapshaper)
library(RColorBrewer)
library(ggspatial)

10.2 Введение

В настоящей главе рассматриваются общие принципы автоматизированного построения карт. Картографическая визуализация базируется на комплексе аспектов, таких как:

• содержание карты;
• охват и масштаб/размер карты;
• картографическая основа;
• генерализация;
• проекция;
• градусная сетка;
• оформление данных;
• легенда;
• компоновка.

При этом многие компоненты неразрывно связаны друг с другом. Например, картографическая основа должна обладать оптимальной детализацией. То есть не быть излишне подробной или, наоборот, генерализованной для выбранного масштаба картографирования. Проекция, в свою очередь, влияет не величину масштаба при фиксированном размере карты, а легенда должны отражать выбранное содержание карты.

В настоящей теме кратко рассмотрены все перечисленные аспекты. В качестве библиотеки для визуализации используется ggplot2. Как и в случае с построением обычных графиков, использование данной библиотеки позволяет достичь гораздо лучшего по сравнению с базовой графикой R контроля над внешним видом изображения. Что позволяет в свою очередь достичь выского качества карт.

10.3 Данные Natural Earth

В качестве источника открытых данных мы будем использовать Natural Earth и WorldClim.

Natural Earth — это открытые мелкомасштабные картографические данные высокого качества. Данные доступны для трех масштабов: 1:10М, 1:50М и 1:110М. Для доступа к этим данным из среды R без загрузки исходных файлов можно использовать пакет rnaturalearth. Пакет позволяет выгружать данные из внешнего репозитория, а также содержит три предзакачанных слоя:

• ne_countries() границы стран
• ne_states() границы единиц АТД 1 порядка
• ne_coastline() береговая линия

Для загрузки других слоев необходимо использовать функцию ne_download(), передав ей масштаб, название слоя и его категорию. Для начала мы поработаем с данными масштаба 110 млн:

countries = ne_countries(scale = 110, returnclass = 'sf')
coast = ne_coastline(scale = 110, returnclass = 'sf')

ocean = ne_download(scale = 110,
                    type = 'ocean',
                    category = 'physical',
                    returnclass = 'sf')

cities = ne_download(scale = 110,
                     type = 'populated_places',
                     category = 'cultural',
                     returnclass = 'sf')

В то же время, каждый раз выкачивать данные для работы бывает неэффективно. Поэтому вы можете скачать себе полную базу данных Natural Earth в формате GeoPackage (GPKG) по ссылке https://www.naturalearthdata.com/downloads/ и положить ее в любую удобную локацию. В этом случае общение с интернетом в процессе построения карт не потребуется:

ne = '/Volumes/Data/Spatial/Natural Earth/natural_earth_vector.gpkg'
rivers = st_read(ne, 'ne_110m_rivers_lake_centerlines', quiet = T)
lakes = st_read(ne, 'ne_110m_lakes', quiet = T)
land = st_read(ne, 'ne_110m_land', quiet = T)
borders = st_read(ne, 'ne_110m_admin_0_boundary_lines_land', quiet = T)

В дальнейшем нам понадобятся данные другой детализации, поэтому объединим текущие данные в список, соответствующий масштабу 110М. Для этого используем функцию lst из пакета tibble, которая элементам списка дает такие же имена как объединяемым элементам:

lyr110 = lst(ocean, land, coast, countries, 
             rivers, lakes, cities, borders)

10.4 Визуализация средствами ggplot2

Пространственные данные поддерживаются в графической подсистеме ggplot2. Для этого существует несколько специализированных функций:

• geom_sf() вызывает stat_sf() и coord_sf() чтобы отобразить объекты типа sf в нужной системе координат;
• geom_stars() отображает объекты типа stars;
• coord_sf() обеспечивает поддержку картографических проекций и позволяет отображать данные в нужной системе координат на лету;
• stat_sf() отвечает за отображение переменных данных на графические переменные для пространственных данных;
• geom_sf_label() позволяет отображать подписи объектов на плашке;
• geom_sf_text() позволяет размещать подписи объектов без плашки.

Создадим на основе прочитанных данных простую карту мира. Будем конструировать карту последовательно, обсуждая что необходимо в ней поменять, чтобы она стала лучше. Для начала просто покажем страны:

ggplot() +
  geom_sf(data = lyr110$countries) +
  theme_void()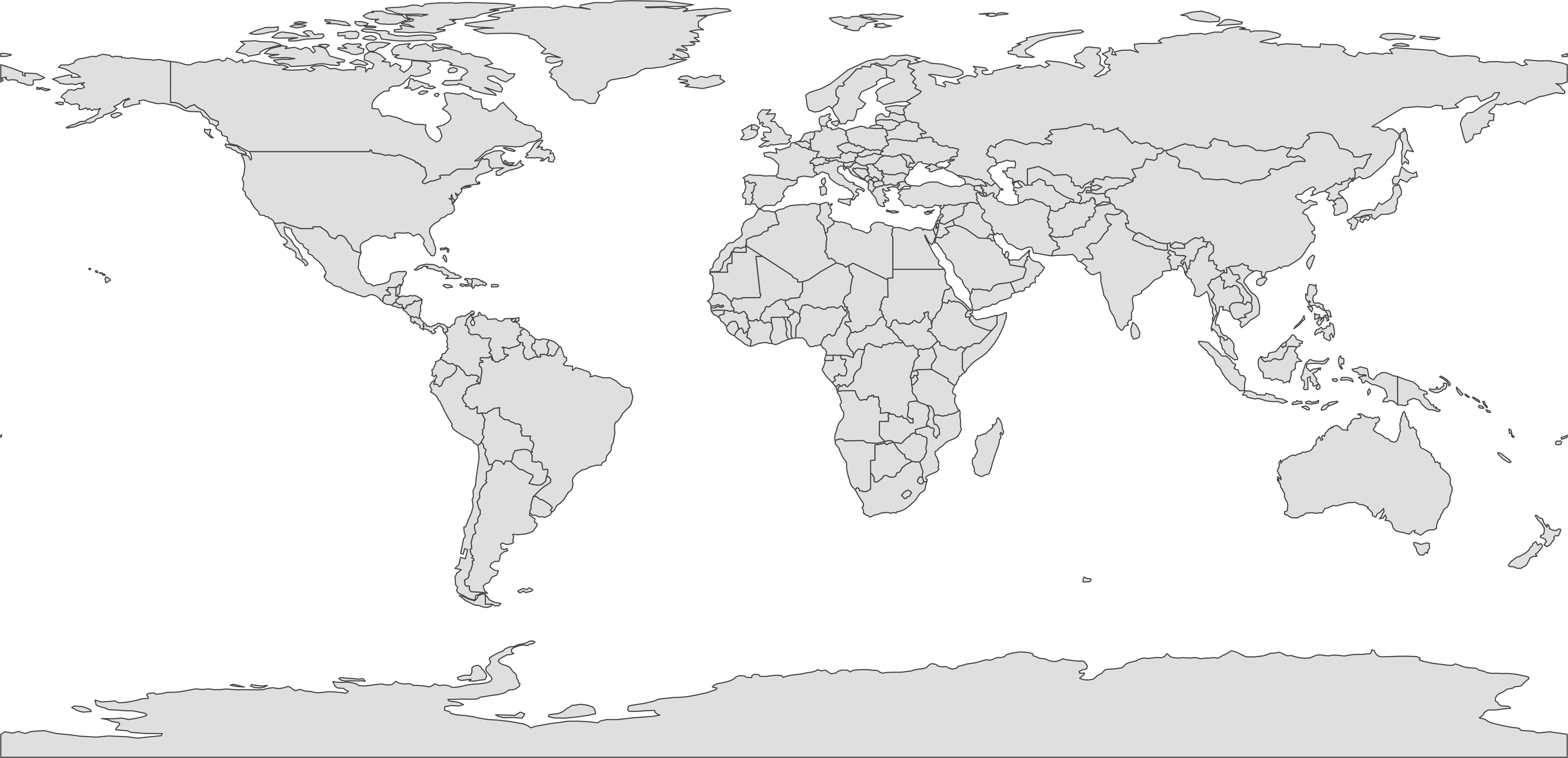

Можно обратить внимание на то, что когда вы отображаете страны полигонами с заливкой, на карте появляются несуществующие границы: на южном полюсе (Антарктида) и вдоль 180-го меридана (на Чукотке). Чтобы такого не происходило, страны всегда визуализируют в 2 слоя: полигонами без обводки и линейными границами поверх:

ggplot() +
  geom_sf(data = lyr110$countries, color = NA) +
  geom_sf(data = lyr110$borders, linewidth = 0.2) +
  theme_void()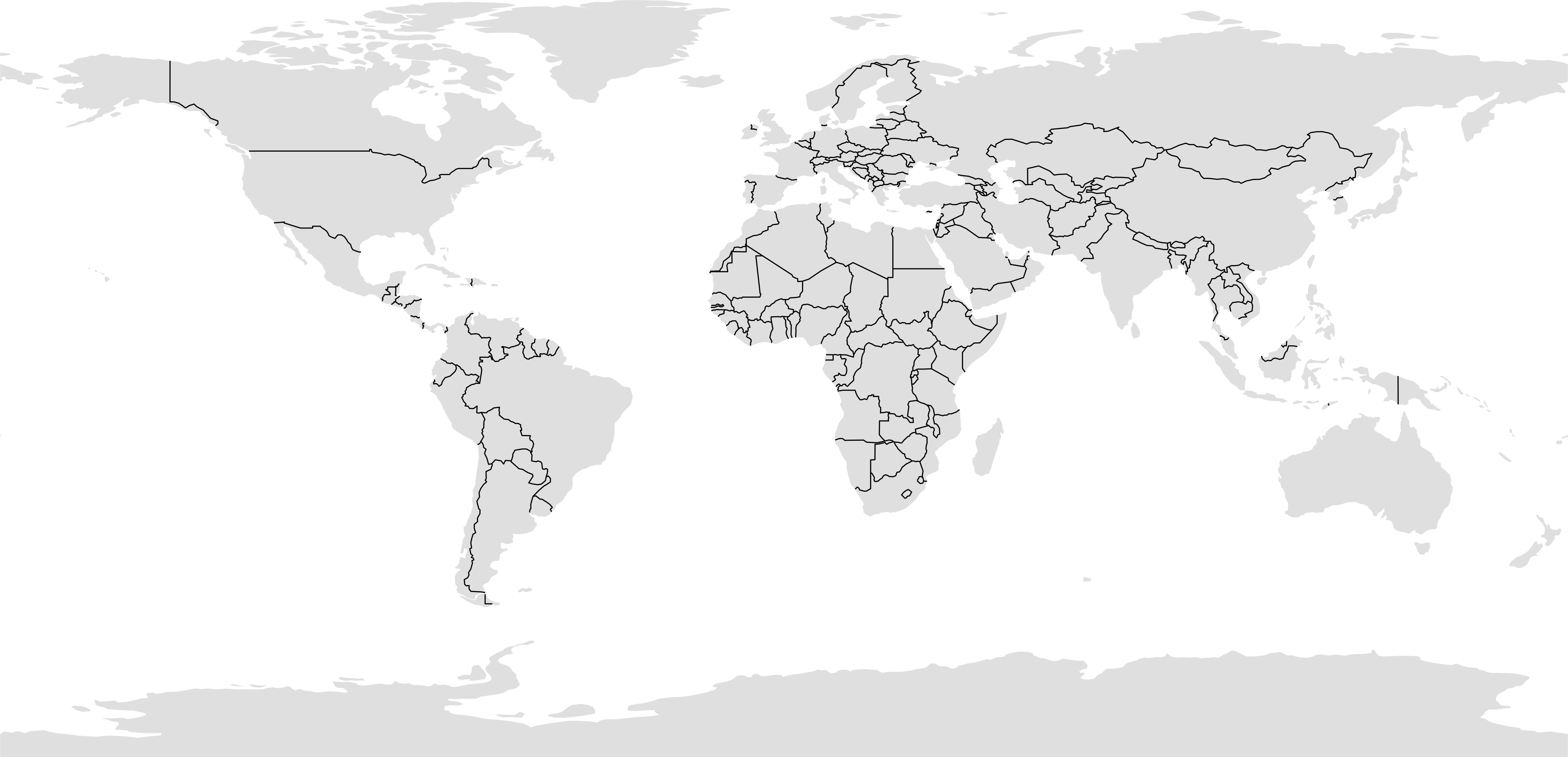

Убрав обводку стран, мы потеряли береговую линию. Будет логично добавить на карту океан. Однако если отобразить его полигоном с обводкой, как мы попытались изначально поступить при визуализации стран, по границе карты возникнут несуществующие береговые линии:

ggplot() +
  geom_sf(data = lyr110$countries, color = NA) +
  geom_sf(data = lyr110$borders, linewidth = 0.2) +
  geom_sf(data = lyr110$ocean, linewidth = 0.4, 
          fill = 'azure', color = 'steelblue') +
  theme_void()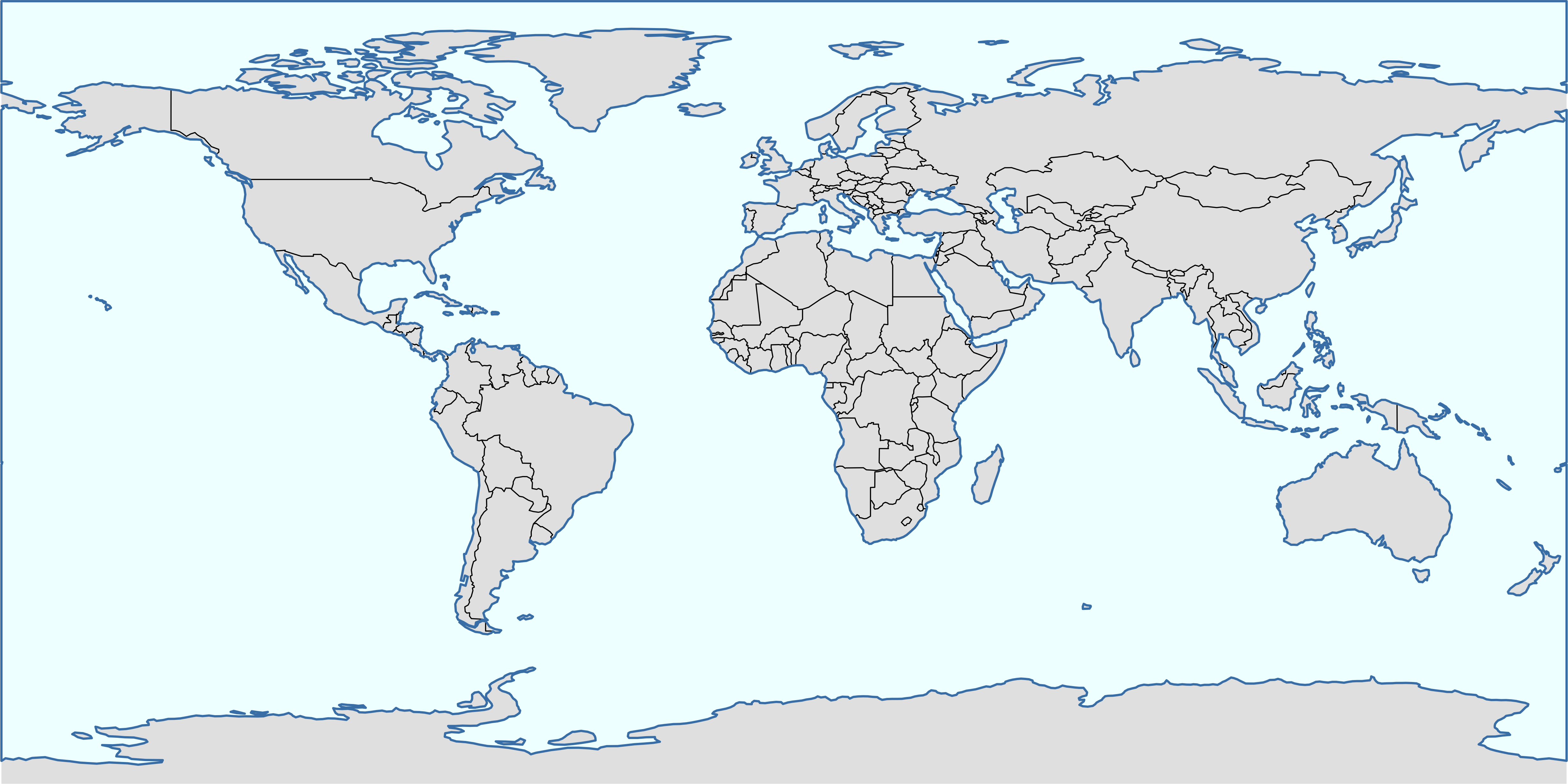

Это означает, что для отображения морских акваторий следует использовать аналогичный прием совмещения полигональных объектов без обводки и их линейной границы:

ggplot() +
  geom_sf(data = lyr110$countries, color = NA) +
  geom_sf(data = lyr110$borders, linewidth = 0.2) +
  geom_sf(data = lyr110$ocean, 
          fill = 'azure', color = NA) +
  geom_sf(data = lyr110$coast, 
          size = 0.4, color = 'steelblue') +
  theme_void()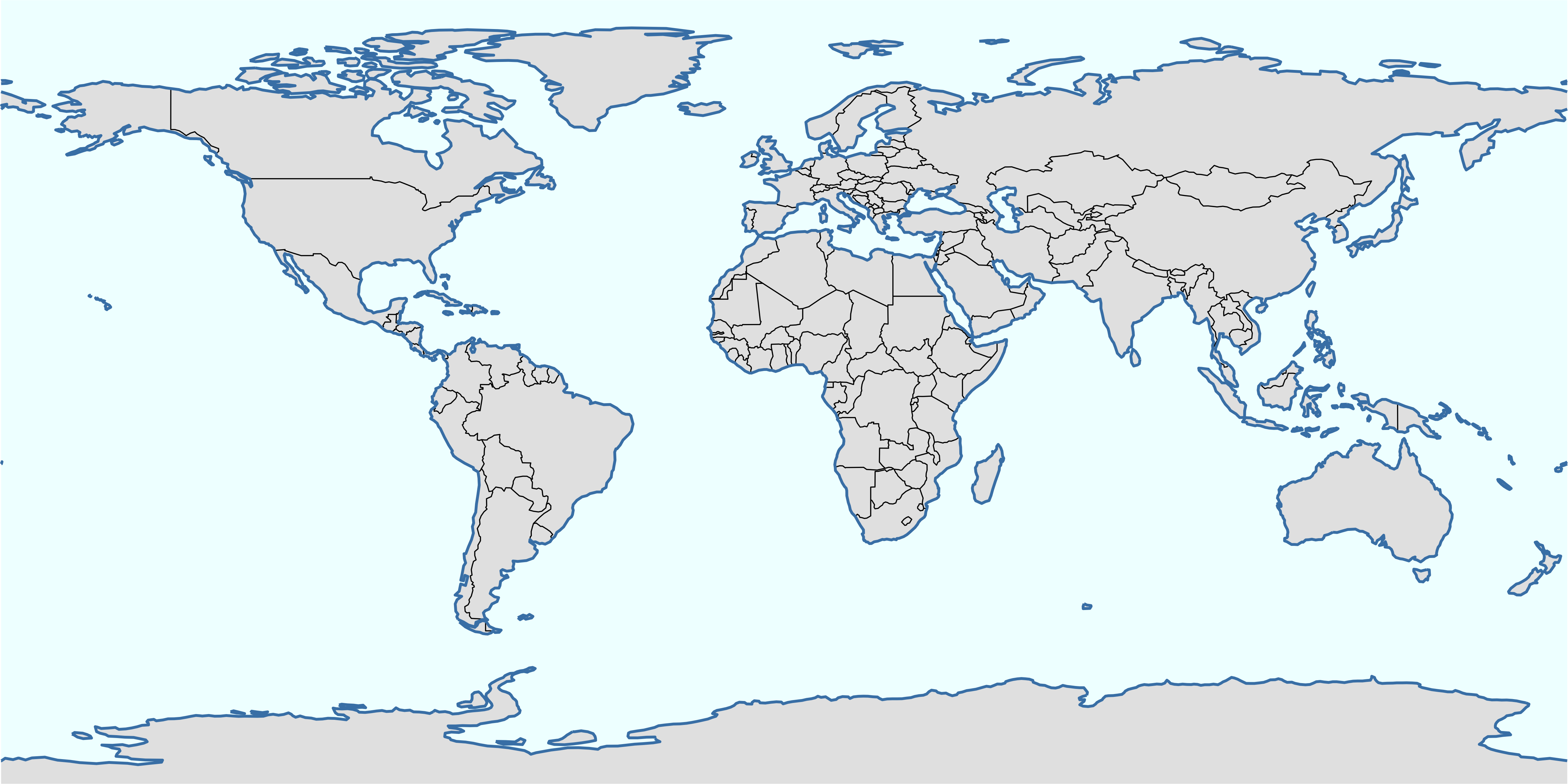

Добавим раскраску стран по их политической принадлежности. При отображении пространственных данных действуют принципы задания графических переменных, аналогичные построению обычных графиков: через mapping = aes(...). Воспользуемся готовым атрибутивным полем в таблице данных для создания политико-административной раскраски:

ggplot() +
  geom_sf(data = lyr110$countries, color = NA, 
          mapping = aes(fill = as.factor(mapcolor7)), show.legend = FALSE) +
  scale_fill_manual(values = brewer.pal(7, 'Set2')) +
  geom_sf(data = lyr110$borders, linewidth = 0.2) +
  geom_sf(data = lyr110$ocean, fill = 'azure', color = NA) +
  geom_sf(data = lyr110$coast, linewidth = 0.4, color = 'steelblue4') +
  theme_void()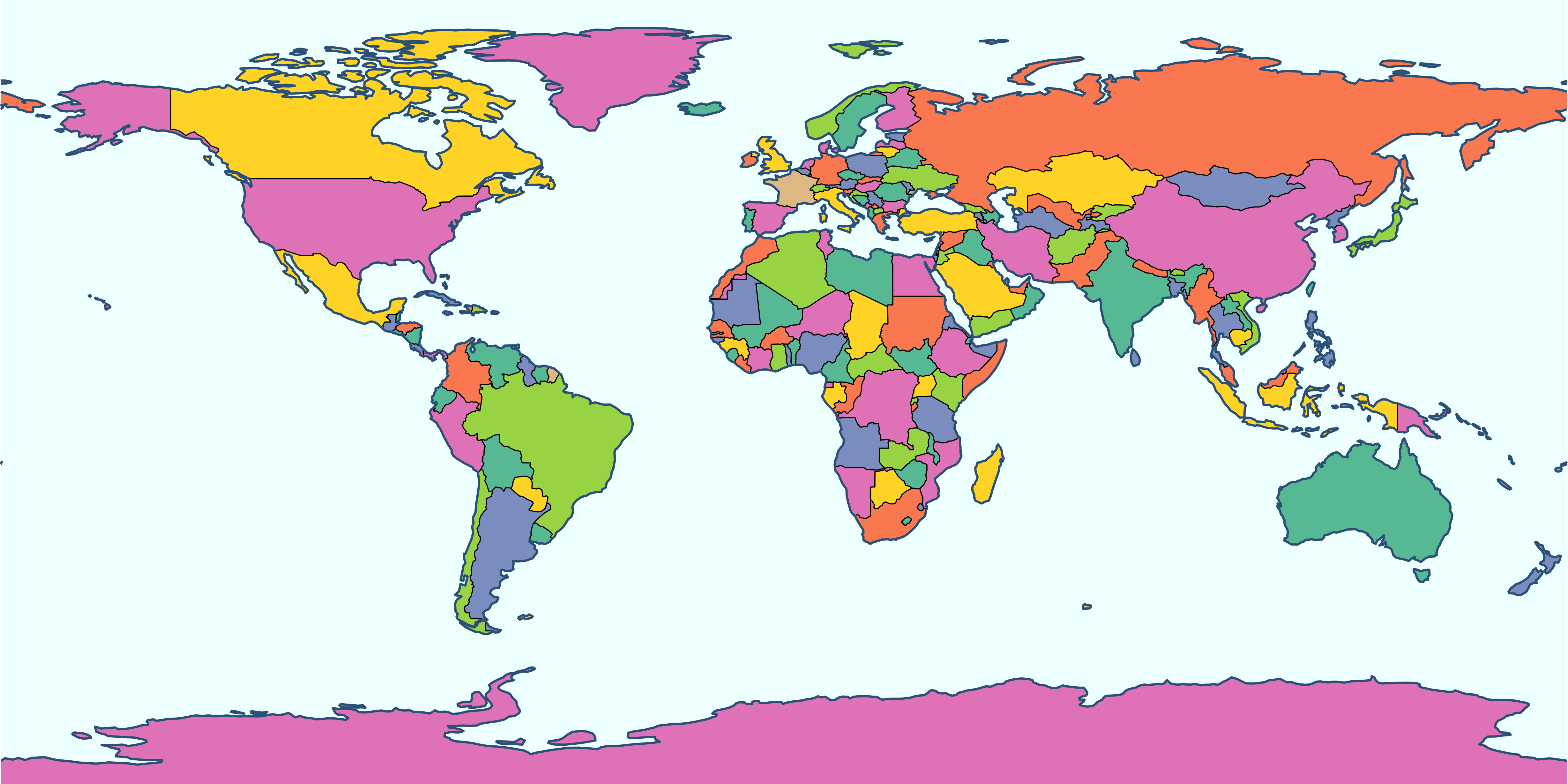

Нанесем на карту точки и подписи крупнейших столиц. Для нанесения подписей используем geom_sf_text() с параметром nudge_y, чтобы сдвинуть подписи вверх относительно пунсонов. Помимо этого, чтобы понизить многословность кода, для дальнейших экспериментов перенесем посторяющиеся слои вы список:

lyr110$megacities = lyr110$cities |> 
  filter(SCALERANK == 0, 
         ! NAME %in% c('Washington, D.C.', 'Paris', 'Riyadh', 'Rome', 'São Paulo', 'Kolkata'))

basemap = list(
  geom_sf(data = lyr110$countries, color = NA, 
          mapping = aes(fill = as.factor(mapcolor7)), show.legend = FALSE),
  scale_fill_manual(values = brewer.pal(7, 'Set2')),
  geom_sf(data = lyr110$borders, linewidth = 0.2),
  geom_sf(data = lyr110$ocean, fill = 'azure', color = NA),
  geom_sf(data = lyr110$coast, linewidth = 0.4, color = 'steelblue4'),
  geom_sf(data = lyr110$megacities, shape = 21, fill = 'white', stroke = 0.75, linewidth = 2)
)

ggplot() +
  basemap +
  geom_sf_text(data = lyr110$megacities, mapping = aes(label = NAME),
               size = 3, nudge_y = 5, family = 'Open Sans', fontface = 'bold') +
  theme_void()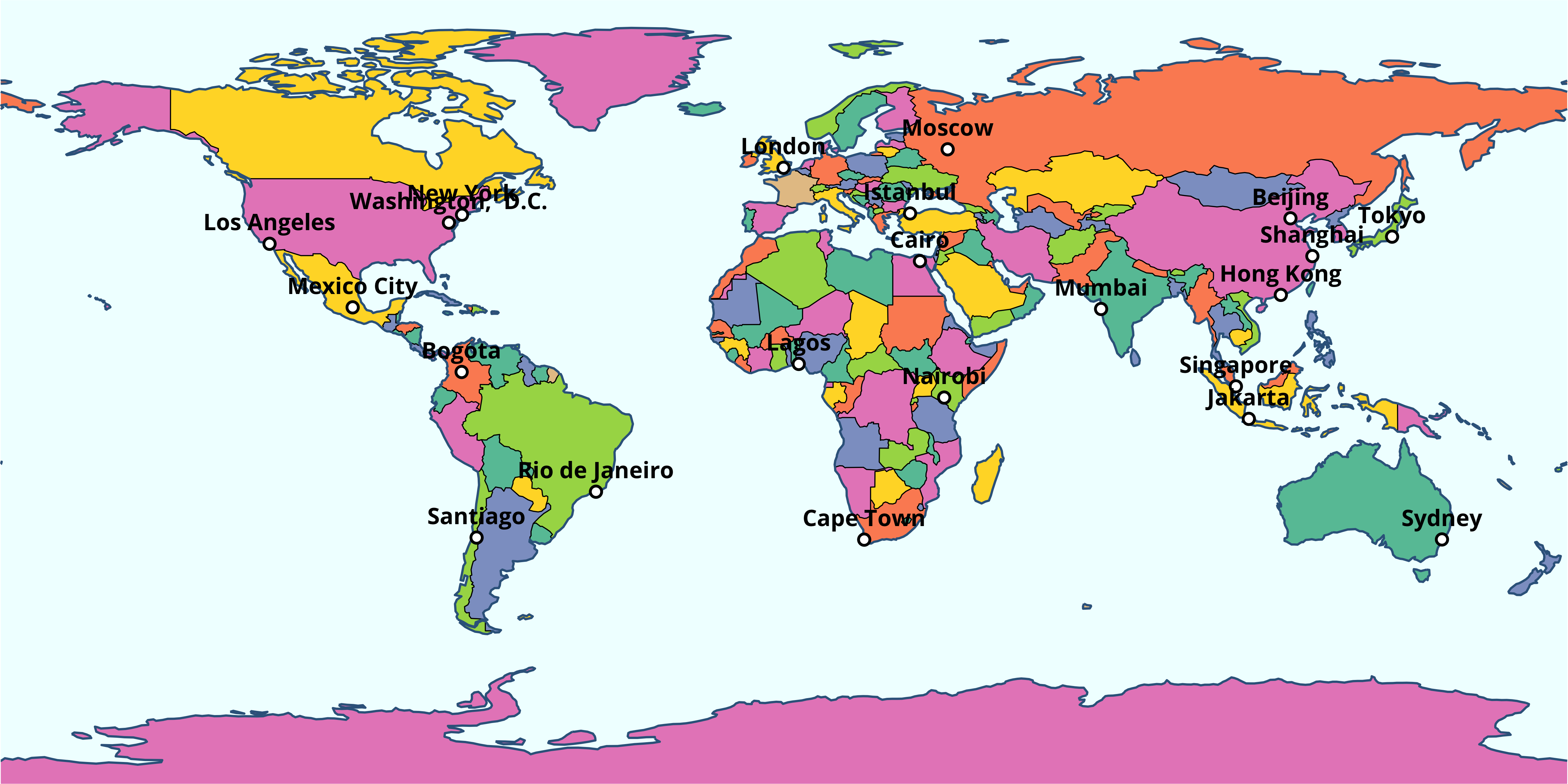

С подписями точечных объектов, однако, более удобно работать с применением пакета ggrepel, который расставляет их автоматически вокруг точек:

ggplot() +
  basemap +
  geom_text_repel(data = lyr110$megacities, stat = "sf_coordinates",
                  size = 3, aes(label = NAME, geometry = geometry), 
                  family = 'Open Sans', fontface = 'bold') +
  theme_void()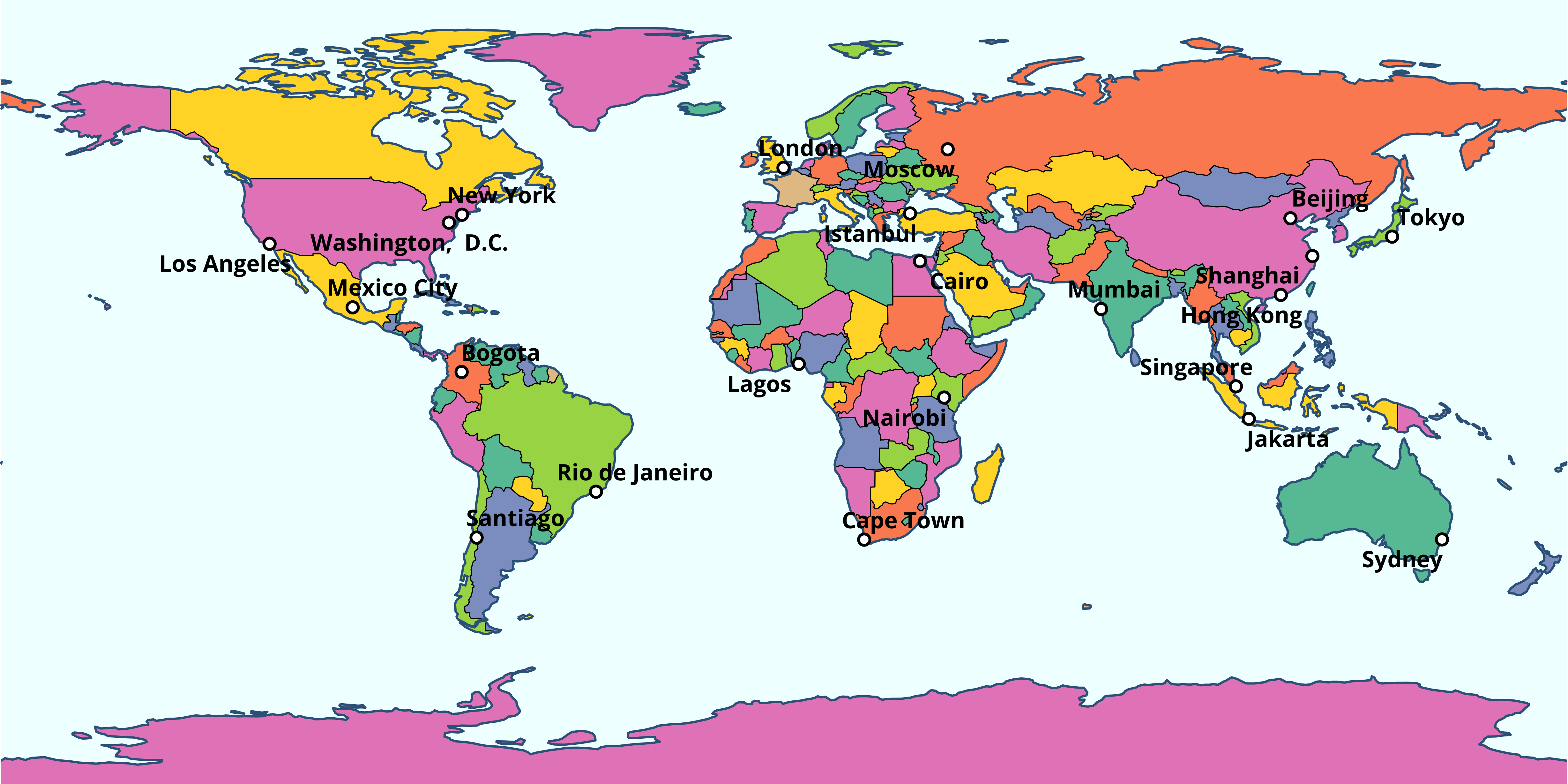

В данном случае все неплохо, но подписи читаются недостаточно хорошо из-за контраста с фоном и береговой линией. Для улучшения читаемости можно сделать заливку стран менее насыщенной, увеличив прозрачность. При этом надо и обводку для точек сделать менее контрастной, чтобы она не выделялась на фоне стран — все-таки, на общегеографических и политико-административных картах равнозначны:

basemap0 = list(
  geom_sf(data = lyr110$countries, color = NA, 
          alpha = 0.5,
          mapping = aes(fill = as.factor(mapcolor7)), show.legend = FALSE),
  scale_fill_manual(values = brewer.pal(7, 'Set2')),
  geom_sf(data = lyr110$borders, alpha = 0.5, linewidth = 0.2),
  geom_sf(data = lyr110$ocean, fill = 'azure', color = NA),
  geom_sf(data = lyr110$coast, alpha = 0.5, linewidth = 0.4, color = 'steelblue4'),
  geom_sf(data = lyr110$megacities, shape = 21, fill = 'white', stroke = 0.75, linewidth = 2)
)

ggplot() +
  basemap0 +
  geom_text_repel(data = lyr110$megacities, stat = "sf_coordinates",
                  size = 3, aes(label = NAME, geometry = geometry), 
                  family = 'Open Sans', fontface = 'bold') +
  theme_void()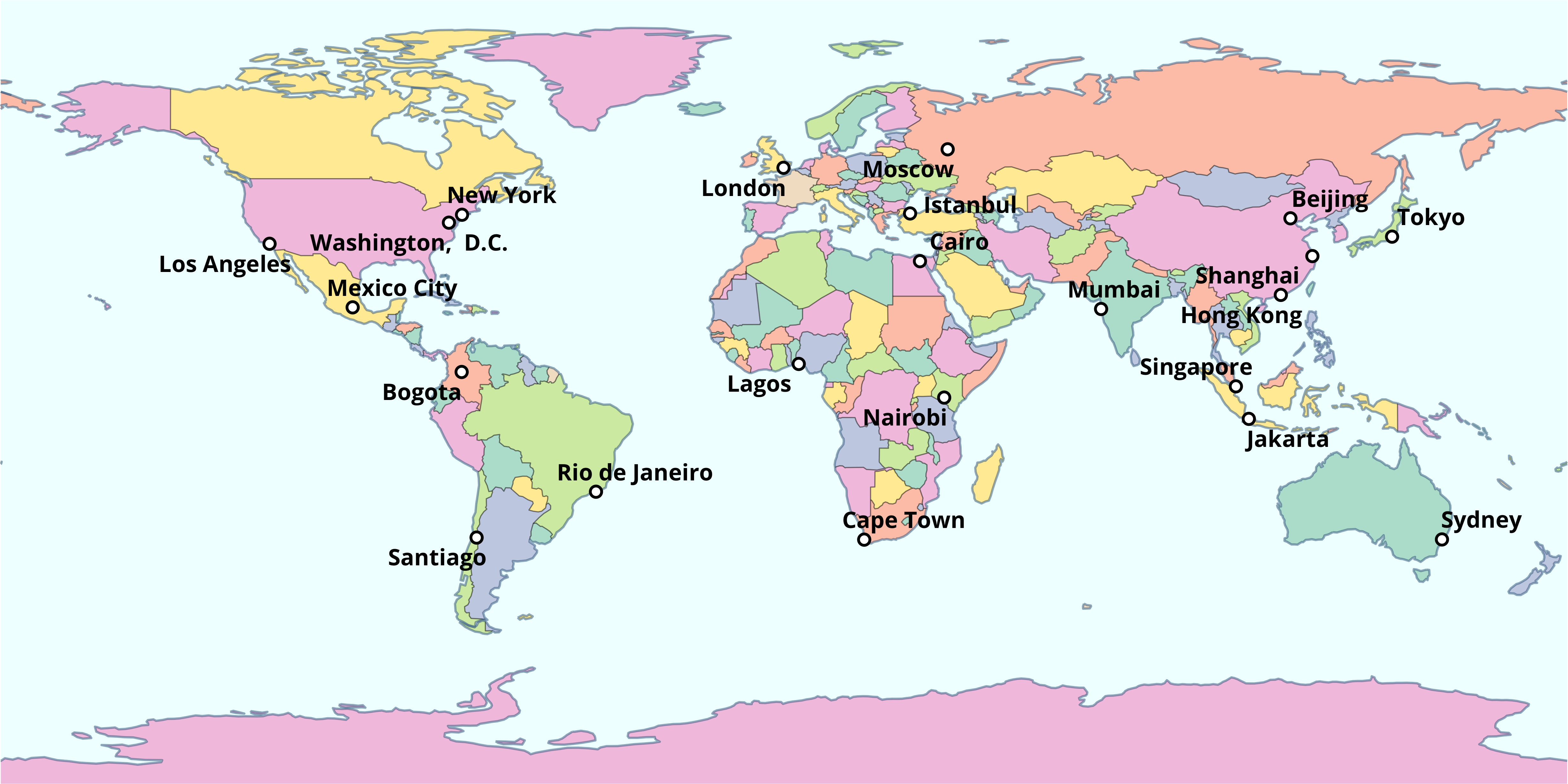

В качестве альтернативного решения можно добавить лекий полупрозрачный фон под подписями городов. Для этого нужно изменить геометрию с geom_text_repel на geom_label_repel и определить цвет заливки фона:

ggplot() +
  basemap +
  geom_label_repel(data = lyr110$megacities, stat = "sf_coordinates",
                  aes(label = NAME, geometry = geometry), 
                  size = 3, 
                  label.size = NA, 
                  label.padding=.1, 
                  fill = alpha("white", 0.7), 
                  family = 'Open Sans', fontface = 'bold') +
  theme_void()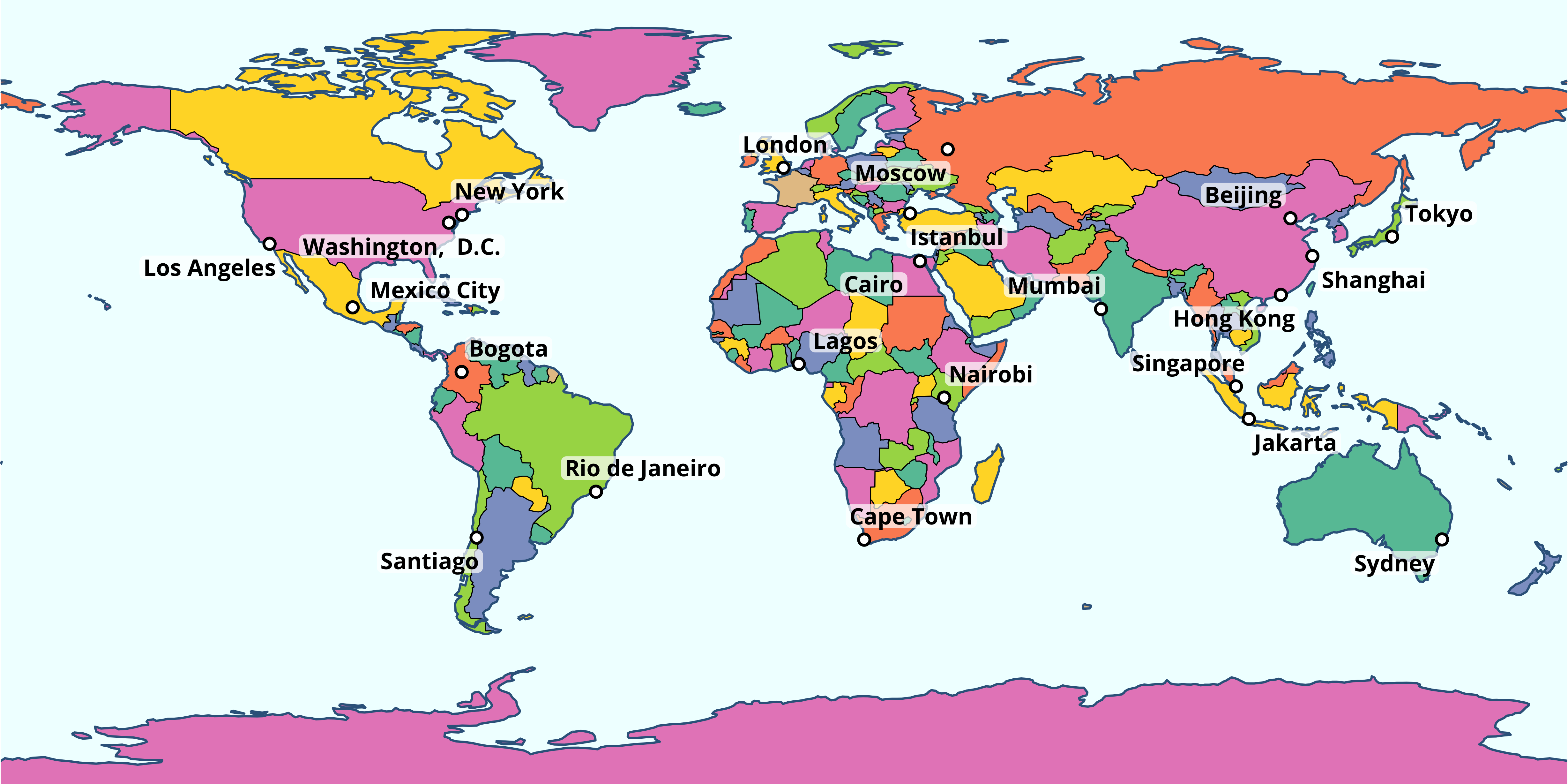

10.5 Проекции и градусные сетки

Когда вы отображаете данные в градусах, не определяя проекцию, они визуализируются в цилиндрической равнопромежуточной проекции. Такая проекция не очень удобна для визуализации земного шара. Запишем исходную карту без проекции в отдельную переменную и визуализируем ее с помощью разных проекций:

map = ggplot() +
  geom_sf(data = lyr110$countries, color = NA,
          mapping = aes(fill = as.factor(mapcolor7)), show.legend = FALSE) +
  scale_fill_manual(values = brewer.pal(7, 'Set2')) +
  geom_sf(data = lyr110$borders, linewidth = 0.2) +
  geom_sf(data = lyr110$ocean, fill = 'azure', color = NA) +
  geom_sf(data = st_wrap_dateline(lyr110$coast), linewidth = 0.4, color = 'steelblue4') +
  geom_sf(data = lyr110$megacities, shape = 21, fill = 'white', stroke = 0.75, size = 2) +
  geom_label_repel(
    data = lyr110$megacities, stat = "sf_coordinates",
    aes(label = NAME, geometry = geometry),
    size = 3,
    label.size = NA,
    label.padding=.1,
    fill = alpha("white", 0.7),
    family = 'Open Sans', fontface = 'bold'
  ) +
  labs(x = NULL, y = NULL) +
  theme_minimal()

map + coord_sf(crs = "+proj=moll")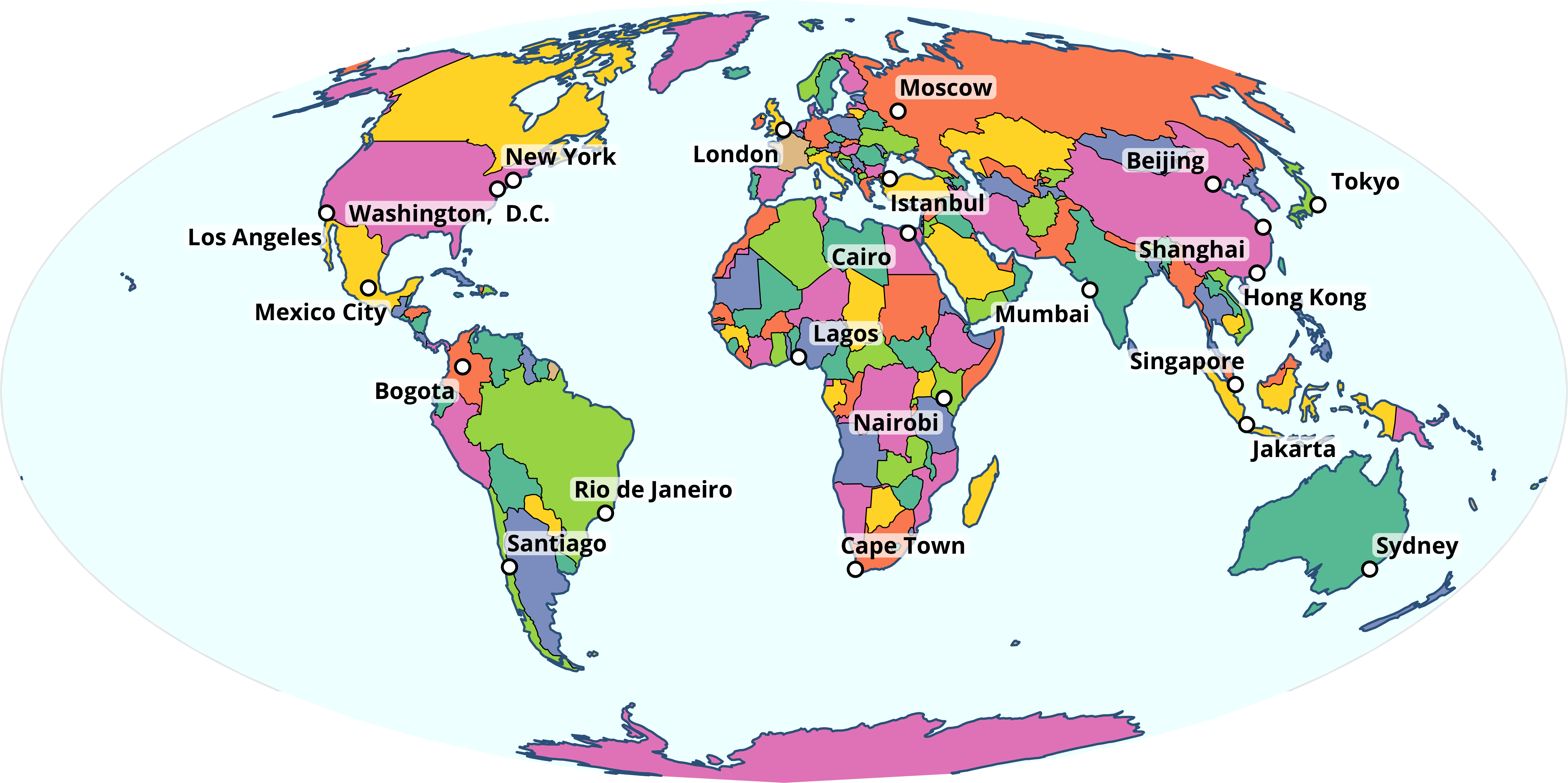

map + coord_sf(crs = "+proj=eck3")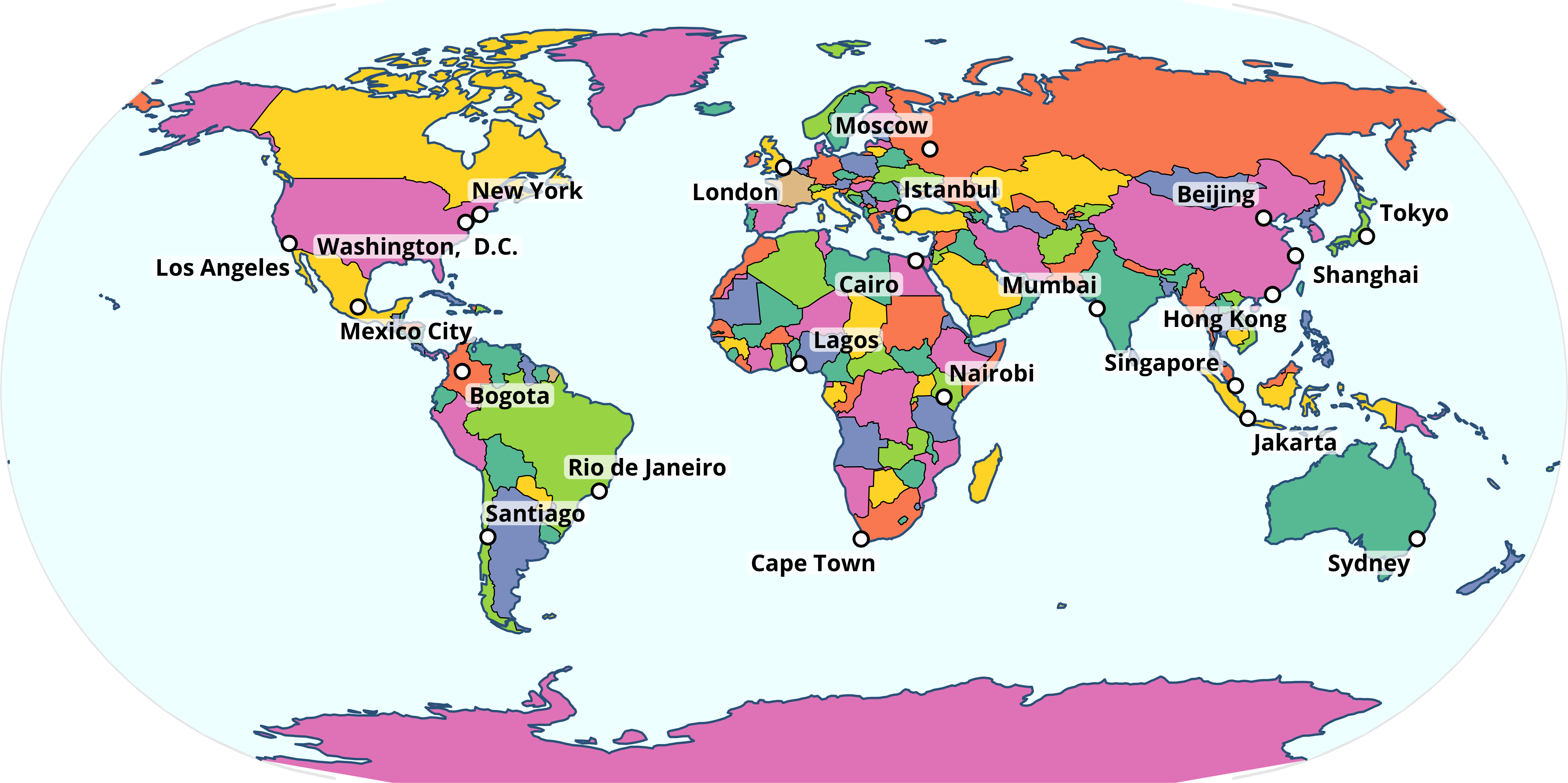

map + coord_sf(crs = "+proj=eqearth")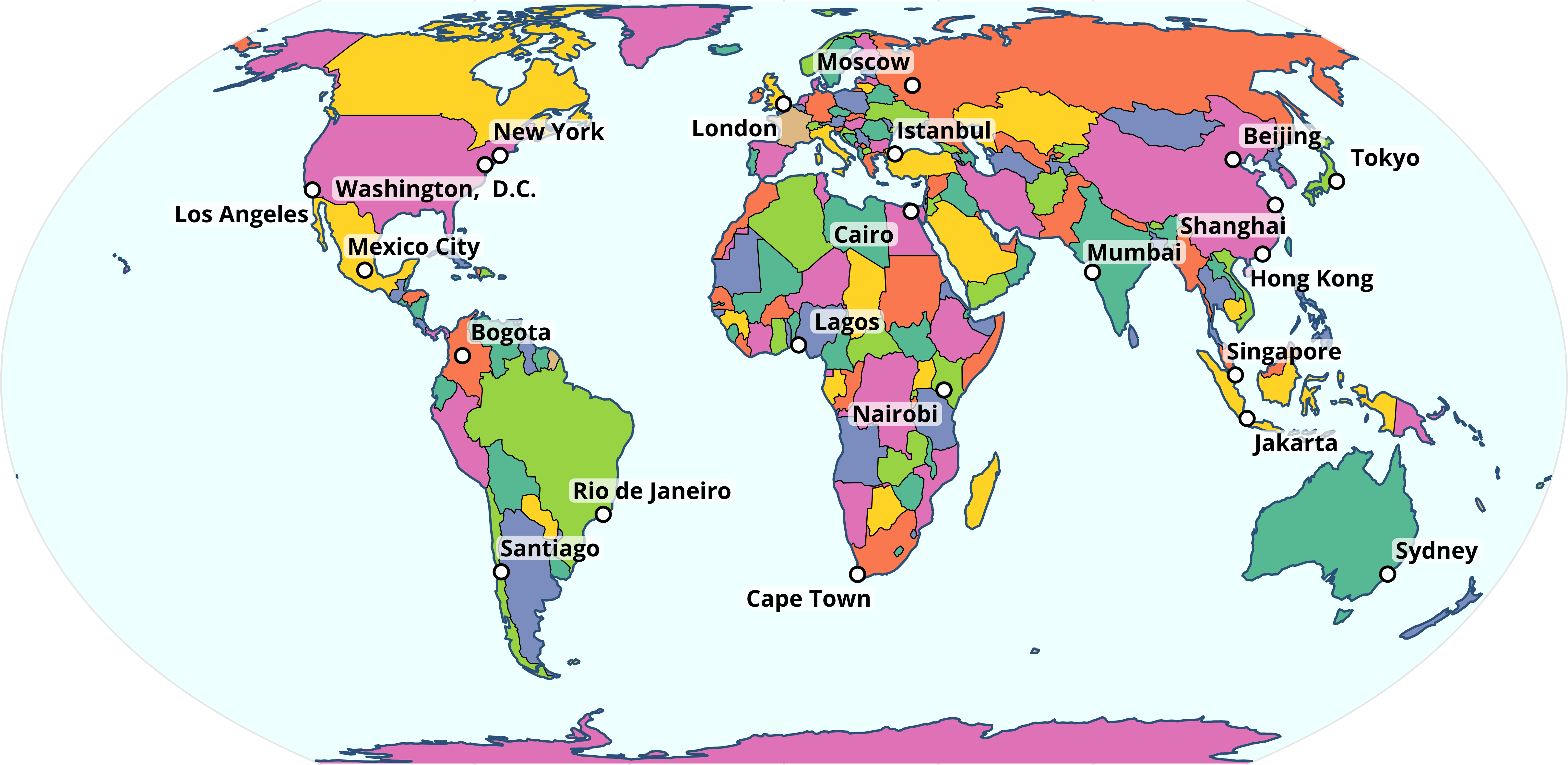

map + coord_sf(crs = "+proj=times")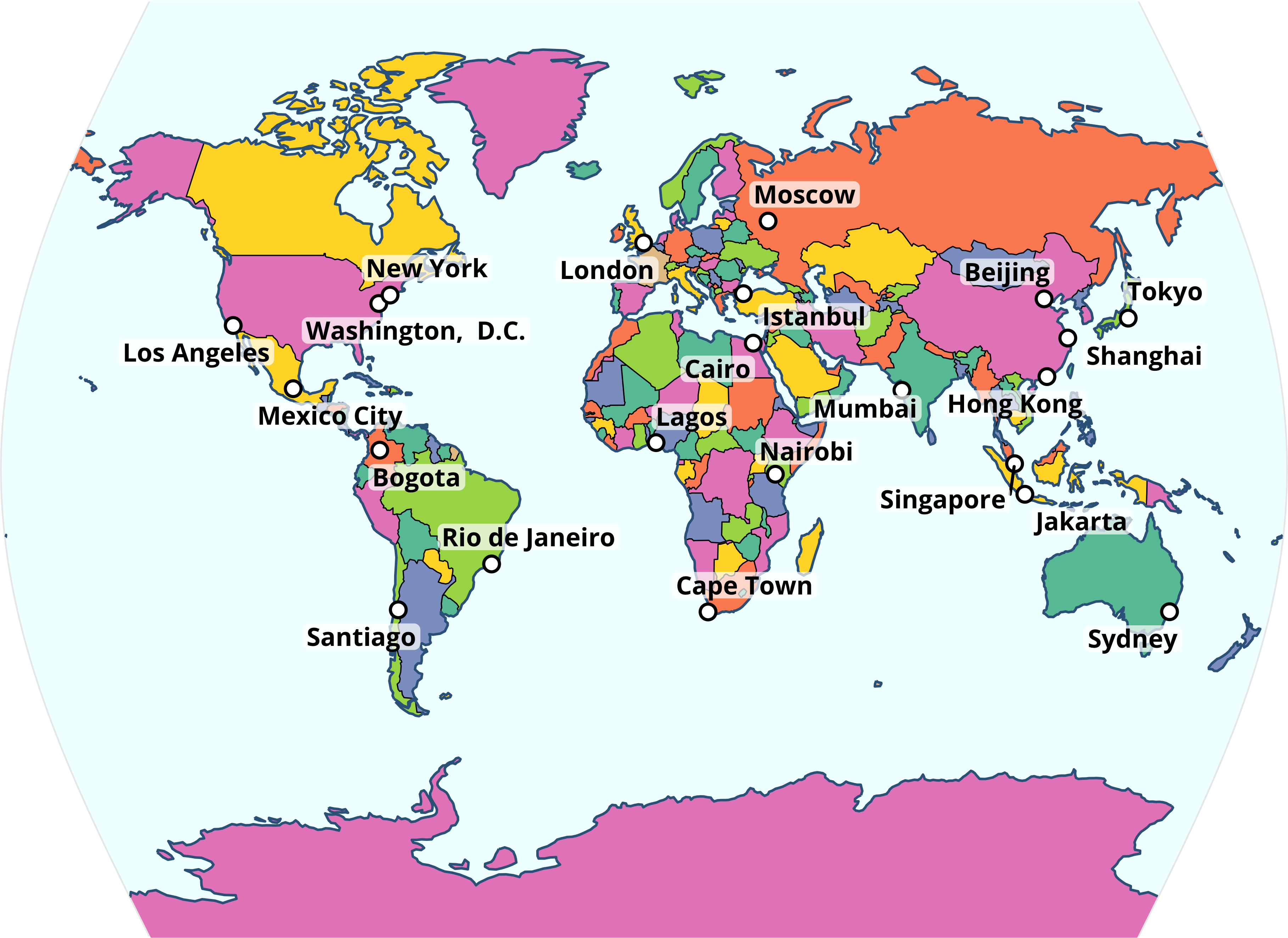

map + coord_sf(crs = "+proj=mill")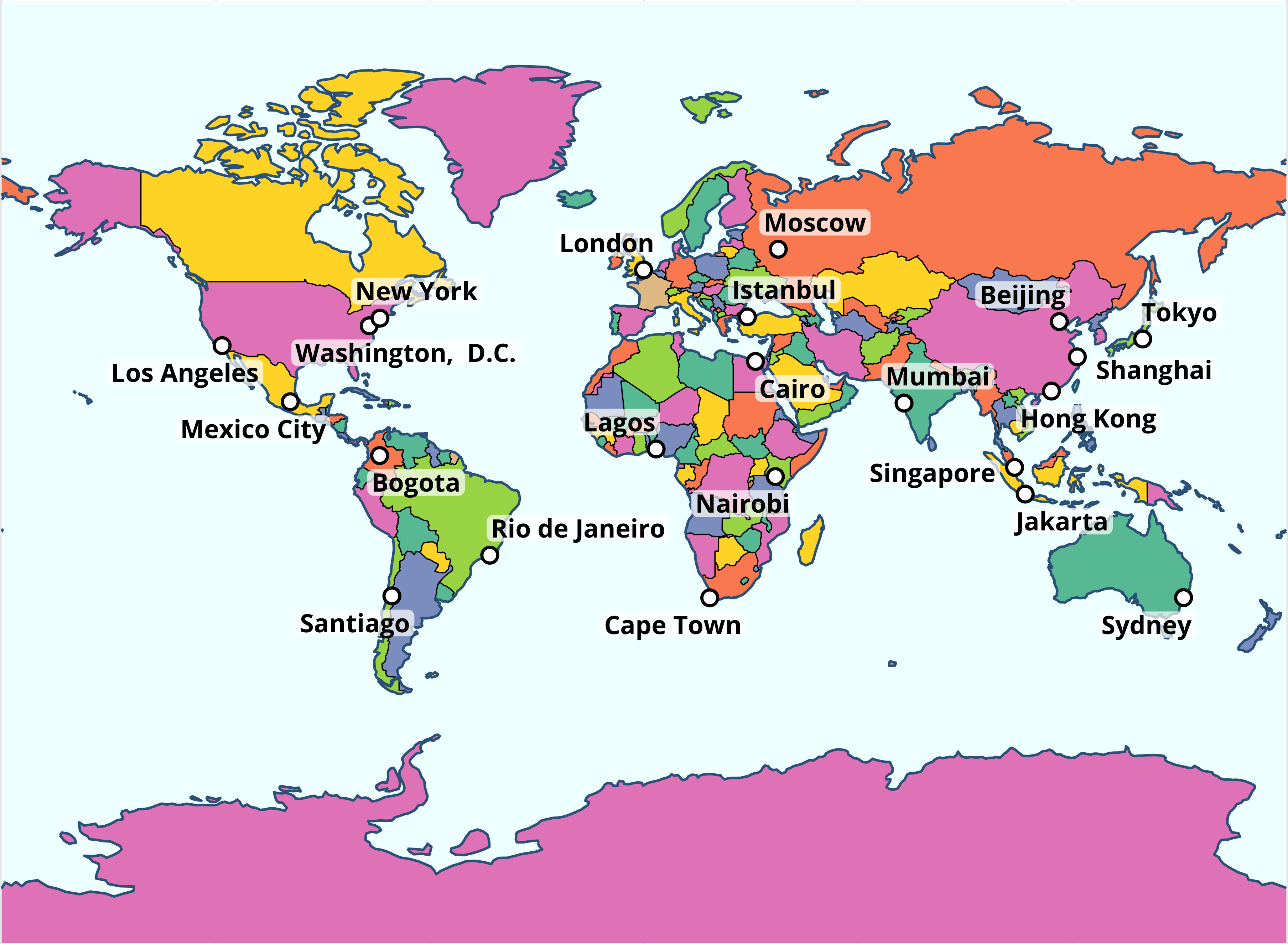

Добавим теперь линии градусной сетки:

lons = seq(-180, 180, by = 30)
lats = seq(-90, 90, by = 30)

grat = st_graticule(lon = lons, lat = lats)

box = st_bbox(c(xmin = -180, xmax = 180, 
                ymax = 90,   ymin = -90), 
              crs = st_crs(4326)) |> 
  st_as_sfc() |> 
  smoothr::densify(max_distance = 1) 

degree_labels = function(grat, vjust, hjust, size, lon = T, lat = T) {
  pts = grat |>  
    st_cast('POINT') |> 
    group_by(degree, type, degree_label) |> 
    filter(row_number() == 1)
    
  list(
    if (lon) geom_sf_text(data = filter(pts, type == 'E'), vjust = vjust, size = size,
                 mapping = aes(label = degree_label), parse = TRUE),
    if (lat) geom_sf_text(data = filter(pts, type == 'N'), hjust = hjust, size = size,
                 mapping = aes(label = degree_label), parse = TRUE)
  )  
}

map + 
  geom_sf(data = grat, linewidth = 0.1) +
  geom_sf(data = box, linewidth = 0.5, fill = NA) +
  coord_sf(crs = "+proj=moll") +
  degree_labels(grat, vjust = +1.5, hjust = +1.5, size = 3, lon = F)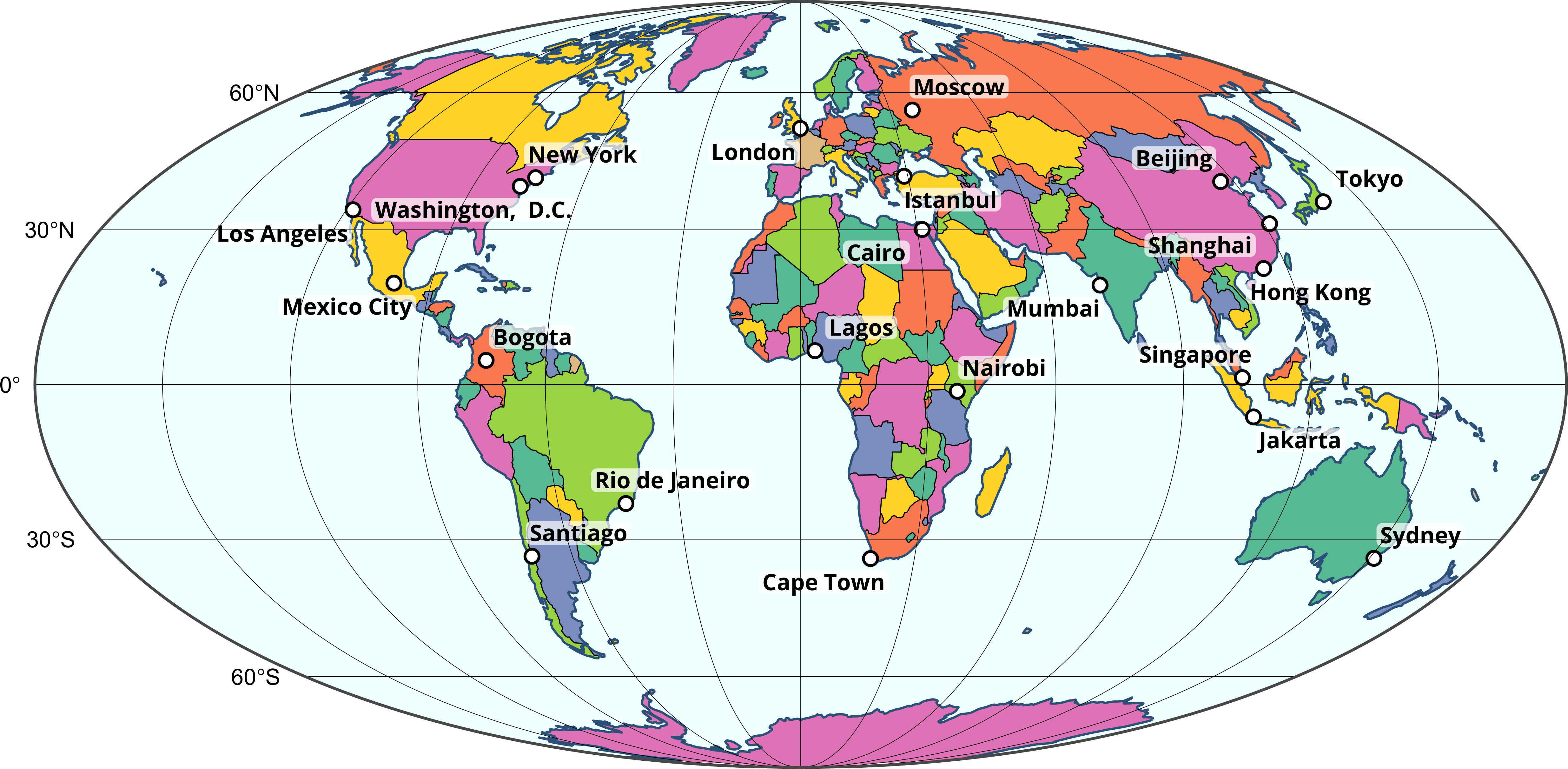

map + 
  geom_sf(data = grat, linewidth = 0.1) +
  geom_sf(data = box, linewidth = 0.5, fill = NA) +
  coord_sf(crs = "+proj=eck3") +
  degree_labels(grat, vjust = +1.5, hjust = +1.5, size = 3)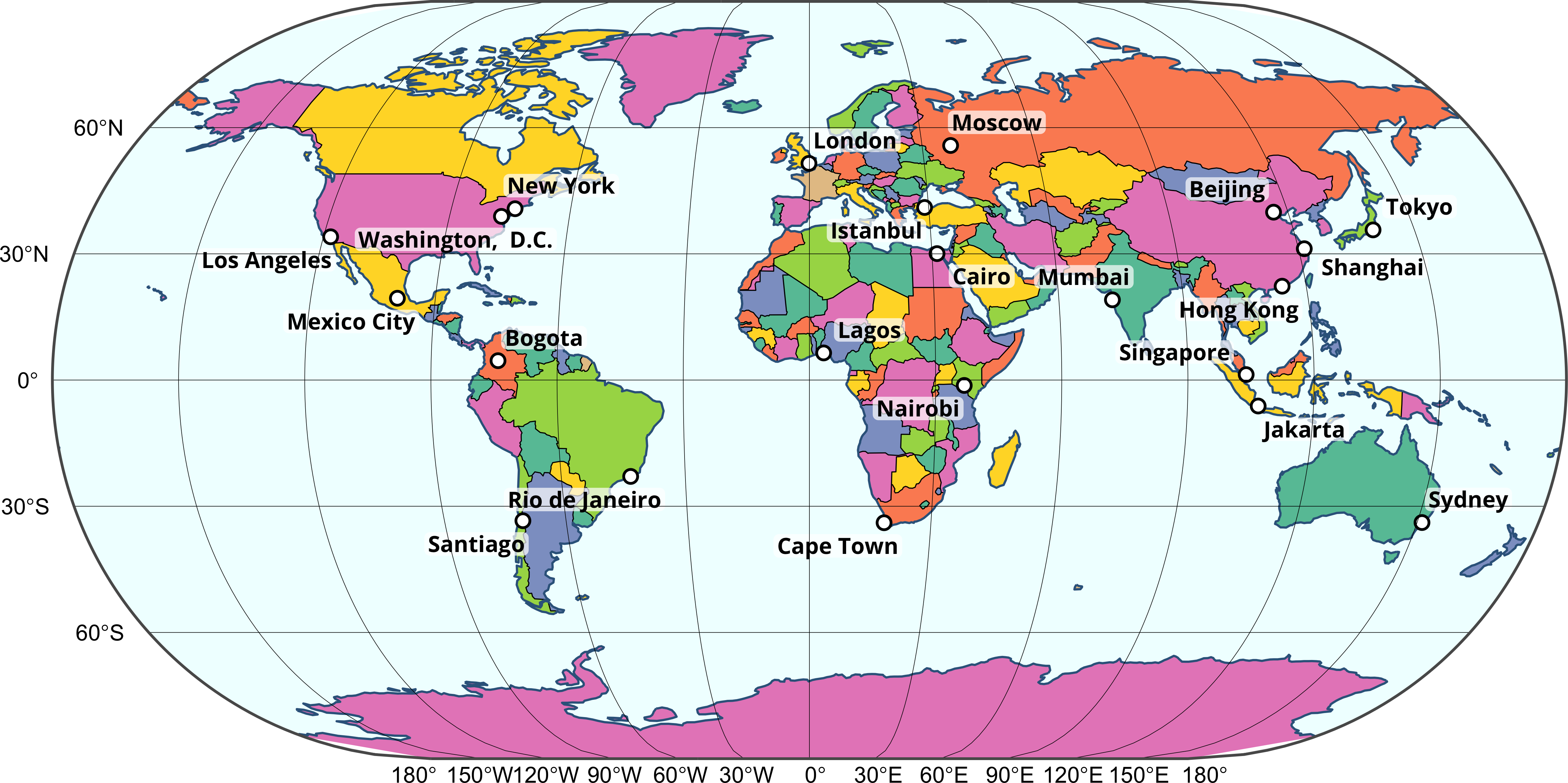

map + 
  geom_sf(data = grat, linewidth = 0.1) +
  geom_sf(data = box, linewidth = 0.5, fill = NA) +
  coord_sf(crs = "+proj=eqearth") +
  degree_labels(grat, vjust = +1.5, hjust = +1.5, size = 3)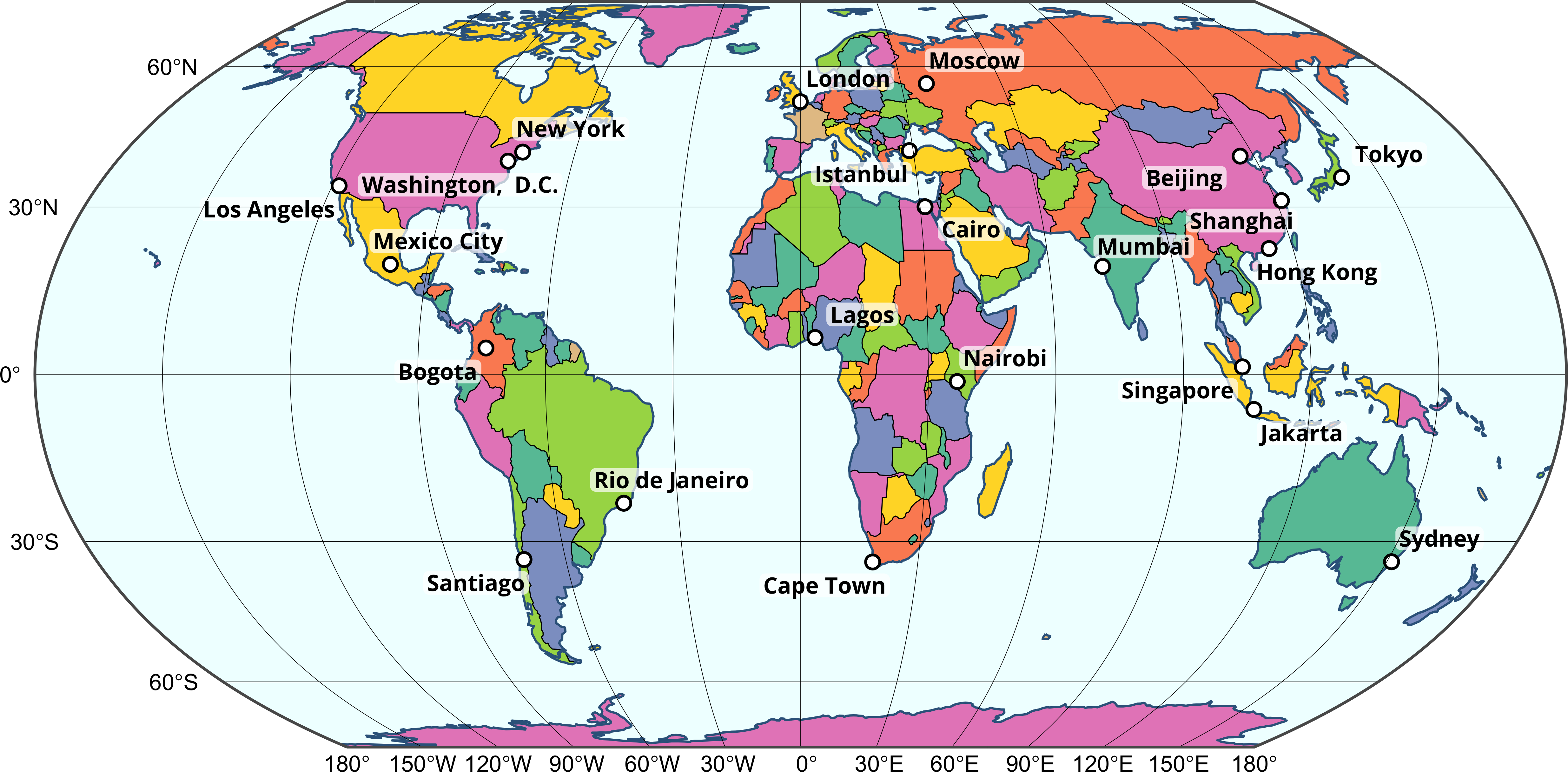

map + 
  geom_sf(data = grat, linewidth = 0.1) +
  geom_sf(data = box, linewidth = 0.5, fill = NA) +
  coord_sf(crs = "+proj=times") +
  degree_labels(grat, vjust = +1.5, hjust = +1.5, size = 3)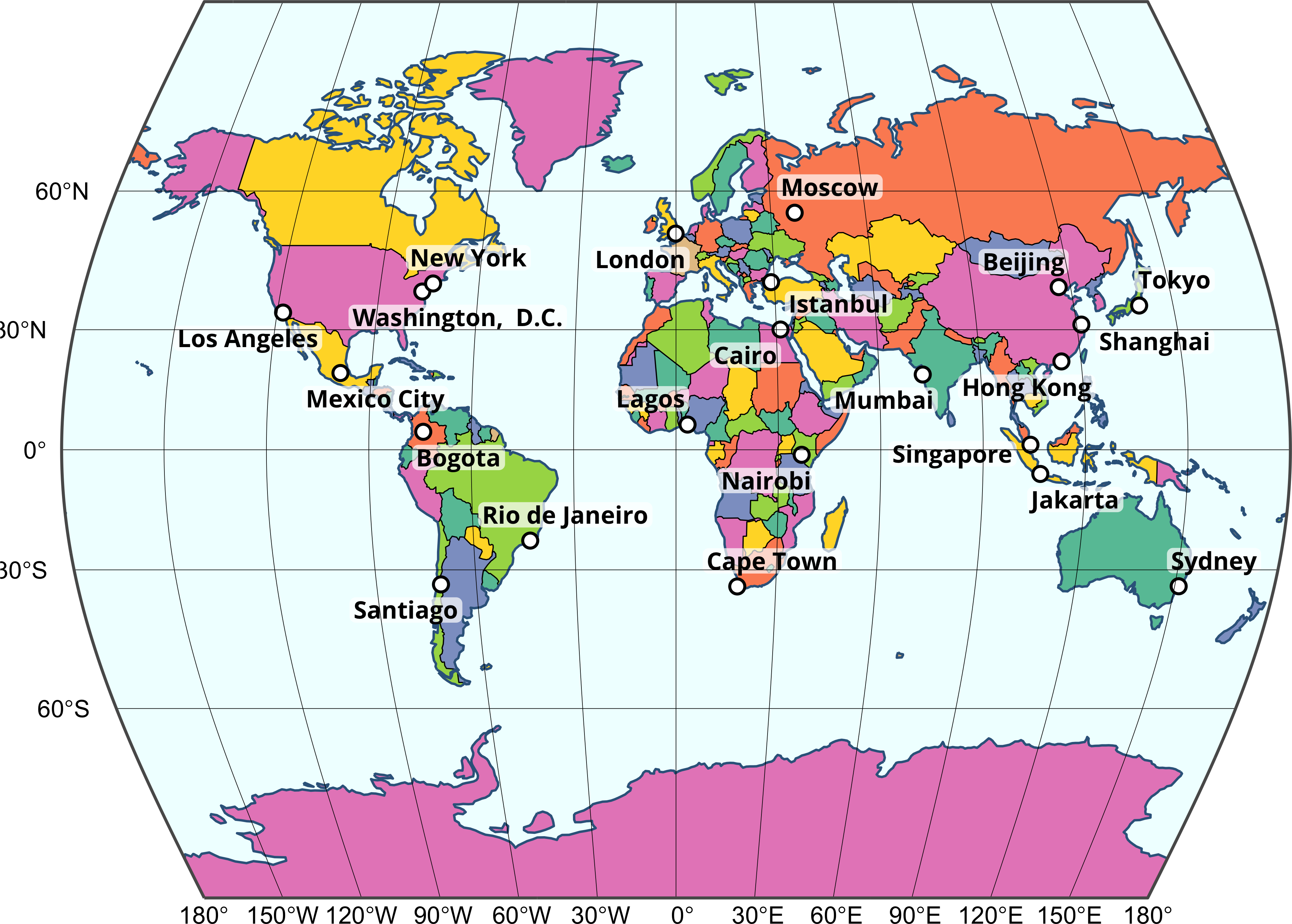

10.5.1 Отображение растровых данных

На общегеографических картах довольно часто присутствует изображение рельефа. Чтобы добавить его на карту, можно использовать специальный тип геометрии geom_stars:

dem = read_stars('data/world/gebco.tif') # Цифровая модель рельефа

ggplot() +
  geom_stars(data = dem) +
  geom_sf(data = lyr110$coast, linewidth = 0.4, color = 'white') +
  coord_sf() +
  theme_void()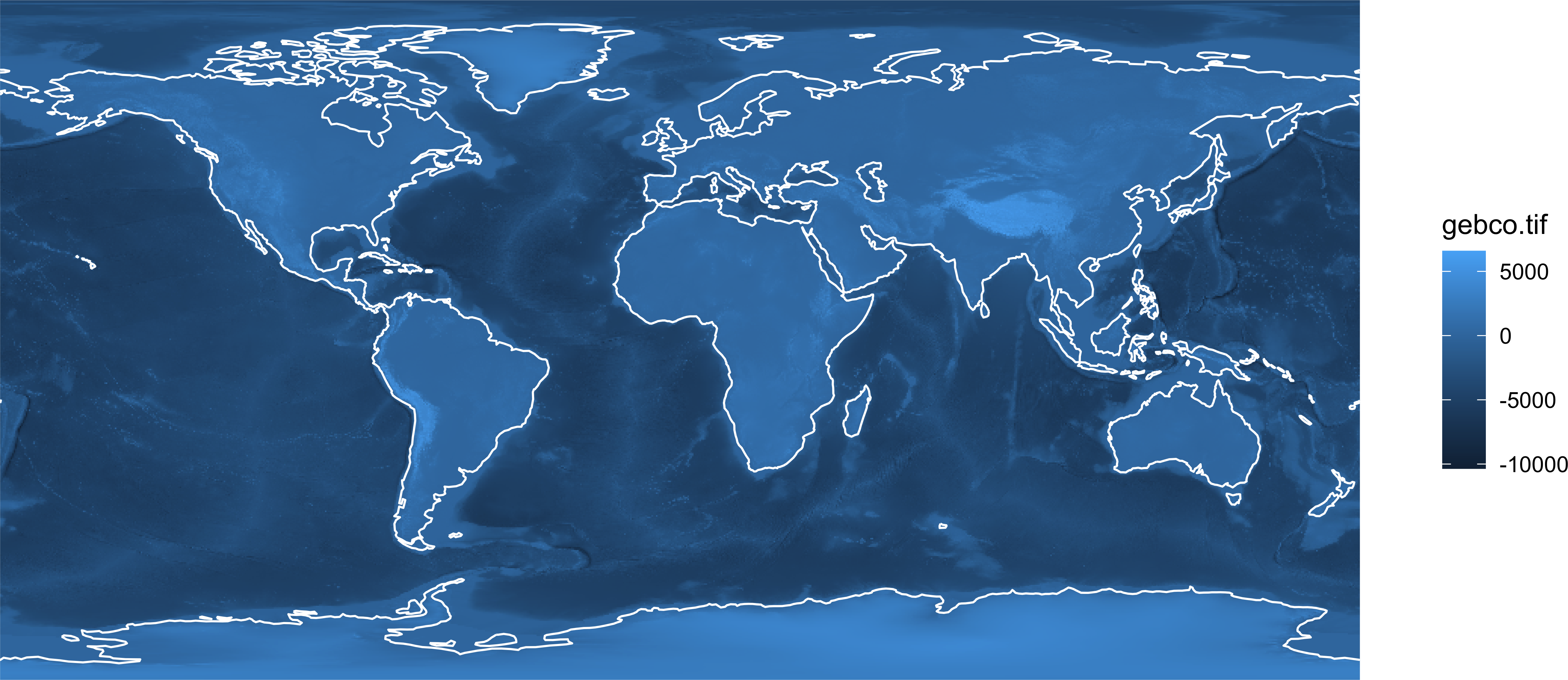

Для начала попробуем раскрасить рельеф в традиционной цветовой шкале, и посмотреть как это будет выглядеть:

pal = c('navyblue', 'steelblue', 'azure', 'darkslategray', 'olivedrab', 'lightyellow', 'firebrick', 'pink', 'white')

# Вынесем повторяющиемя слои в отдельный список
hydro_lyrs = list(
  geom_sf(data = lyr110$coast, linewidth = 0.4, color = 'steelblue4'),
  geom_sf(data = lyr110$rivers, linewidth = 0.3, color = 'steelblue4'),
  geom_sf(data = lyr110$lakes, linewidth = 0.3, color = 'steelblue4', fill = 'azure')
)

ggplot() +
  geom_stars(data = dem) +
  scale_fill_gradientn(colours = pal) +
  hydro_lyrs +
  coord_sf() +
  theme_void()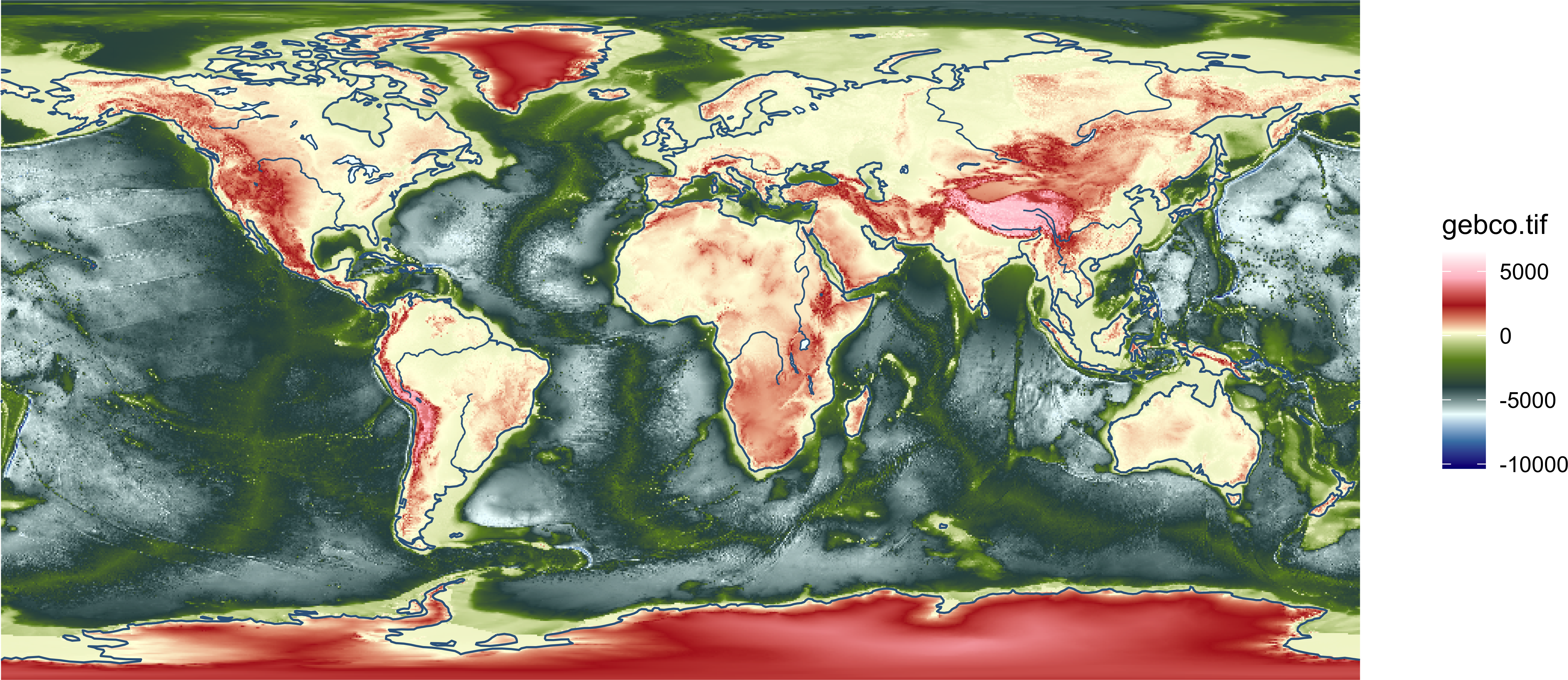

Видно, что по умолчаню цвета распределяются равномерно вдоль шкалы. Нам же необходимо ассоциировать их с конкретными высотами. Это можно сделать, определив в функции scale_fill_gradientn параметр values. Он принимает значения от 0 до 1 и указывает позицию цвета между минимумом и максимум. Чтобы сформировать такие позиции, необходимо сначала сделать гипсометрическую шкалу в метрах, а затем отмасштабировать ее на дипазон \([0, 1]\) посредством функции rescale из пакета scales:

val = c(min(dem[[1]]), -4000, -200, 0, 100, 300, 1000, 2500, max(dem[[1]])) |> 
  scales::rescale()

ggplot() +
  geom_stars(data = dem) +
  scale_fill_gradientn(colours = pal, values = val) +
  hydro_lyrs +
  coord_sf() +
  theme_void()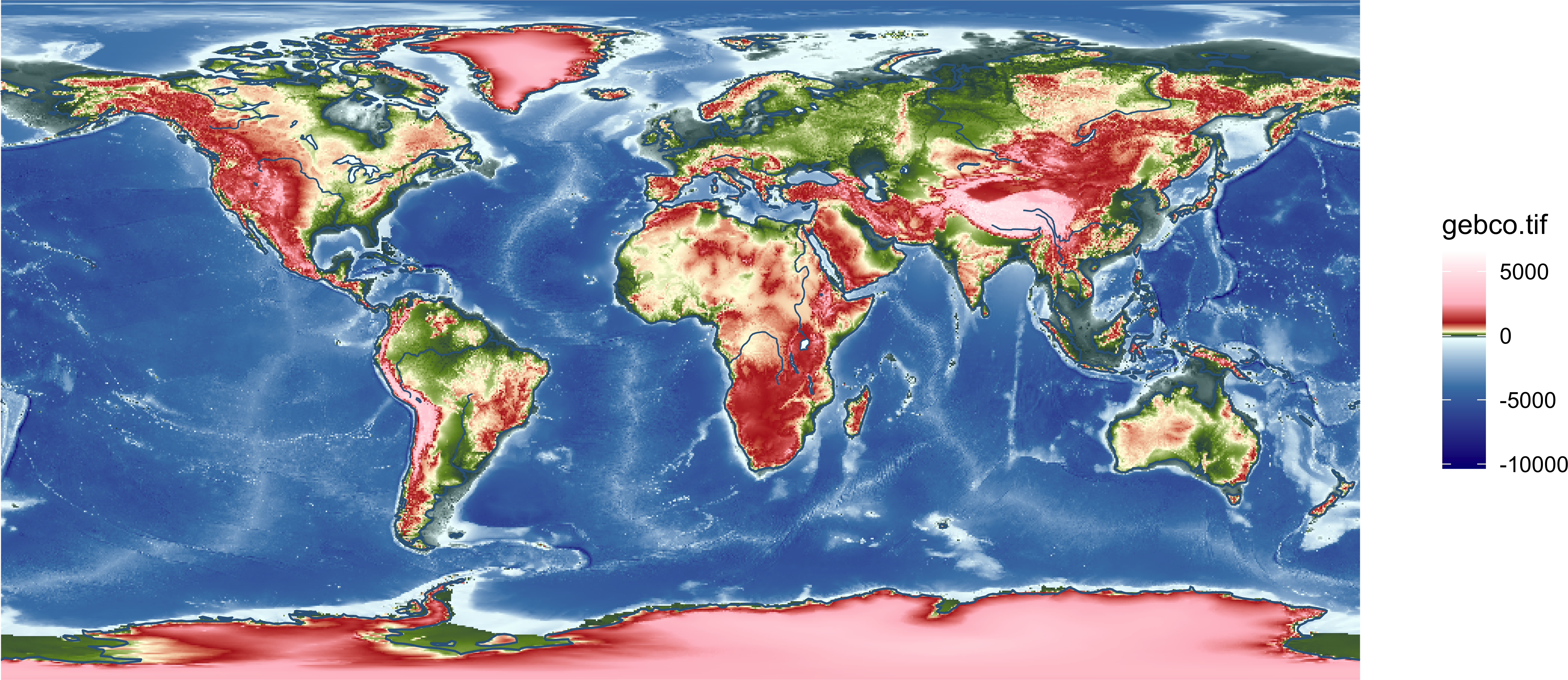

На первый взгляд может показаться, что все в порядке, но есть 2 проблемы: - отрицательные высоты на суше закрашиваются таким же цветом, как и отрицательные высота на море - нет резкого перехода через отметку 0, при котором цвет должен меняться с голубого на темно-зеленый.

Чтобы убедиться в этом рассмотрим фрагмент карты подробнее, обратив внимание на Персидский залив, Каспийское и Черное моря:

anno = list(
  annotate("rect", xmin = 45, xmax = 60, ymin = 22, ymax = 32, 
           color = 'white', linewidth = 2, fill = NA),
  annotate("rect", xmin = 45, xmax = 57, ymin = 35, ymax = 48, 
           color = 'white', linewidth = 2, fill = NA),
  annotate("rect", xmin = 26, xmax = 43, ymin = 40, ymax = 48, 
           color = 'white', linewidth = 2, fill = NA)
)

ggplot() +
  geom_stars(data = dem) +
  scale_fill_gradientn(colours = pal, values = val) +
  hydro_lyrs +
  anno +
  coord_sf(xlim = c(10, 75), ylim = c(20, 50)) +
  theme_void()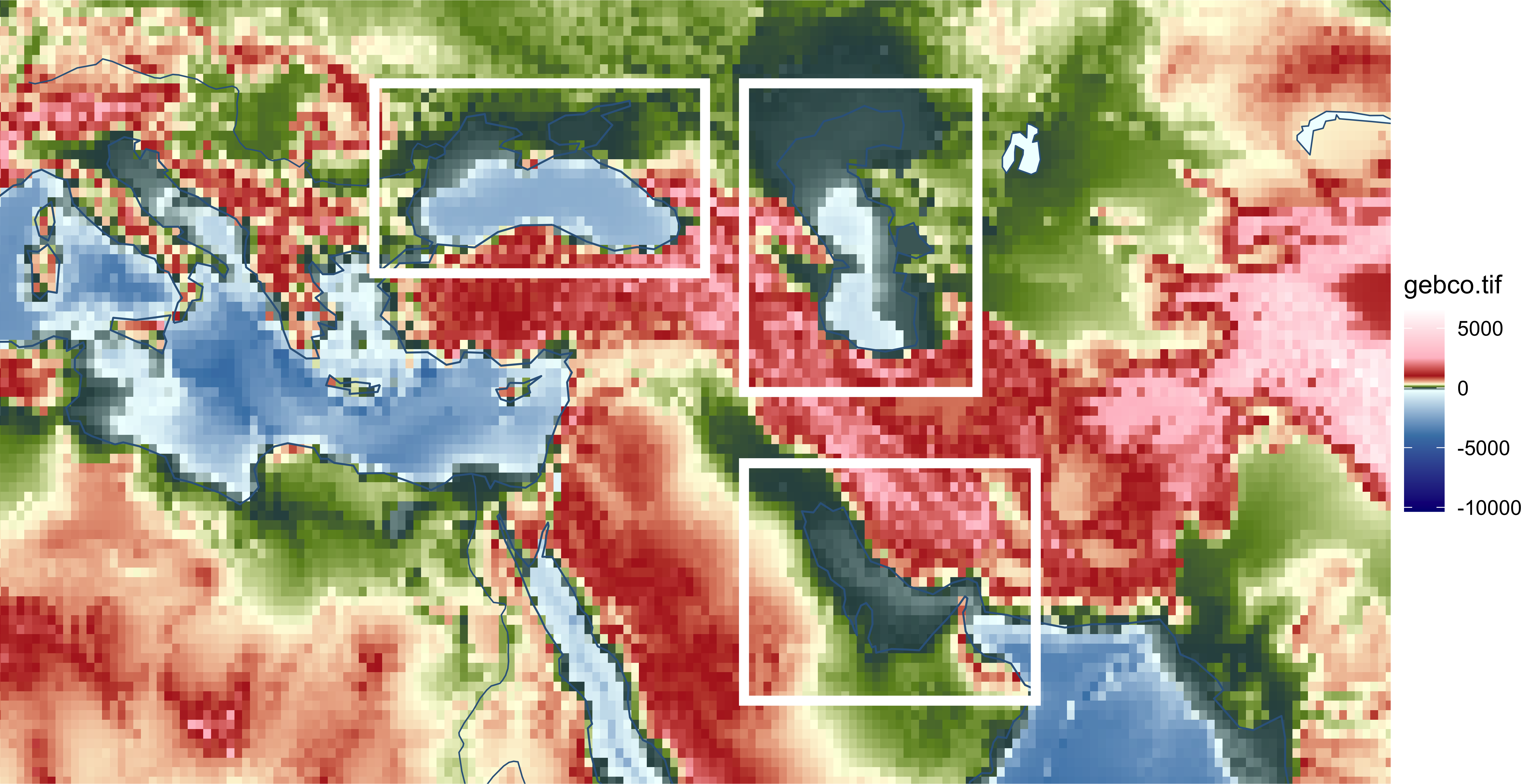

Чтобы не возникало такого эффекта, необходимо разделить цифровую модель рельефа на ldt: одна для суши, вторая для мора. Для этого используем стандартный синтаксис вида stars[sf], который позволяет обрезать объект типа stars заданным объектом типа sf:

sf_use_s2(FALSE)
dem_land = dem[lyr110$land]
dem_ocean = dem[lyr110$ocean]

map = ggplot() +
  geom_stars(data = dem_ocean) +
  scale_fill_gradientn(
    colours = c('navyblue', 'steelblue4', 'skyblue2', 'azure', 'azure'),
    values = scales::rescale(
      c(min(dem_ocean[[1]], na.rm = T), 
        -4000, -200, 0, 
        max(dem_ocean[[1]], na.rm = T))
    ),
    na.value = NA
  ) +
  new_scale_fill() +
  geom_stars(data = dem_land) +
  scale_fill_gradientn(
    colours = c('darkslategray', 'darkslategray', 'olivedrab', 
                'lightyellow', 'firebrick', 'pink', 'white'), 
    values = scales::rescale(
      c(min(dem_land[[1]], na.rm = T), 
        -50, 100, 300, 1500, 3500, 
        max(dem_land[[1]], na.rm = T)
      )
    ), 
    na.value = NA
  ) +
  hydro_lyrs +
  coord_sf() +
  theme_void()

map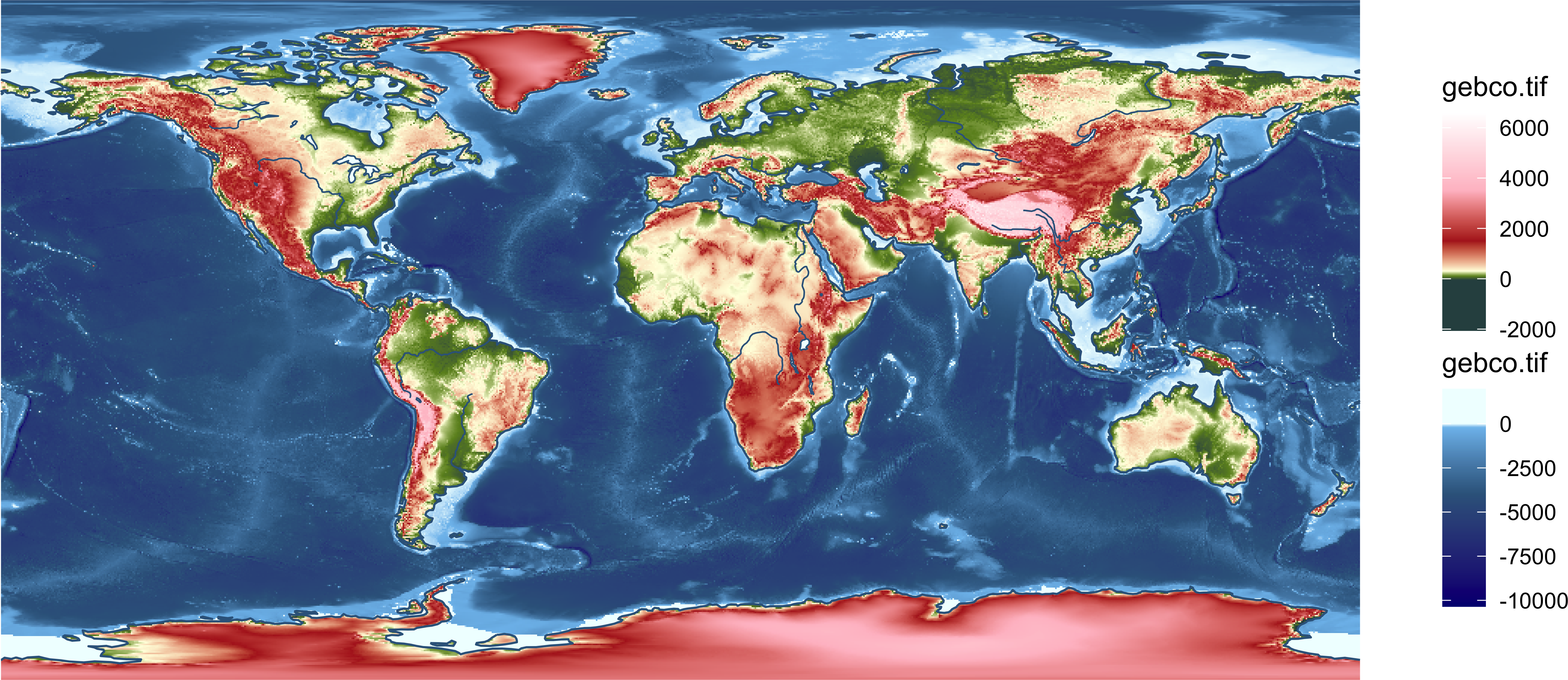

Проверим ранее указанную область:

map +
  coord_sf(xlim = c(10, 75), ylim = c(20, 50)) +
  anno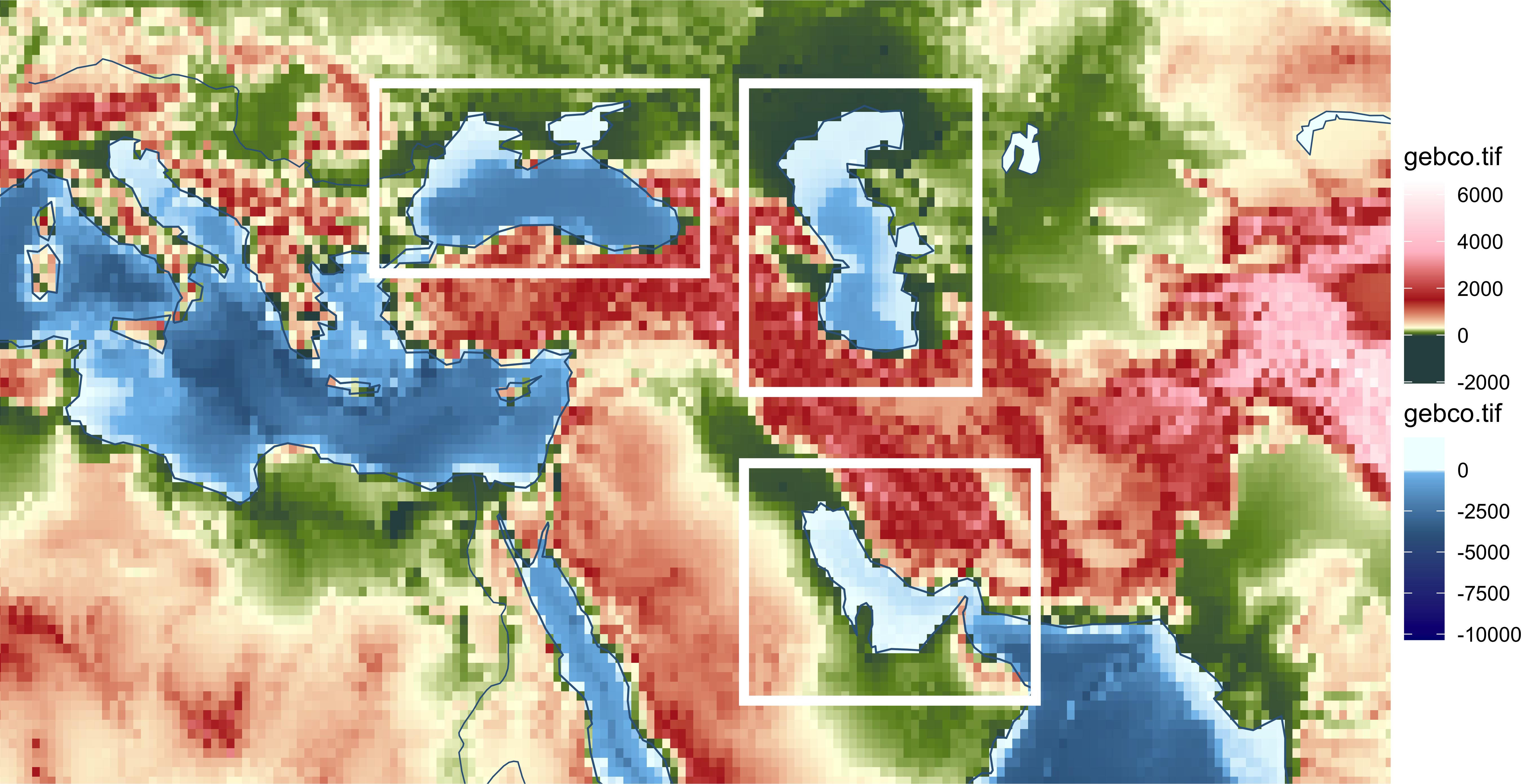

10.5.2 Проецирование растровых данных

В отличие от векторных данных, растровые необходимо трансформировать заранее в нужную проекцию. Для этого воспользуемся функцией st_warp:

hydro_lyrs = list(
  geom_sf(data = st_wrap_dateline(lyr110$coast), linewidth = 0.4, color = 'steelblue4'),
  geom_sf(data = st_wrap_dateline(lyr110$rivers), linewidth = 0.3, color = 'steelblue4'),
  geom_sf(data = st_wrap_dateline(lyr110$lakes), linewidth = 0.3, color = 'steelblue4', fill = 'azure')
)

prj = '+proj=eck3'

scale_ocean = scale_fill_gradientn(
    colours = c('navyblue', 'steelblue4', 'skyblue2', 'azure', 'azure'),
    values = scales::rescale(
      c(min(dem_ocean[[1]], na.rm = T), 
        -4000, -200, 0, 
        max(dem_ocean[[1]], na.rm = T))
    ),
    na.value = NA
  )

scale_land = scale_fill_gradientn(
    colours = c('darkslategray', 'darkslategray', 'olivedrab', 
                'lightyellow', 'firebrick', 'pink', 'white'), 
    values = scales::rescale(
      c(min(dem_land[[1]], na.rm = T), 
        -50, 100, 300, 1500, 3500, 
        max(dem_land[[1]], na.rm = T)
      )
    ), 
    na.value = NA
  )

ggplot() +
  geom_stars(data = st_warp(dem_ocean, crs = prj)) +
  scale_ocean +
  new_scale_fill() +
  geom_stars(data = st_warp(dem_land, crs = prj)) +
  scale_land +
  hydro_lyrs +
  coord_sf(crs = prj) +
  theme_void()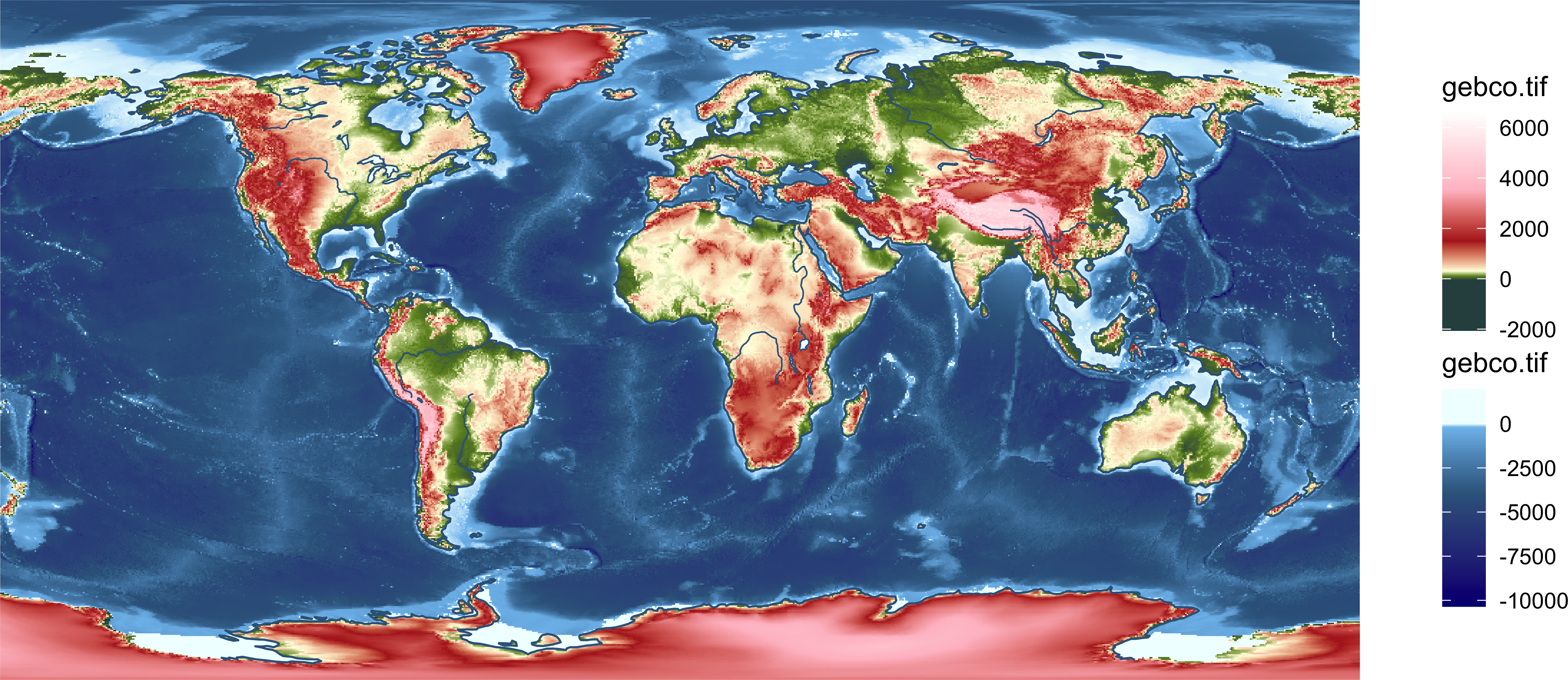

Обратим внимание, что растр проецируется немного не так, как векторные данные, его область остается прямоугольной. Поэтому при построении карт мира необходимо растры после проецирования обрезать прямоугольником, охватывающим весь мир:

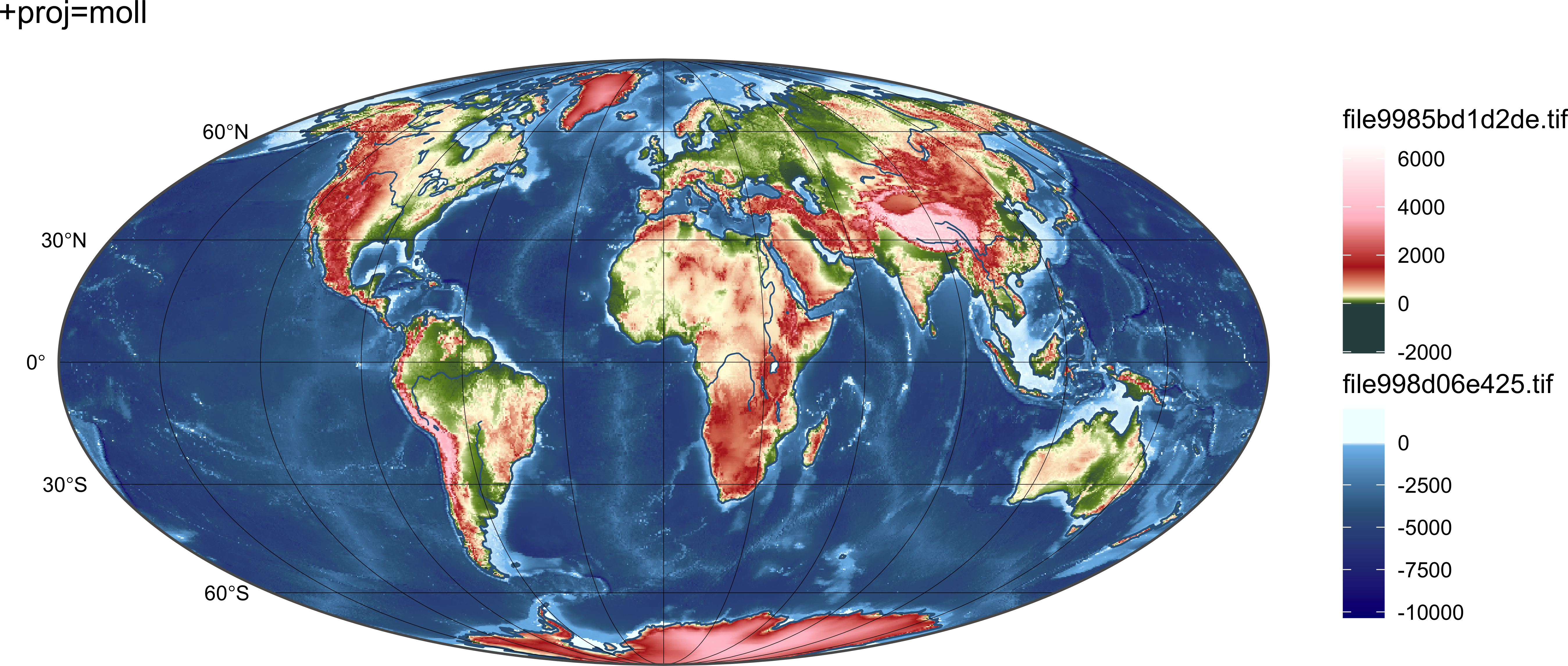
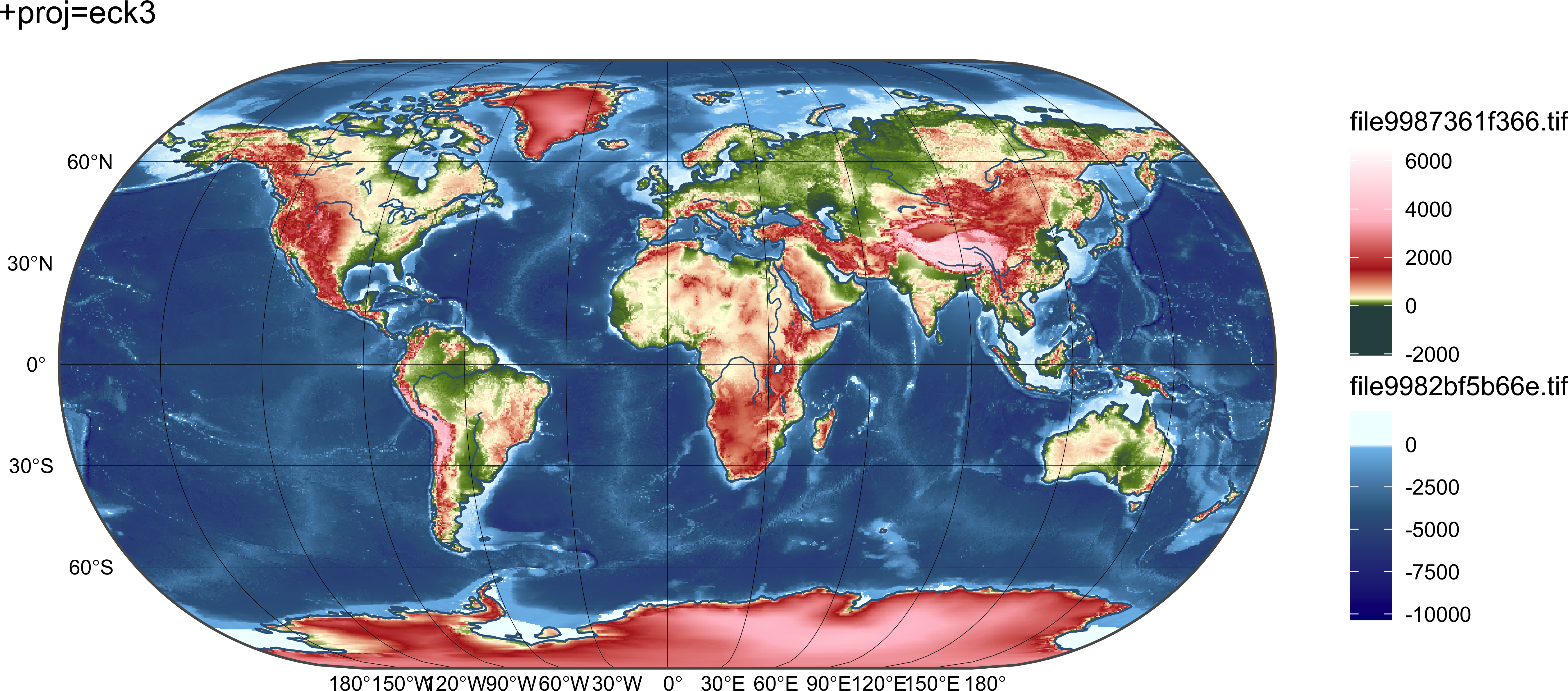
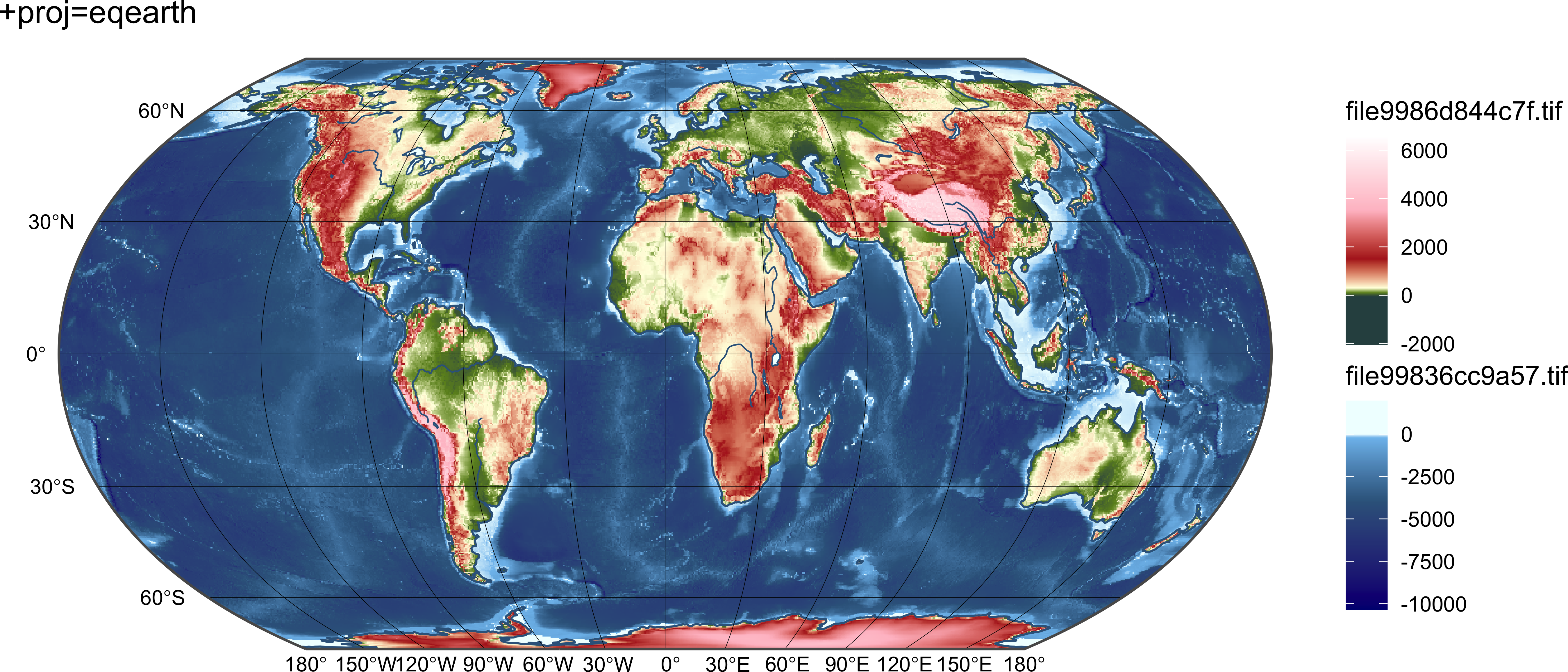
prjs = c("+proj=moll", "+proj=eck3", "+proj=eqearth", "+proj=times")
lon_labs = c(F,T,T,T)

for (i in seq_along(prjs)) {
  pbox = st_transform(box, prjs[i])

  map = ggplot() +
    geom_stars(data = st_warp(dem_ocean, crs = prjs[i], use_gdal = TRUE)[pbox]) +
    scale_ocean +
    new_scale_fill() +
    geom_stars(data = st_warp(dem_land, crs = prjs[i], use_gdal = TRUE)[pbox]) +
    scale_land +
    hydro_lyrs +
    geom_sf(data = grat, linewidth = 0.1) +
    geom_sf(data = box, linewidth = 0.5, fill = NA) +
    coord_sf(crs = prjs[i]) +
    degree_labels(grat, vjust = +1.5, hjust = +1.5, size = 3, lon = lon_labs[i]) +
    ggtitle(prjs[i]) +
    theme_void()
  
  print(map)
}

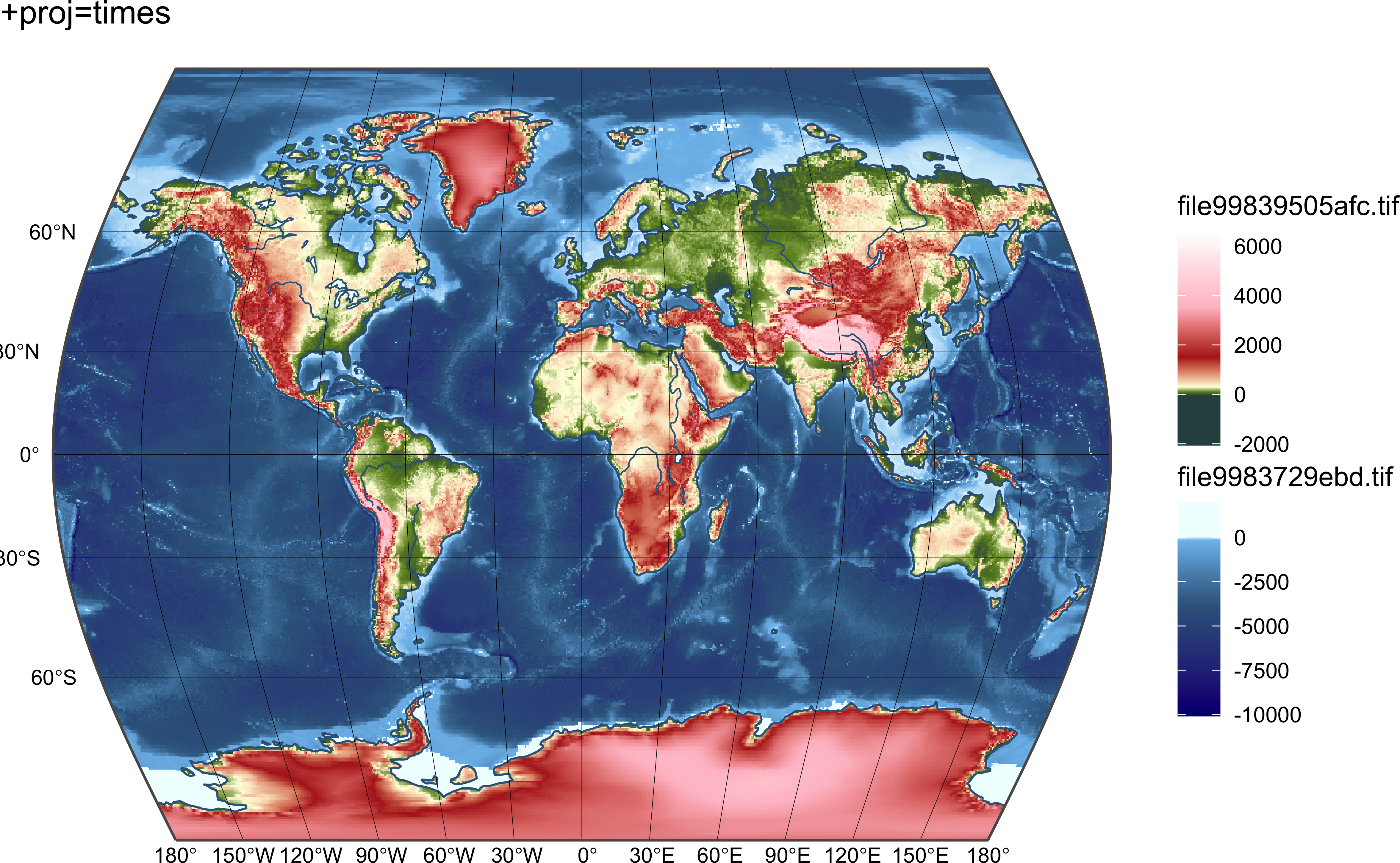
10.6 Детализация данных

10.6.1 Выбор картографической основы

Один из обязательных признаков хорошей карты — это использование пространственных данных подходящей детализации. Избыточная детализация приводит к тому, что карта становится неопрятной, пестрит трудно воспринимаемыми деталями, производит непрофессиональное впечатление. Помимо этого, избыточная детализация данных приводит к тому, что карта будет медленно прорисовываться. Это справедливо как для карт, создаваемых программным путём, так и для карт, которые составляются в ГИС-пакетах. В некоторых случаях можно столкнуться с обратной ситуацией, когда данные менее детальны, чем это требуется для карты. В этом случае у пользователя карты будет складываться впечатление, что карта недостаточно точна и информативна.

Проблема детализации касается в основном картографической основы, поскольку подбирается она прежде всего в соответствии с охватом исследуемой территории и физическим размером итогового изображения. В случае если предполагается совмещение картографической основы и тематических данных, важным фактором будет также детализация самих тематических данных.

В качестве примера для выбора подходящей основы рассмотрим задачу построения карты Европы, которая бы вписывалась в размер страницы данной книги. База данных Natural Earth содержит 3 уровня детализации, из которых надо выбрать подходящий. Сравним их:

cnt010 = st_read(ne, 'ne_10m_admin_0_countries', quiet = T)
cnt050 = st_read(ne, 'ne_50m_admin_0_countries', quiet = T)
cnt110 = st_read(ne, 'ne_110m_admin_0_countries', quiet = T)

prj = '+proj=laea +lat_0=50 +lon_0=10'

box = st_bbox(c(xmin = -10, xmax = 33, 
                ymin = 33, ymax = 60),
              crs = st_crs(4326)) |> 
  st_as_sfc() |> 
  st_transform(prj) |> 
  st_bbox()

cnts = list(cnt010, cnt050, cnt110)
scales = c(10, 50, 110)

for (i in seq_along(cnts)) {
  print(
      ggplot() +
        geom_sf(data = cnts[[i]], linewidth = 0.25,
                mapping = aes(fill = as.factor(MAPCOLOR7)),
                show.legend = FALSE) +
        scale_fill_manual(values = brewer.pal(7, 'Set2')) +
        coord_sf(crs = prj, 
                 xlim = c(box[1], box[3]),
                 ylim = c(box[2], box[4])) +
        theme_bw() +
        theme(panel.background = element_rect(fill = 'azure')) +
        ggtitle(glue::glue('Уровень детализации {scales[i]}M'))
  )
}

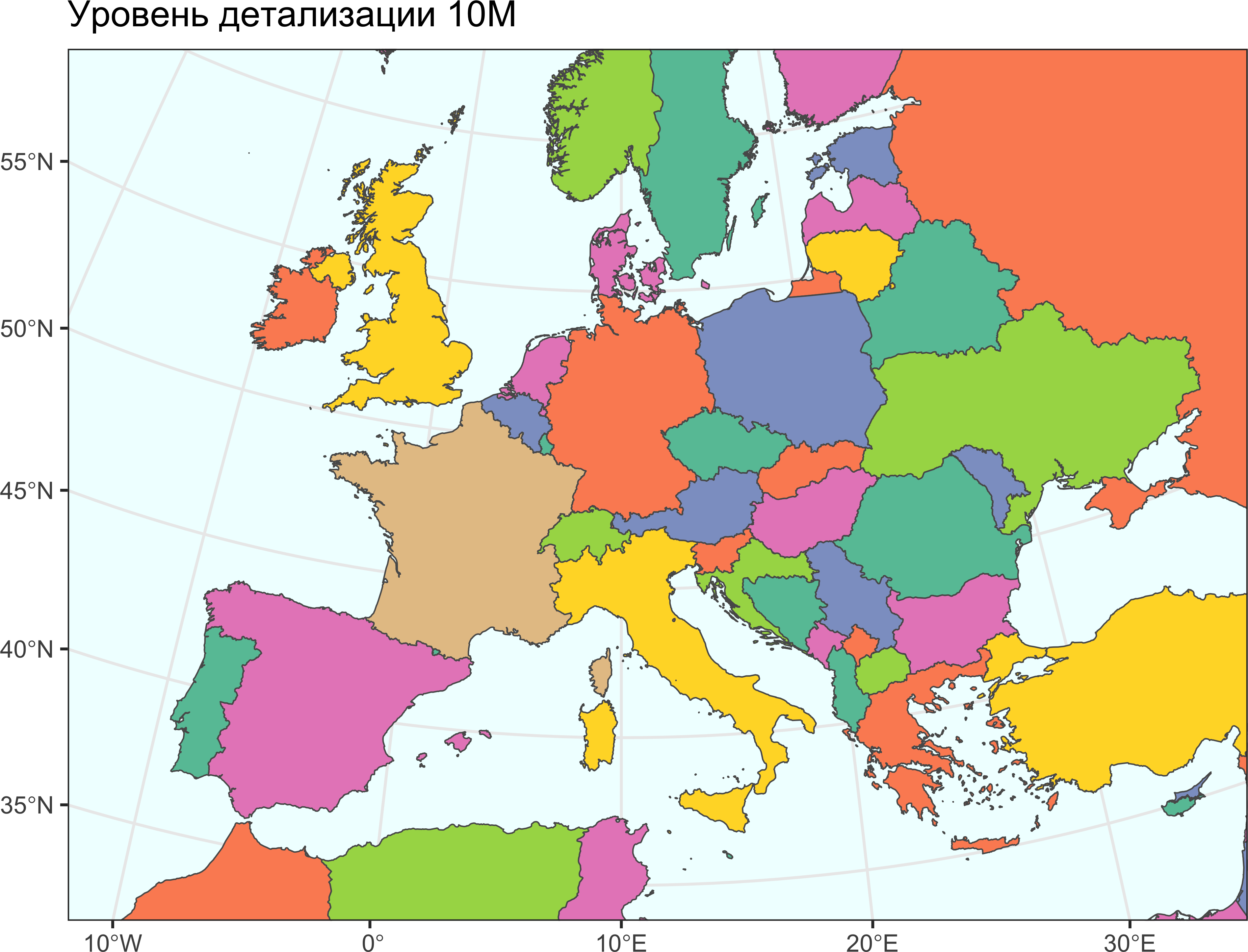
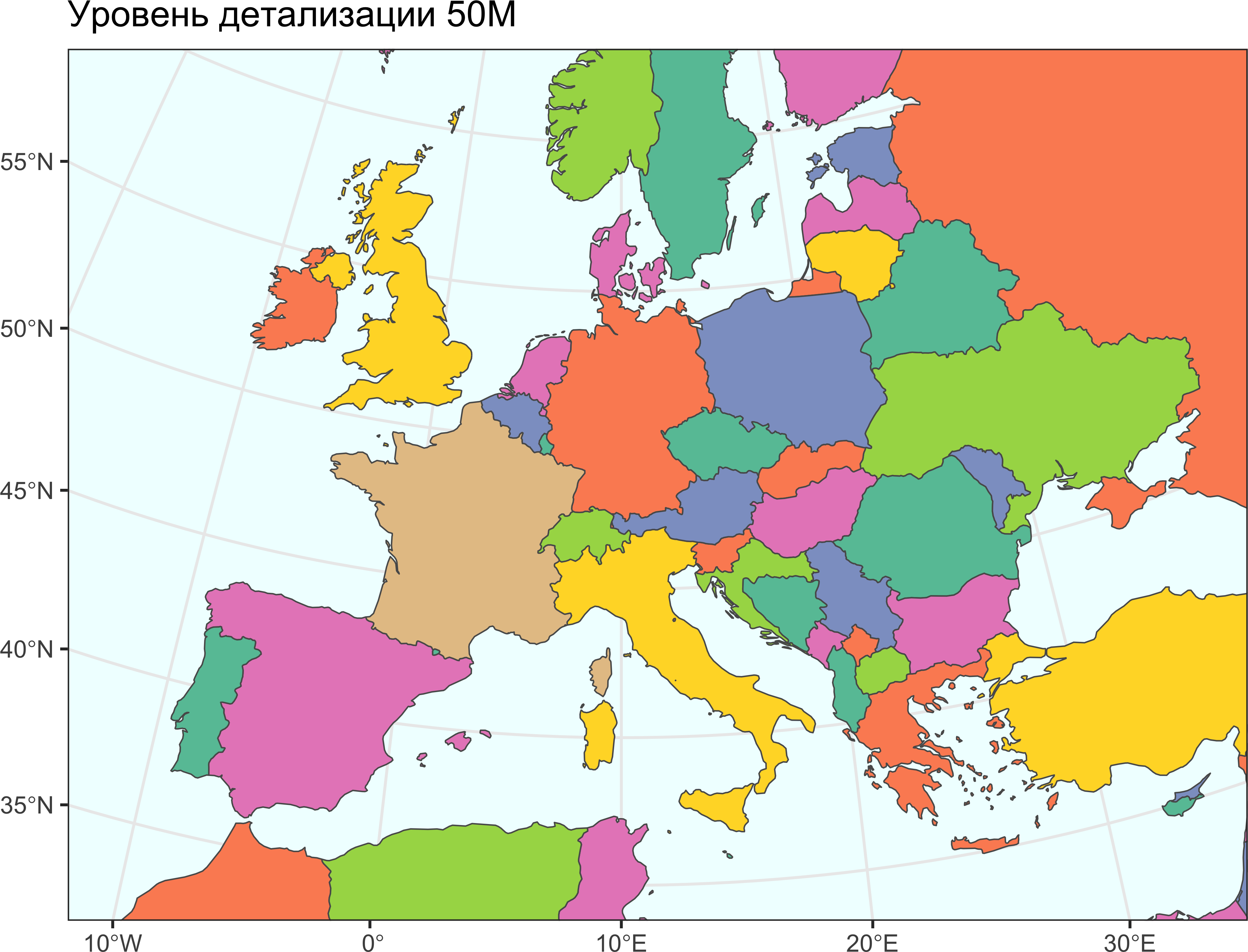
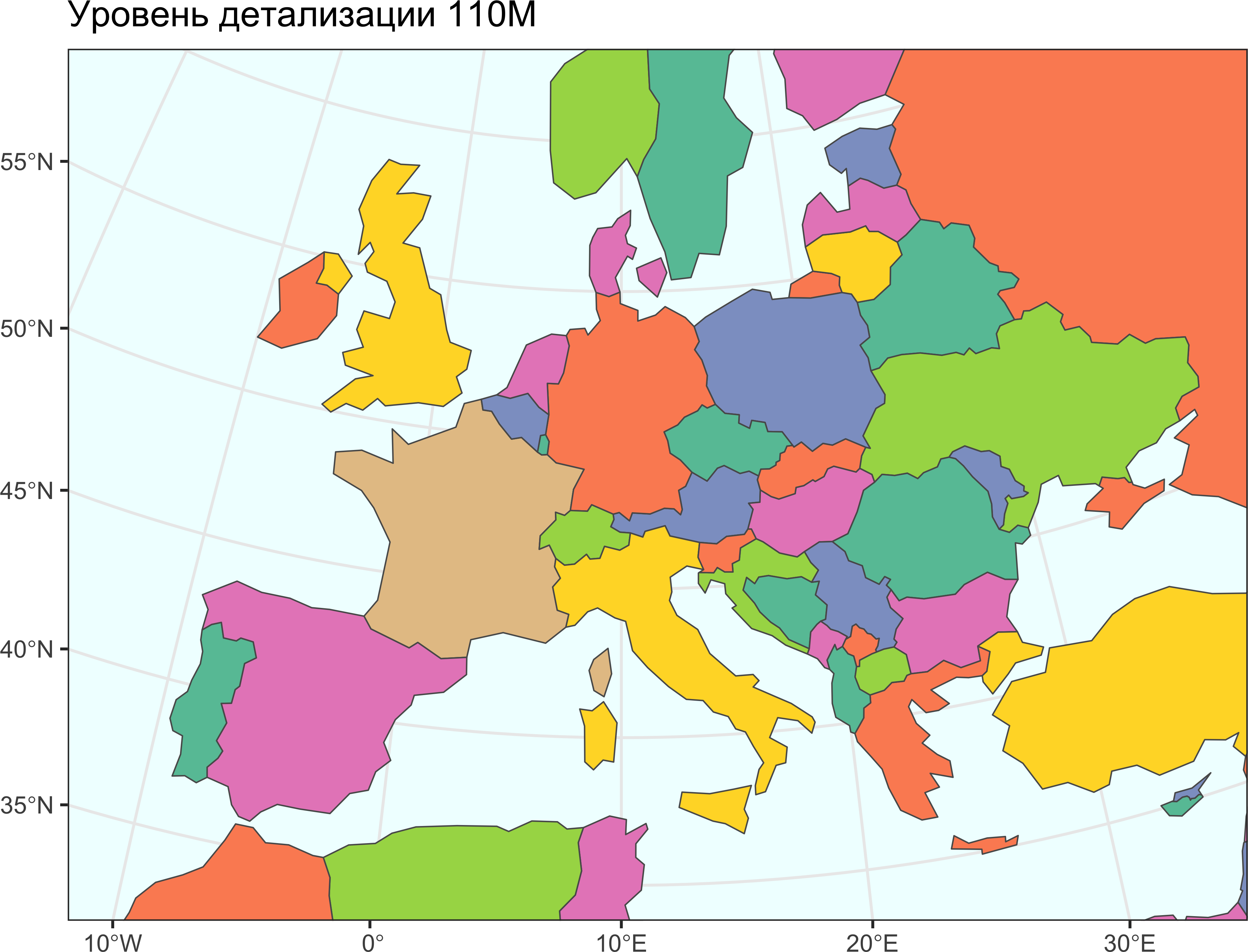
Очевидно, что в данном случае оптимальным является средний уровень детализации 50M. Два других уровня при выбранном охвате территории и размере карты являются либо избыточно (10M), либо недостаточно (110M) детальными.

10.6.2 Генерализация картографической основы

Иногда не удается найти картографическую основу подходящей детализации. В этом случае вы можете провести генерализацию данных. Поскольку генерализация является достаточно ресурсоемкой процедурой, ее не следует проводить непосредственно в скрипте, который занимается построением карт. Вместо этого, необходимо вынести создание генерализованной картографической основы в отдельный скрипт. Наиболее часто в целях генерализации используются такие операции как геометрическое упрощение и отбор объектов. Следует, однако, помнить, что эти процедуры целесообразно выполнять после того как данные трансформированы в нужную проекцию. В противном случае генерализация может быть неравномерной по полю карты (один градус долготы соответствует меньшим расстояниям в близости полюсов). Помимо этого, будет сложно выполнять параметризацию алгоритмов генерализации.

10.6.2.1 Геометрическое упрощение

В качестве примера рассмотрим геометрическое упрощение рек и полигонов государств. Визуализируем для начала исходные данные:

countries = cnt010 |> 
  st_transform(prj) |> 
  st_crop(box)

ggplot() +
  geom_sf(data = countries, linewidth = 0.25) +
  ggtitle('Исходные данные масштаба 10M') +
  theme_minimal()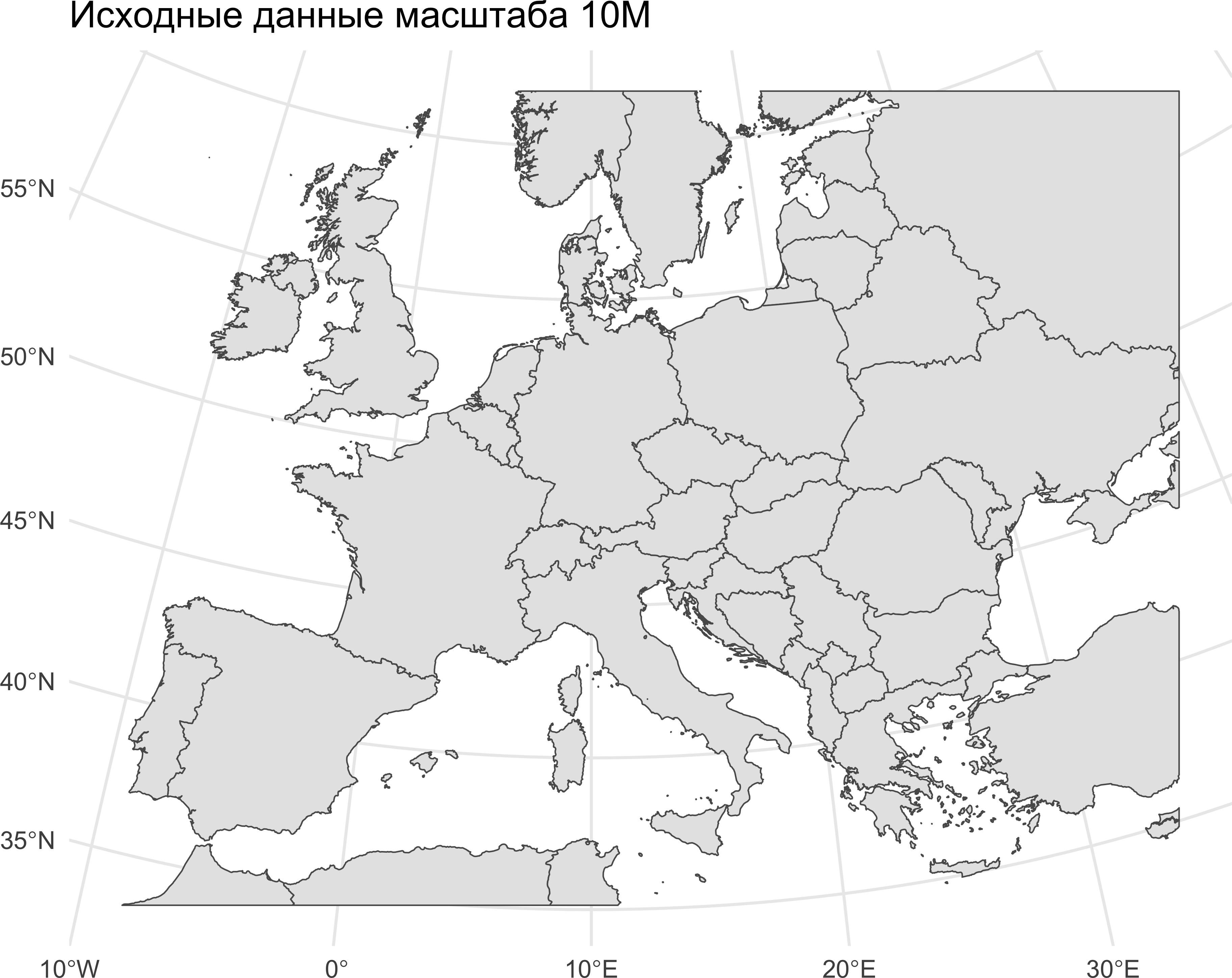

Невооруженным взглядом видно, что их детализация избыточна. Для геометрического упрощения воспользуемся функцией ms_simplify() из пакета rmapshaper. В данной функции доступно два алгоритма геометрического упрощения: Дугласа-Пейкера и Висвалингам-Уайатта. Принципы работы этих алгоритмов разные, поэтому сопоставимая детализация достиагается в них при разном количестве точек:

countries_dp = ms_simplify(countries, 
                           method = 'dp', # алгоритм Дугласа-Пейкера
                           keep = 0.04) # оставить 4% точек

countries_vw = ms_simplify(countries,  
                           method = 'vis', # алгоритм Висвалингам-Уайатта
                           keep = 0.06)  # оставить 6% точек

ggplot() +
  geom_sf(data = countries_dp, linewidth = 0.25) +
  ggtitle('Геометрическое упрощение алгоритмом Дугласа-Пейкера') +
  theme_minimal()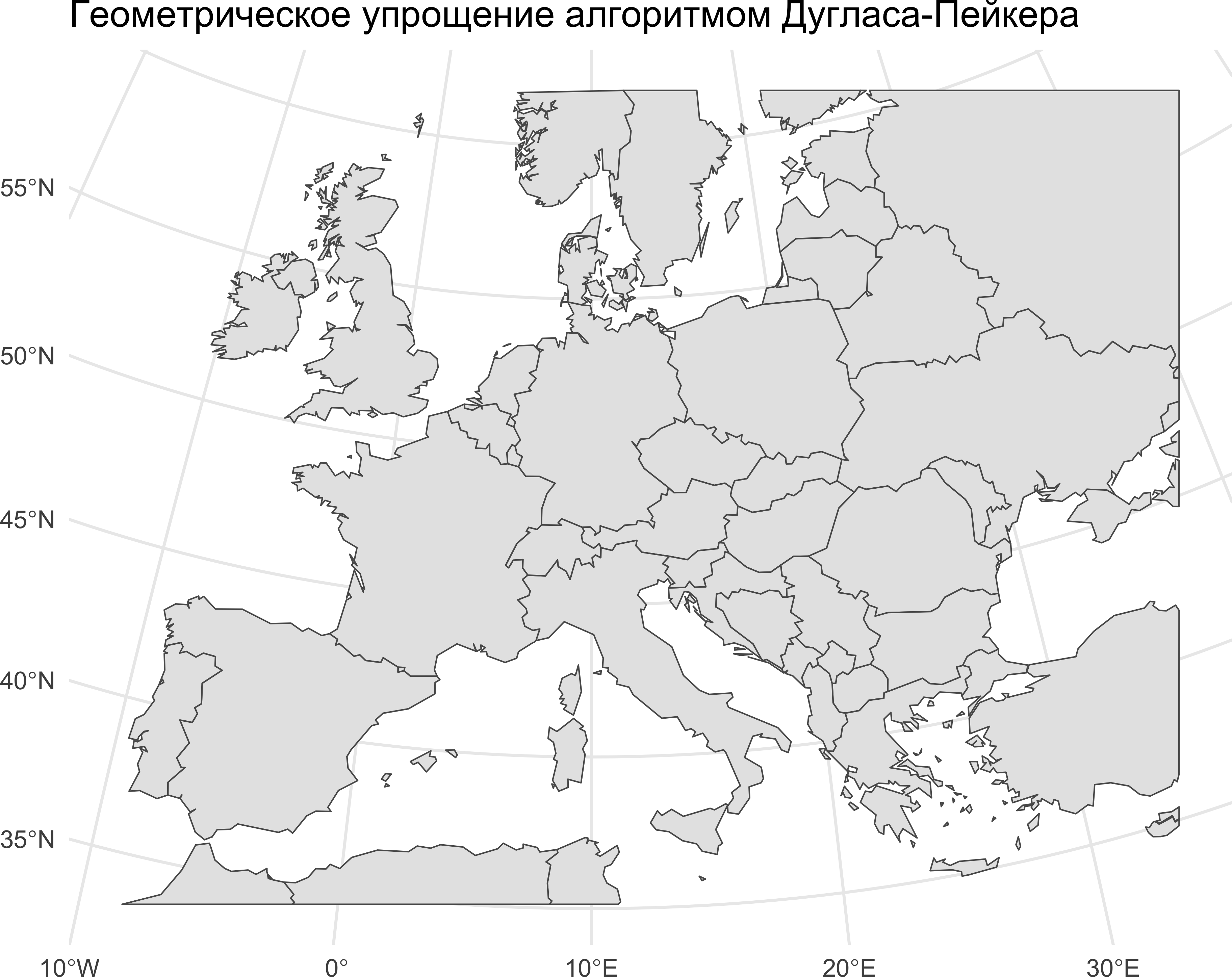

ggplot() +
  geom_sf(data = countries_vw, linewidth = 0.25) +
  ggtitle('Геометрическое упрощение алгоритмом Висвалингам-Уайатта') +
  theme_minimal()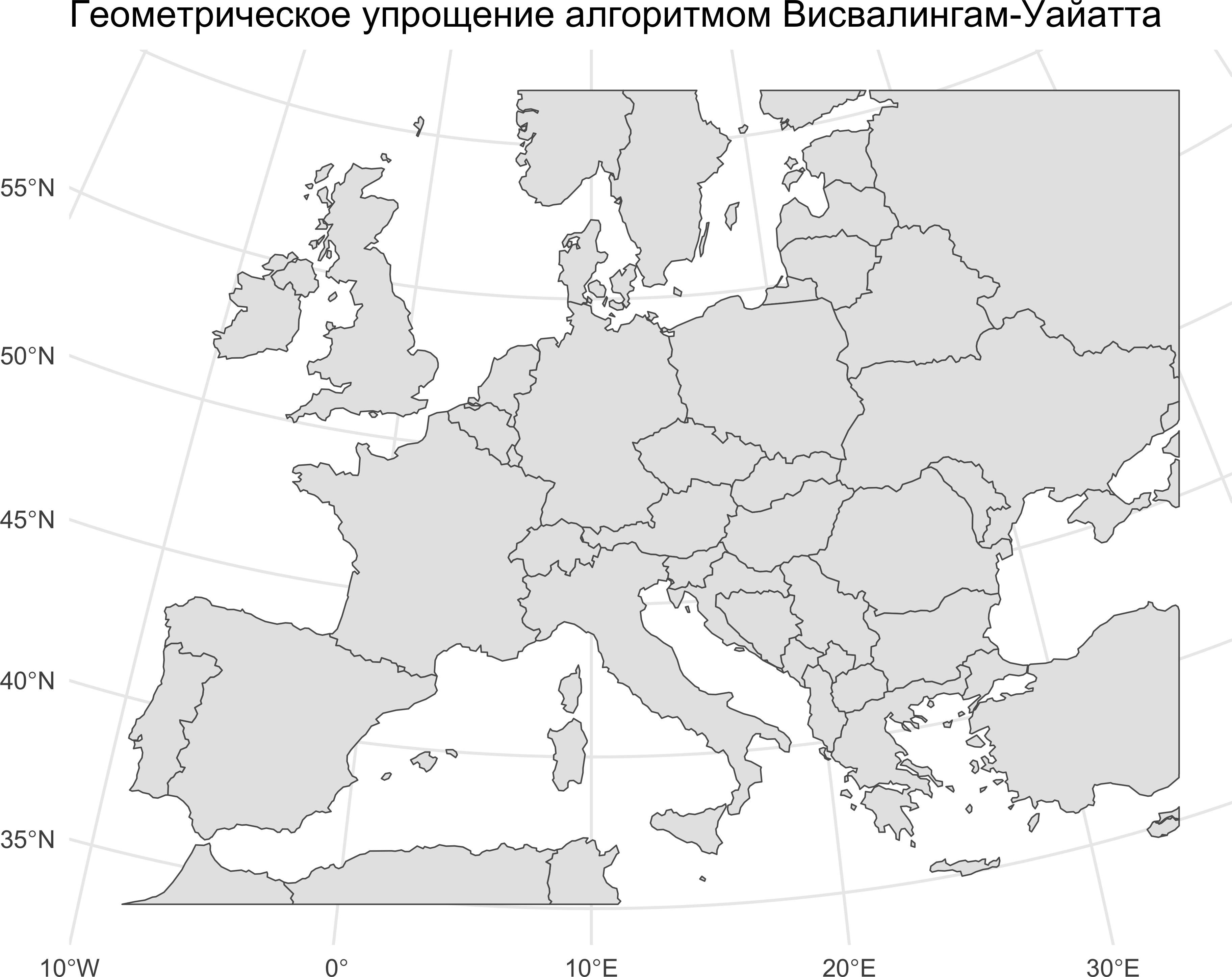

Видно, что результаты упрощения алгоритмом Дугласа-Пейкера довольно угловатые и неестественные. Но при этом он лучше сохраняет различные характерные точки в структуре линии типа вершин фьордов. Тем не менее для целей картографической генерализации алгоритм Висвалингам-Уайатта можно назвать предпочтительным.

Помимо этого, при геометрическом упрощении возникаеют сложности топологического согласования с другими слоями. Обратим внимание на то, как речки согласуются с береговой линией:

rivers = st_read(ne, 'ne_10m_rivers_lake_centerlines') |> 
  st_transform(prj) |> 
  st_crop(box) |> 
  st_cast('MULTILINESTRING') |> 
  st_cast('LINESTRING')
## Reading layer `ne_10m_rivers_lake_centerlines' from data source 
##   `/Volumes/Data/Spatial/Natural Earth/natural_earth_vector.gpkg' 
##   using driver `GPKG'
## Simple feature collection with 1473 features and 38 fields
## Geometry type: MULTILINESTRING
## Dimension:     XY
## Bounding box:  xmin: -164.9035 ymin: -52.15775 xmax: 177.5204 ymax: 75.79348
## Geodetic CRS:  WGS 84

ggplot() +
  geom_sf(data = countries_vw, linewidth = 0.25) +
  geom_sf(data = rivers, linewidth = 0.25, color = 'steelblue') +
  ggtitle('Геометрическое упрощение алгоритмом Висвалингам-Уайатта') +
  theme_minimal()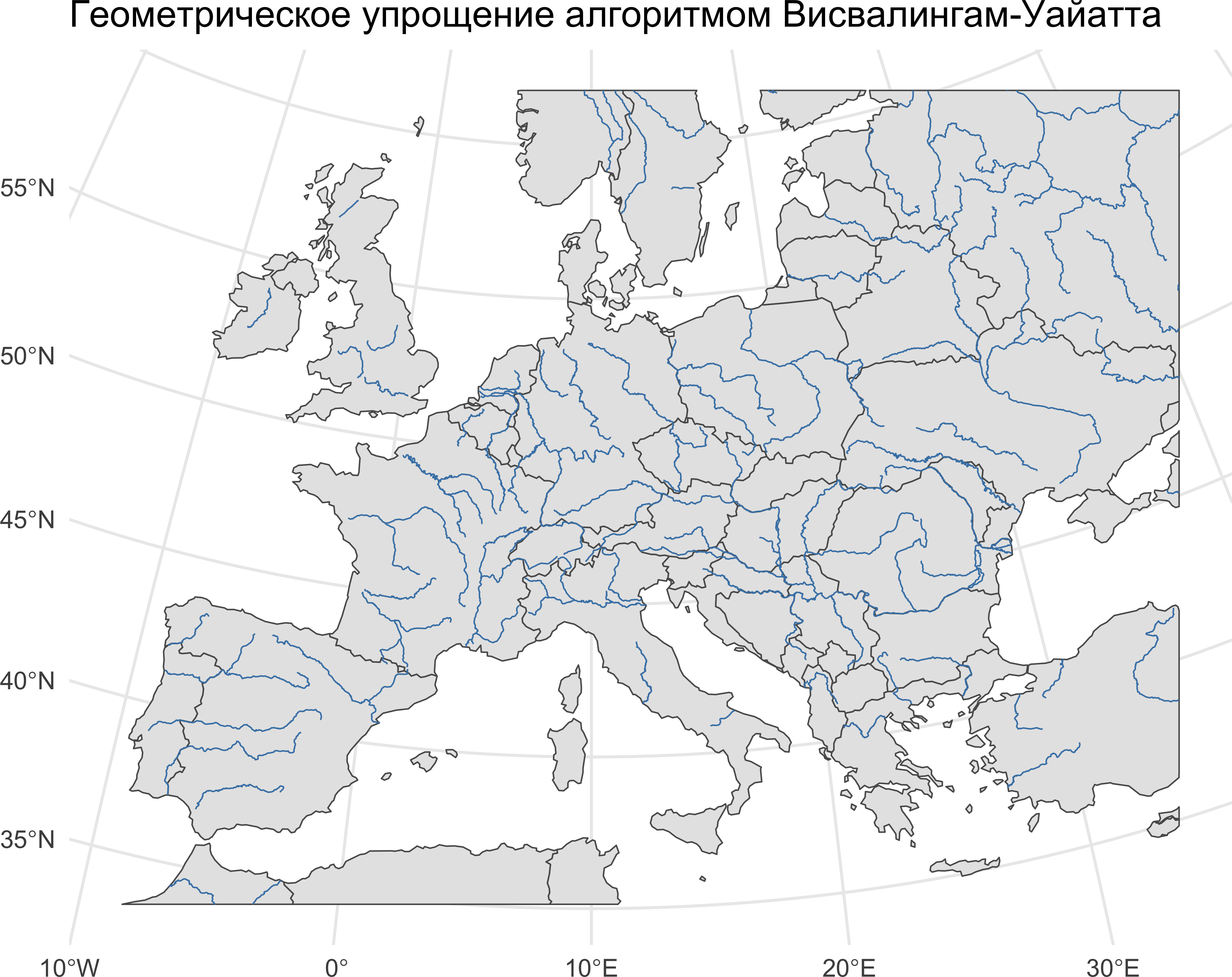

Здесь видно, что изза упрощения линий удалились эстуарии рек, и теперь речки не дотягивают до своих устьев. Чтобы такого эффекта не происходило, необходимо зафиксировать вершины эстуариев, запретив их удалять. Наиболее просто это сделать в линейном варианте, когда упрощению подвергаются береговые линии, а не полигоны стран:

coast = st_read(ne, 'ne_10m_coastline') |> 
  st_transform(prj) |> 
  st_crop(box) |>
  st_cast('MULTILINESTRING') |> 
  st_cast('LINESTRING') 
## Reading layer `ne_10m_coastline' from data source 
##   `/Volumes/Data/Spatial/Natural Earth/natural_earth_vector.gpkg' 
##   using driver `GPKG'
## Simple feature collection with 4133 features and 3 fields
## Geometry type: LINESTRING
## Dimension:     XY
## Bounding box:  xmin: -180 ymin: -85.22194 xmax: 180 ymax: 83.6341
## Geodetic CRS:  WGS 84

mouths = rivers |> 
  st_line_sample(ls, sample = c(1)) |> 
  st_cast('POINT') |> 
  st_snap(coast, tol = 1000) |> 
  st_intersection(coast)

ggplot() +
  geom_sf(data = coast, linewidth = 0.35, color = 'steelblue') +
  geom_sf(data = rivers, linewidth = 0.25, color = 'steelblue') +
  geom_sf(data = mouths, color = 'red') +
  theme_minimal()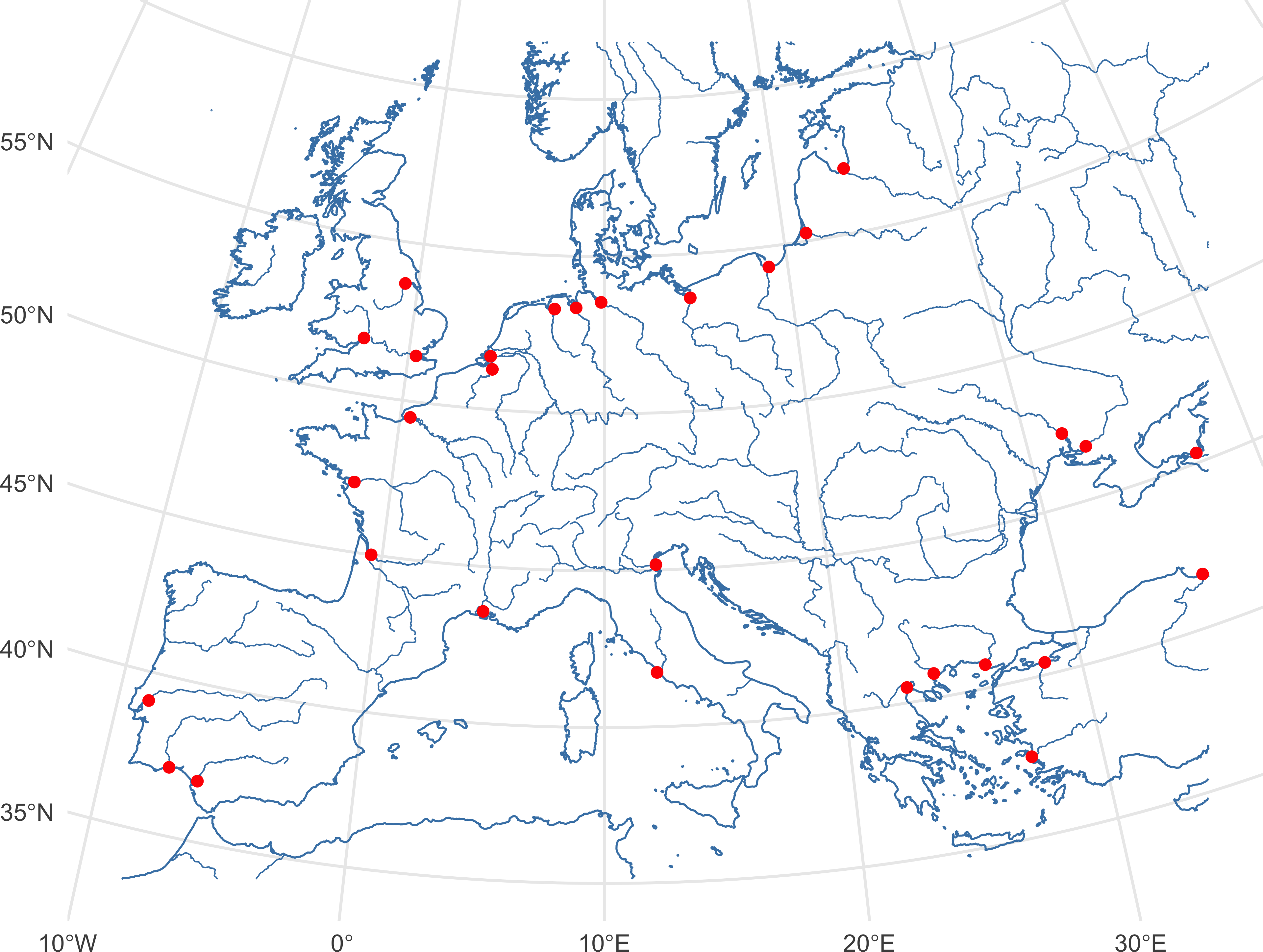

coast_split = lwgeom::st_split(coast, mouths) |> 
  st_collection_extract('LINESTRING')

coast_vw = ms_simplify(coast_split,  
                       method = 'vis', # алгоритм Висвалингам-Уайатта
                       keep = 0.05)  # оставить 6% точек

rivers_vw = ms_simplify(rivers,  
                       method = 'vis', # алгоритм Висвалингам-Уайатта
                       keep = 0.05)  # оставить 6% точек


ggplot() +
  geom_sf(data = coast_vw, linewidth = 0.35, color = 'steelblue') +
  geom_sf(data = rivers_vw, linewidth = 0.25, color = 'steelblue') +
  ggtitle('Геометрическое упрощение алгоритмом Висвалингам-Уайатта') +
  theme_minimal()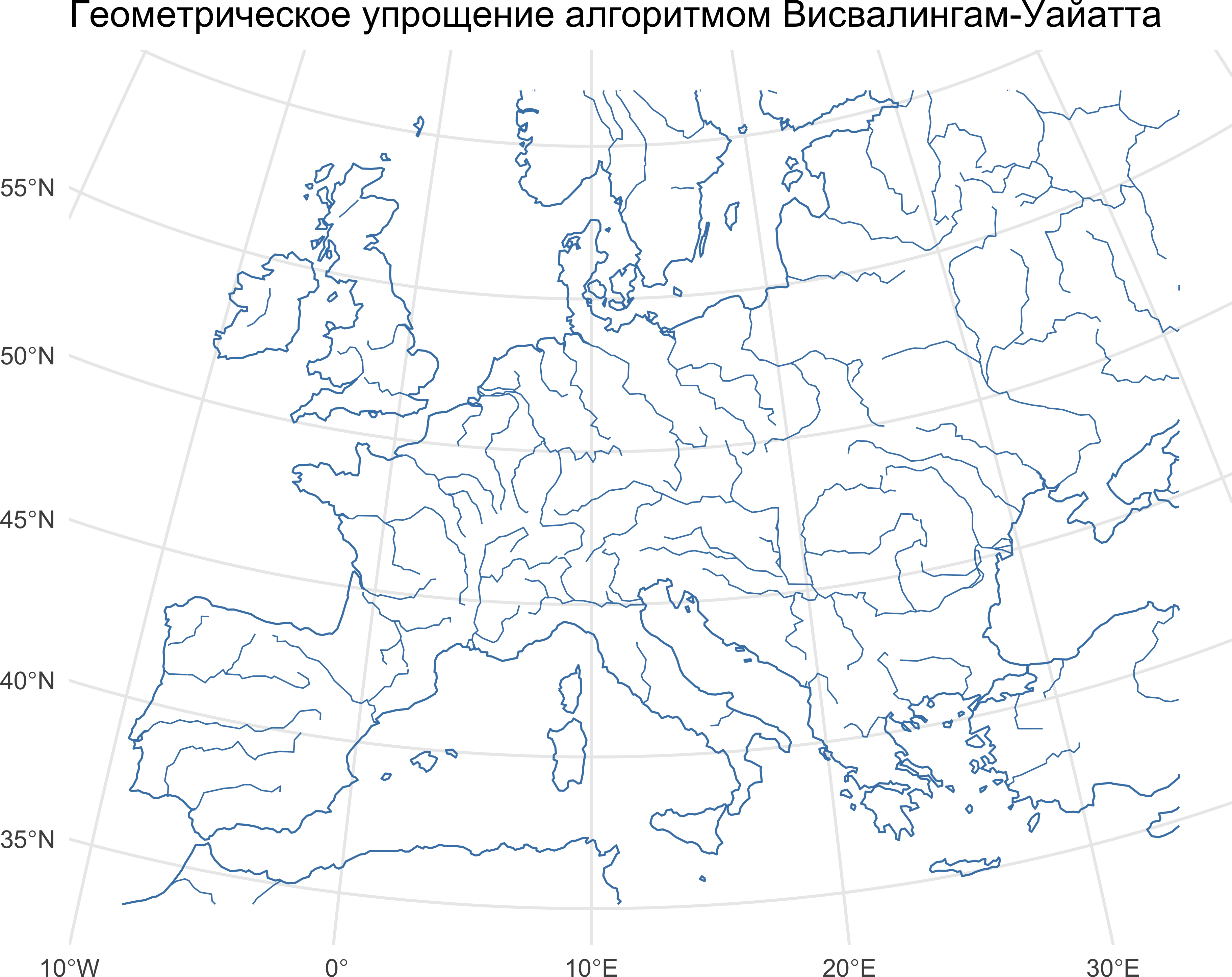

10.6.2.2 Отбор

Отбор применятся внутри множества пространственных объектов для того чтобы уменьшить их количество. Наиболее просто реализуется отбор для объектов, которые не состоят в пространственных отношениях. Как правило, это точечные объекты. Более сложна процедура отбора во множестве топологически связанных объектов. Например, прореживание транспортной или гидрографической сети. В данном разделе мы посмотрим как можно отбирать точечные объекты. Наиболее простой случай реализуется тогда, когда объекты можно отобрать по атрибутам, без использования пространственных отношений. К счастью, данные Natural Earth содержат атрибуты, которые можно использовать в качестве критериев отбора.

Для начала попробуем нанести все населенные пункты:

cities_eu = st_read(ne, 'ne_10m_populated_places') |> 
  st_transform(prj) |> 
  st_crop(box)
## Reading layer `ne_10m_populated_places' from data source 
##   `/Volumes/Data/Spatial/Natural Earth/natural_earth_vector.gpkg' 
##   using driver `GPKG'
## Simple feature collection with 7342 features and 137 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: -179.59 ymin: -90 xmax: 179.3833 ymax: 82.48332
## Geodetic CRS:  WGS 84

ggplot() +
  geom_sf(data = countries_vw, linewidth = 0.25) +
  geom_sf(data = cities_eu, size = 0.5, color = 'darkviolet') +
  geom_sf_text(data = cities_eu, 
               mapping = aes(label = NAME),
               size = 1.5, nudge_y = 30000) +
  theme_bw()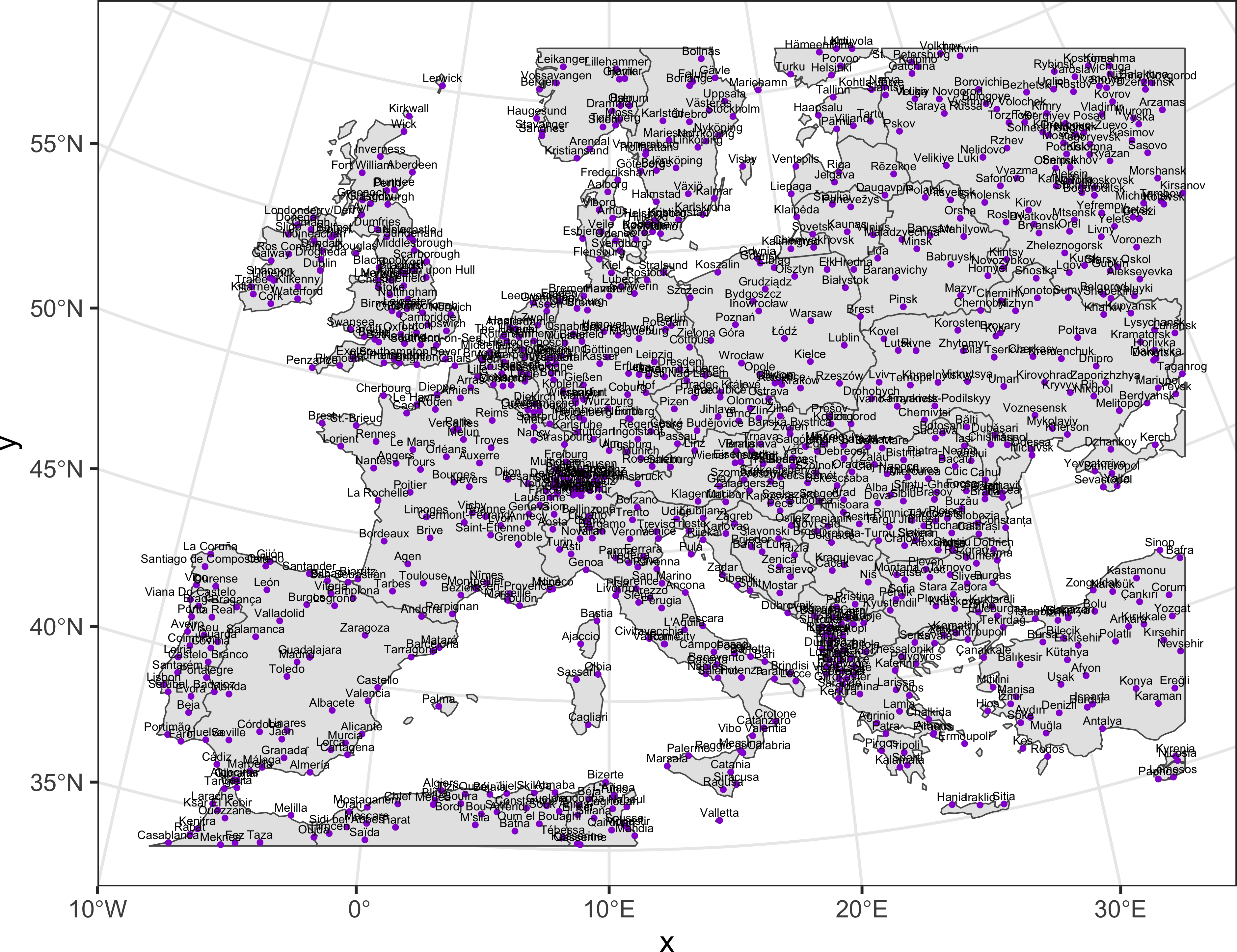

Очевидно, что при такой плотности нормальную карту составить не получится. Попробуем для начала остаить только столицы и разнести их через ggrepel:

capitals = filter(cities_eu, FEATURECLA == 'Admin-0 capital')

ggplot() +
  geom_sf(data = countries_vw, linewidth = 0.25) +
  geom_sf(data = capitals, size = 1.2, color = 'darkviolet') +
  geom_text_repel(data = capitals, stat = "sf_coordinates",
                size = 2.5, aes(label = NAME, geometry = geom), 
                fontface = 'bold') +
  theme_bw()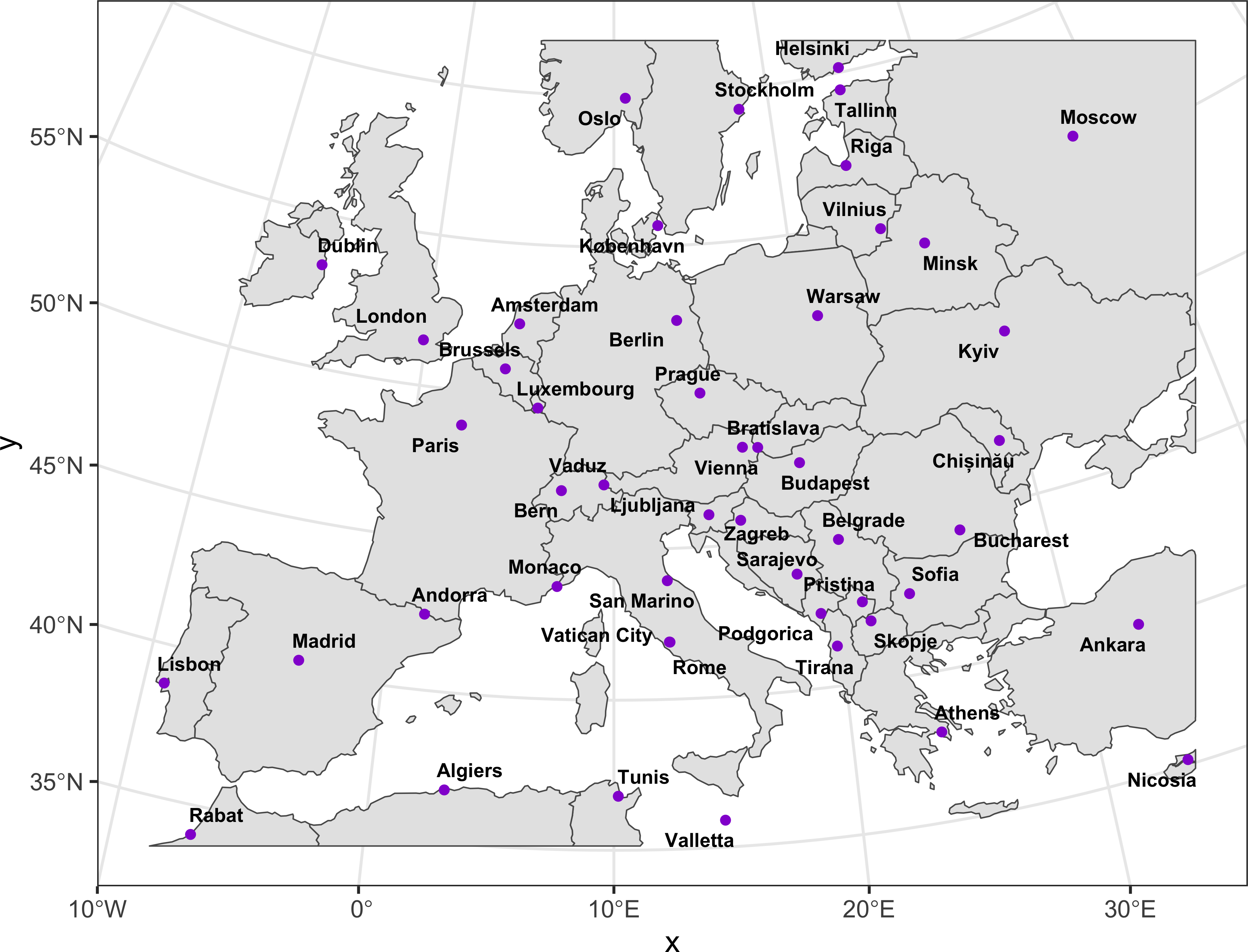

Очевидно, на данную схему можно также дополнительно нанести дополнительно крупные населенные пункты, отобрав их уже по численности населения. Оставим для примера те, в которых живет более \(700 000\) жителей:

major_cities = cities_eu |> 
  filter((FEATURECLA == 'Admin-0 capital') | (POP_MIN >= 700000)) |> 
  mutate(FEATURECLA = ordered(FEATURECLA, levels = unique(cities_eu$FEATURECLA)))


ggplot() +
  geom_sf(data = countries_vw, linewidth = 0.25) +
  geom_sf(data = major_cities, size = 1, color = 'darkviolet') +
  geom_text_repel(data = major_cities, stat = "sf_coordinates",
                size = 2, aes(label = NAME, geometry = geom), 
                box.padding = 0.15, fontface = 'bold') +
  theme_bw()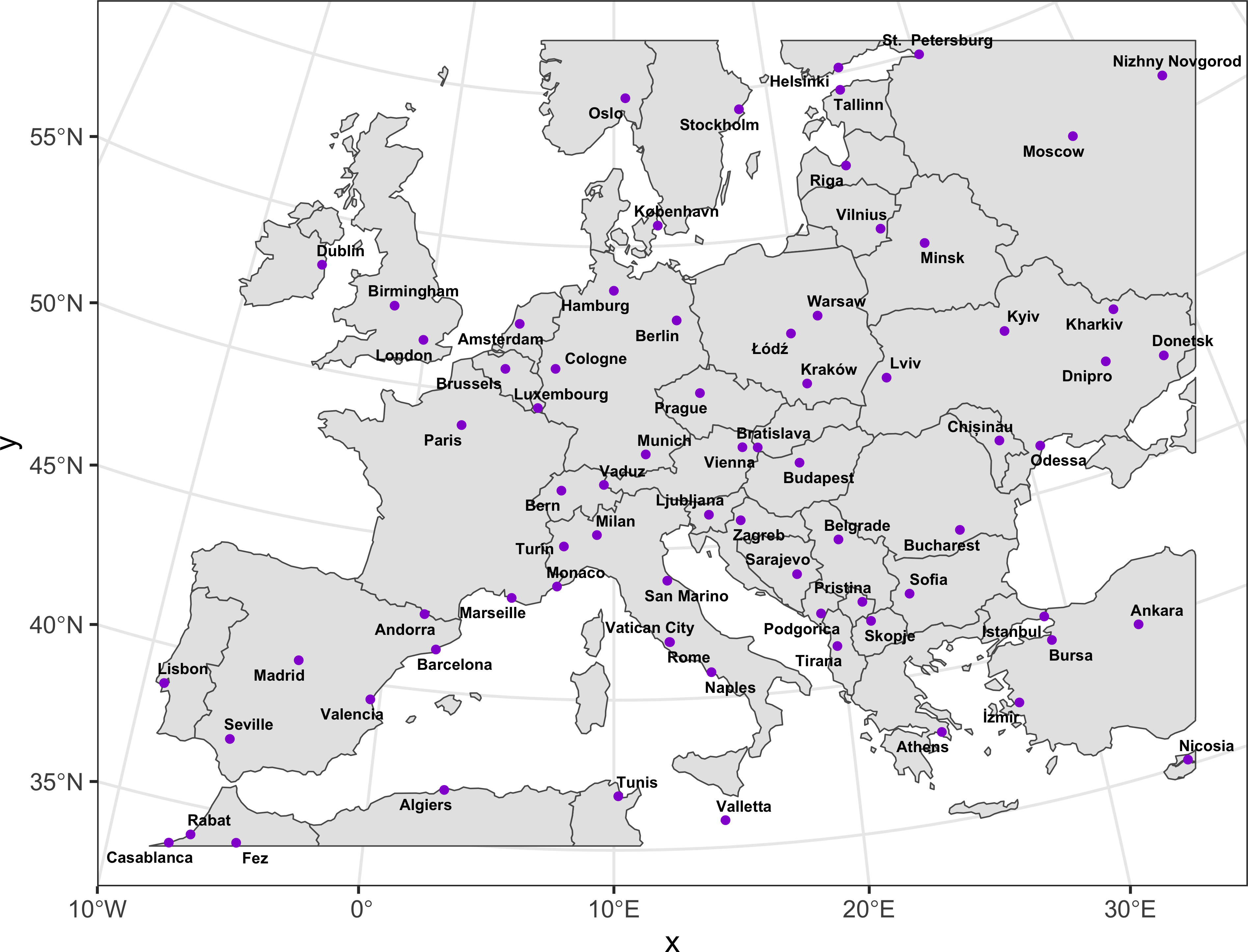

10.7 Классификация объектов по типам

Для того чтобы подчеркнуть отличия между объектами разных типов и значимости, на картах применяется классификация. Более важные объекты показываются более заметными символами, при этом разнотипные, но равные по значимости объекты получают сходные по видимости, но разные по рисунку символы. Пример первого типа — это отображение населенных пунктов разной людности значками разного диаметра. Второй тип классификации на общегеографических картах соответствует, например, автомобильным и железным дорогам.

10.7.1 Вычисляемые классы

В некоторых случаях удобнее не заготавливать классы заранее, а вычислить их непосредственно при отображении, используя заданное преобразование. В частности, такой способ уместен, когда количественный атрибут надо разбить на классы. Например, классифицировать населенные пункты по численности населения и затем назначить им кружки разного диаметра по следующим классам:

• менее 100 000 жителей,
• от 100 000 до 1 000 000 жителей,
• более 1 000 000 жителей

С помощью ggplot это делается путем определения эстетики size и назначения шкалы отображения scale_size_binned. Аналогичным образом варьируется размер шрифта подписи,

brks = c(100000, 1000000)

ggplot() +
  geom_sf(data = countries_vw, size = 0.25) +
  geom_sf(data = capitals, mapping = aes(size = POP_MAX), colour = "black",
          fill = "white",  shape = 21, stroke = 0.5) +
  scale_size_binned(breaks = brks, range = c(1, 3), 
                    name = 'Population, ppl', trans = 'sqrt') +
  new_scale('size') +
  geom_text_repel(data = capitals, stat = "sf_coordinates", force_pull = 1,
                aes(label = NAME, geometry = geom, size = POP_MAX),
                fontface = 'bold', show.legend = FALSE) +
  scale_size_binned(breaks = brks, range = c(2, 3)) +
  scale_x_continuous(expand = c(0,0)) +
  scale_y_continuous(expand = c(0,0)) +
  theme_bw() +
  theme(
    panel.grid = element_line(colour = "black", linewidth = 0.1),
    panel.background = element_rect(fill = NA),
    panel.ontop = TRUE
  ) +
  labs(x = NULL, y = NULL)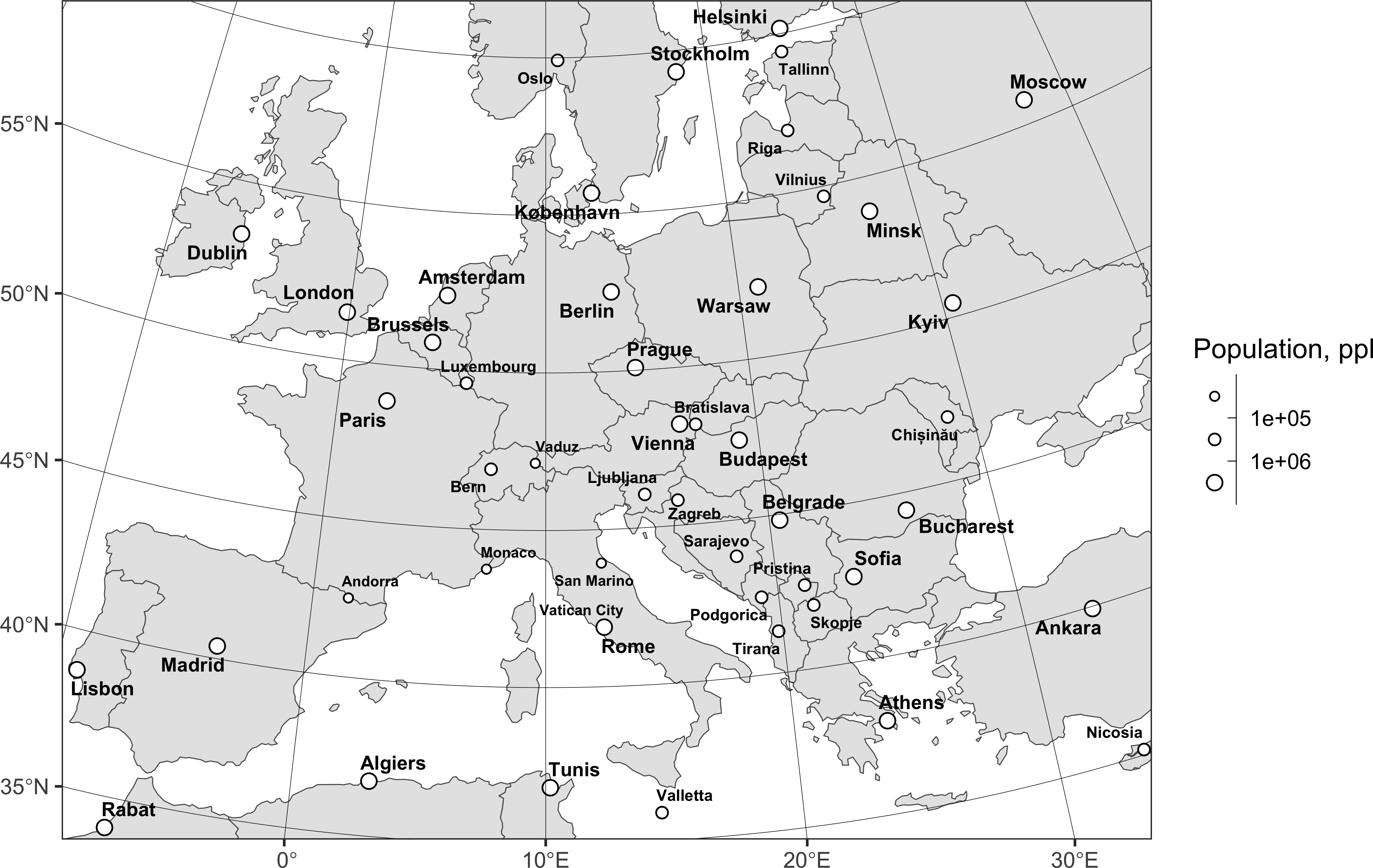

10.7.2 Готовые классы

Если объекты уже наделены классами, их можно непосредственно отобразить на графические переменные. Например, слой дорог в Natural Earth содержит дороги разных классов, а также паромные переправы:

roads = st_read(ne, 'ne_10m_roads', quiet = FALSE) |> 
  st_transform(prj) |> 
  st_crop(box)
## Reading layer `ne_10m_roads' from data source 
##   `/Volumes/Data/Spatial/Natural Earth/natural_earth_vector.gpkg' 
##   using driver `GPKG'
## Simple feature collection with 56600 features and 31 fields
## Geometry type: MULTILINESTRING
## Dimension:     XY
## Bounding box:  xmin: -166.5325 ymin: -55.11212 xmax: 178.4191 ymax: 71.17768
## Geodetic CRS:  WGS 84

plot(roads['type'])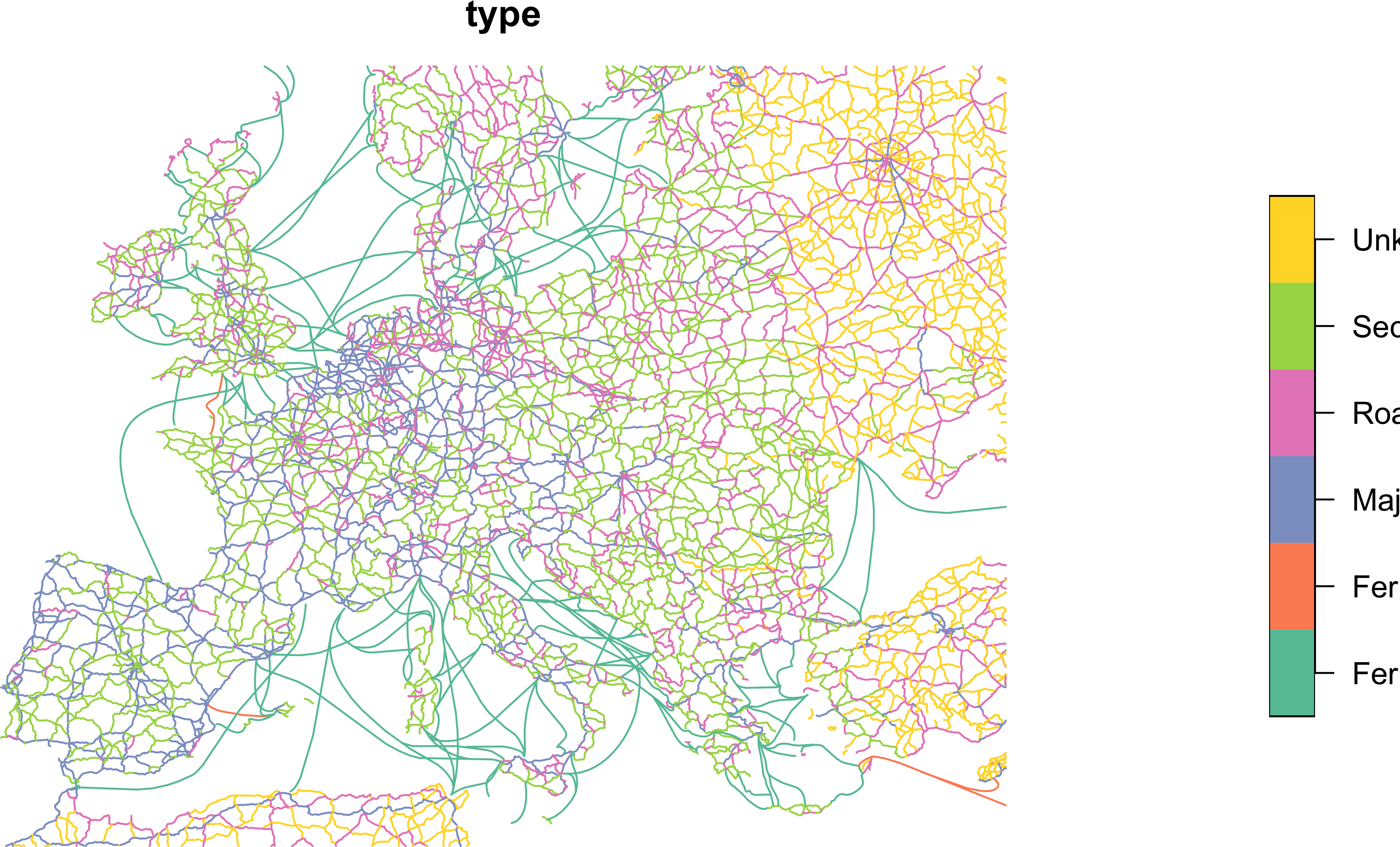

Как правило, дороги отображаются линиями разного цвета и толщины: чем более важна дорога, тем толще будет ее линия и интенсивнее цвет. Попробуем реализовать это средствами ggplot2, при этом ограничим охват территорией Польши, чтобы не перегружать изображение.

auto = roads |> 
  filter(featurecla == 'Road') |> 
  mutate(type = ordered(
    type, 
    levels = c("Unknown", "Road", "Secondary Highway", "Major Highway"))
  )

exp = 75000

box_pl = countries_vw |> 
  filter (SOVEREIGNT == 'Poland') |> 
  st_bbox() +
  c(-exp, -exp, exp, exp) # expand by 50 km each side

ggplot() +
  geom_sf(data = countries_vw, linewidth = 1) +
  geom_sf(data = auto, aes(color = type, linewidth = type)) +
  scale_x_continuous(limits = box_pl[c(1,3)], expand = c(0,0)) +
  scale_y_continuous(limits = box_pl[c(2,4)], expand = c(0,0)) +
  theme_bw()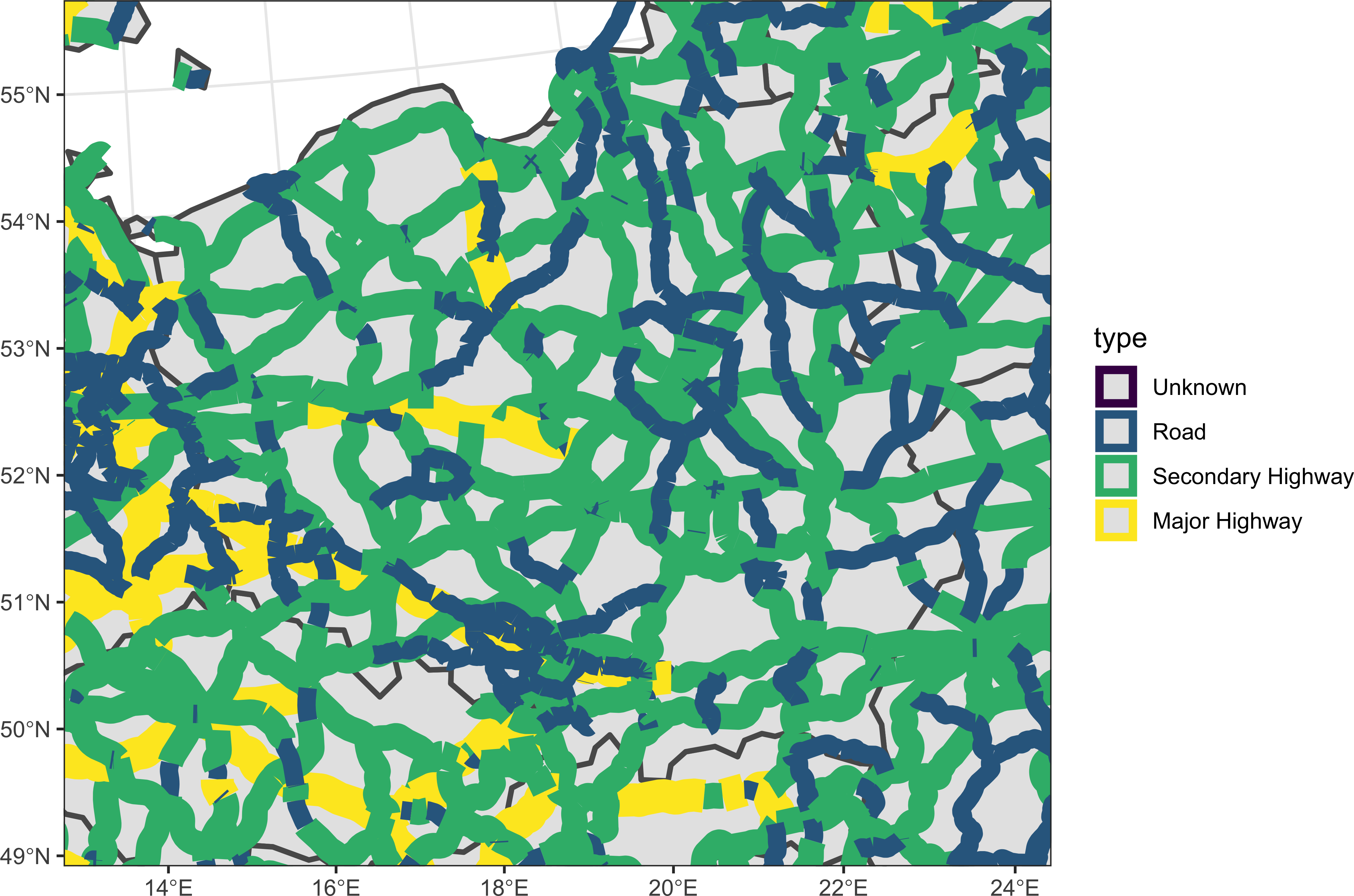

По умолчанию ситуация с символами тревожная, но проблему можно решить путем ручной настройки толщин линий и цветов:

ggplot() +
  geom_sf(data = countries_vw, linewidth = 1) +
  geom_sf(data = auto, aes(color = type, linewidth = type), 
          show.legend = "line") +
  scale_linewidth_ordinal(range = c(0.05, 1), 
                          name = 'Road class',
                          guide = guide_legend(reverse = TRUE)) +
  scale_color_manual(values = c('orange', 'red', 'firebrick', 'darkviolet'), 
                     name = 'Road class',
                     guide = guide_legend(reverse = TRUE)) +
  scale_x_continuous(limits = box_pl[c(1,3)], expand = c(0,0)) +
  scale_y_continuous(limits = box_pl[c(2,4)], expand = c(0,0)) +
  theme_bw()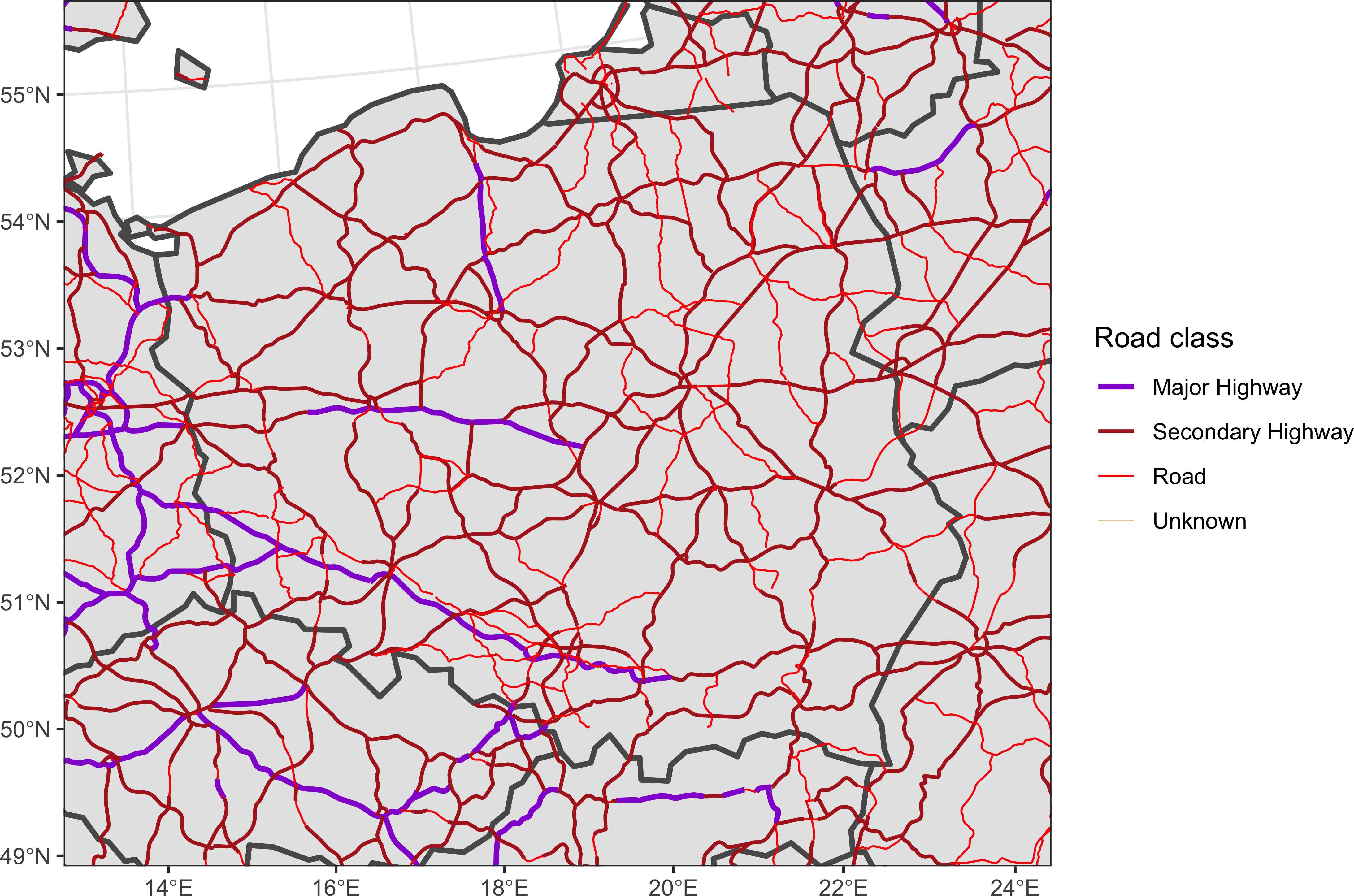

Вернем отображение населенных пунктов, но уже с более дробной классификацией:

options(scipen = 999)
brks = c(100000, 500000, 1000000)

map_pl = ggplot() +
  geom_sf(data = countries_vw, linewidth = 1) +
  geom_sf(data = auto, aes(color = type, linewidth = type), 
          show.legend = "line") +
  scale_linewidth_ordinal(range = c(0.2, 1), 
                          name = 'Road class',
                          guide = guide_legend(reverse = TRUE)) +
  scale_color_manual(values = c('grey20', 'firebrick', 'red', 'darkviolet'), 
                     name = 'Road class',
                     guide = guide_legend(reverse = TRUE)) +
  geom_sf(data = cities_eu, mapping = aes(size = POP_MAX), colour = "black",
          fill = "white",  shape = 21, stroke = 0.5) +
  scale_size_binned(breaks = brks, range = c(1.5, 4), 
                    name = 'Population, ppl', trans = 'sqrt') +
  new_scale('size') +
  geom_label_repel(data = cities_eu, stat = "sf_coordinates", force_pull = 1,
                aes(label = NAME, geometry = geom, size = POP_MAX),
                fontface = 'bold', label.padding=.1, label.size = NA, 
                fill = alpha("white", 0.8), show.legend = FALSE) +
  scale_size_binned(breaks = brks, range = c(2.5, 4), name = 'Population, ppl') +
  scale_x_continuous(limits = box_pl[c(1,3)], expand = c(0,0)) +
  scale_y_continuous(limits = box_pl[c(2,4)], expand = c(0,0)) +
  theme_bw() +
  labs(x = NULL, y = NULL, title = 'Poland')

map_pl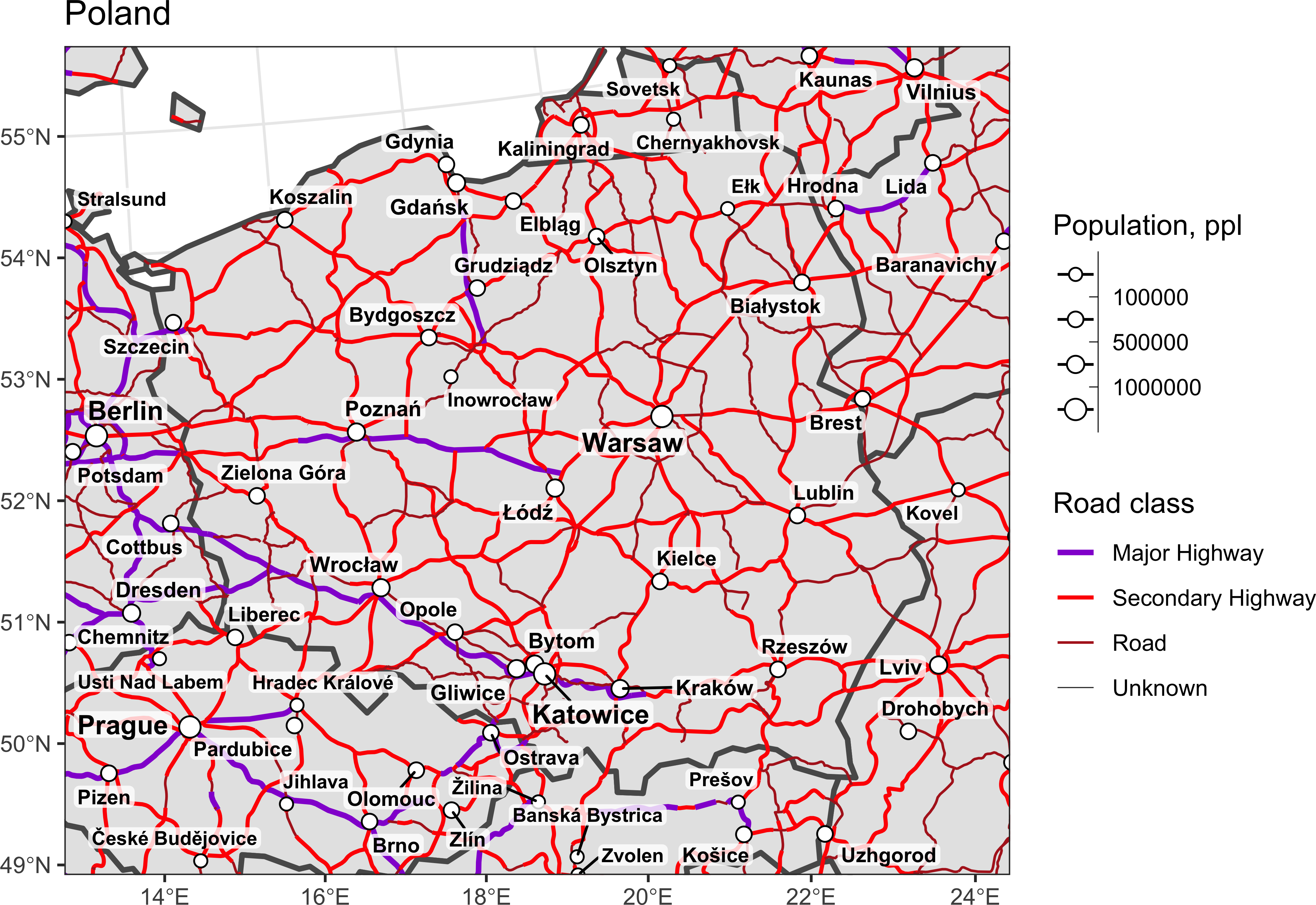

Более сложная ситуация возникает, когда требуется варьировать одновременно несколько графических переменных. Например, если крупнейшие населенные пункты необходимо показывать квадратом, а не кружком. Или автомобильные дороги должны быть толще, чем железные. В этом случае у вас есть два варианта решения проблемы. Вариант “в лоб” — разнести классы объектов по разным слоям и назначить им индивидуальные значки. Вариант более вдумчивый — настроить отображение там образом, чтобы данные брались из одного слоя и классифицировались непосредственно при отображении. Но в этом случае с высокой вероятностью придется делать индивидуальные символы для каждого типа объекта.

10.8 Масштабные линейки и указатели направления на север.

Стандартные элементы компоновки карты — масштабная линейка и указатель на север. С точки зрения ggplot они являются аннотациями. Соответствующие аннотации можно найти в пакете ggspatial.

Масштабную линейку и указатель севера, отображаемые по умолчанию:

map_pl +
  annotation_north_arrow() +
  annotation_scale()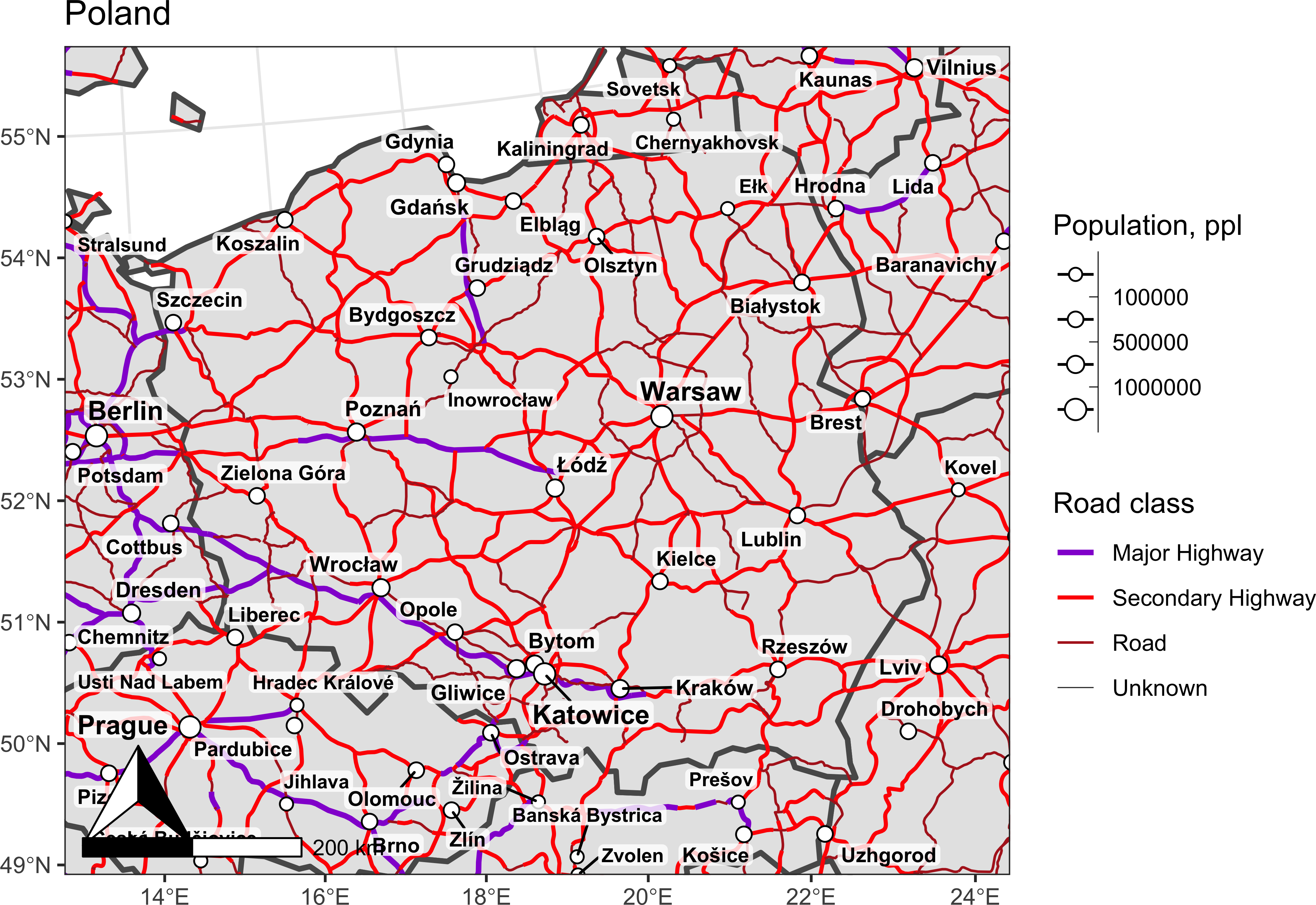

можно кастомизировать, изменив их стиль, размер, расположение и прочие параметры. Например, в данном случае целесообразно переместить их в левый верхний угол и уменьшить в размере:

suppl = list(
  annotation_north_arrow(style = north_arrow_fancy_orienteering(),
                         height = unit(1, 'cm'),
                         width = unit(1, 'cm'),
                         pad_x = unit(0.05, "cm"),
                         pad_y = unit(0.7, "cm"),
                         which_north = "true",
                         location = 'tl'),
  annotation_scale(location = 'tl',
                   style = 'ticks',
                   height = unit(0.1, "cm"),
                   pad_y = unit(0.2, "cm"),
                   pad_x = unit(2.0, "cm"))
)

map_pl + suppl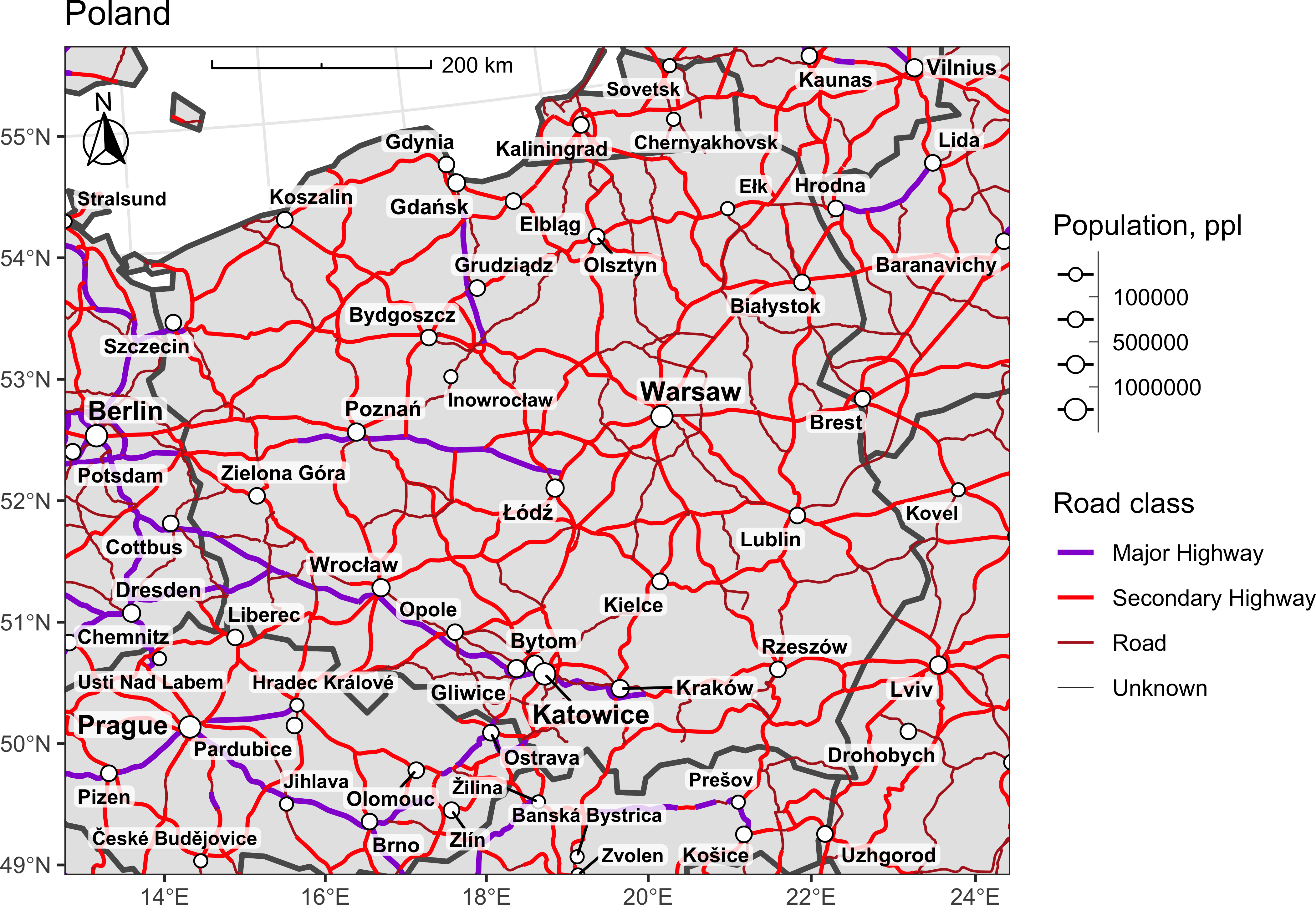

10.9 Карты-врезки

Карты-врезки используются для того чтобы дополнить картографическое изображение пространственной информацией, которая не помещается на основное изображение. Достаточно часто такие карты показывают:

• фрагменты изображаемой территории в более крупном масштабе;
• ту же самую территорию или ее окружение в более мелком масштабе;

При этом с содержательной точки зрения карты-врезки могут как быть идентичными основной карте (показывать те же явления, но в другом масштабе), так и отличаться от нее. Например, на гидрогеологической картах врезки показывают артезианские бассейны для той же территории.

В качестве примера врезки разместим карту Европы, которая показывает местоположение отображаемой страны на карте Европы и выделяет ее другим цветом. Для этого понадобится создать карту-врезку как новый объект ggplot и добавить ее на основную карту на слой аннотаций как объект ggplotGrob.

Начнем с построения карты-врезки:

inset_map = ggplot() +
  geom_sf(data = cnt110, linewidth = 0.25,
          fill = 'grey',
          show.legend = FALSE) +
  geom_sf(data = filter(cnt110, SOVEREIGNT == 'Poland'), 
          fill = 'cyan', linewidth = 1,
          show.legend = FALSE) +
  coord_sf(crs = prj, label_graticule = '',
           xlim = c(box[1], box[3]),
           ylim = c(box[2], box[4])) +
  theme_bw() +
  theme(panel.background = element_rect(fill = 'azure'),
        plot.margin = margin(0, 0, 0, 0, "cm"))

inset_map

Теперь разместим ее в одном из углов. Поскольку мы знаем ограничивающий прямоугольник отображаемой области, это сделать можно путем аффинных преобразований относительно выбранного угла карты. Например, относительно левого нижнего:

lowleft = box_pl[c(1,2,1,2)] # левый нижний угол
ratio = (box[4] - box[2]) / (box[3] - box[1]) # пропорции карты-врезки
dx = box_pl[3] - box_pl[1] # ширина основной карты

# высота основной карты, как если бы она имела 
# такие же пропорции, как и врезка
dy = dx * ratio 

# Находим ограничивающий прямоугольник врезки
# Которая будет иметь длину стороны 0,25 от длины карты

box_ins = 0.25 * c(0, 0,  dx, dy) + lowleft 

# собираем аннотацию 
inset = annotation_custom(
    grob = ggplotGrob(inset_map),
    xmin = box_ins[1], xmax = box_ins[3],
    ymin = box_ins[2], ymax = box_ins[4]
)

map_pl +
  suppl +
  inset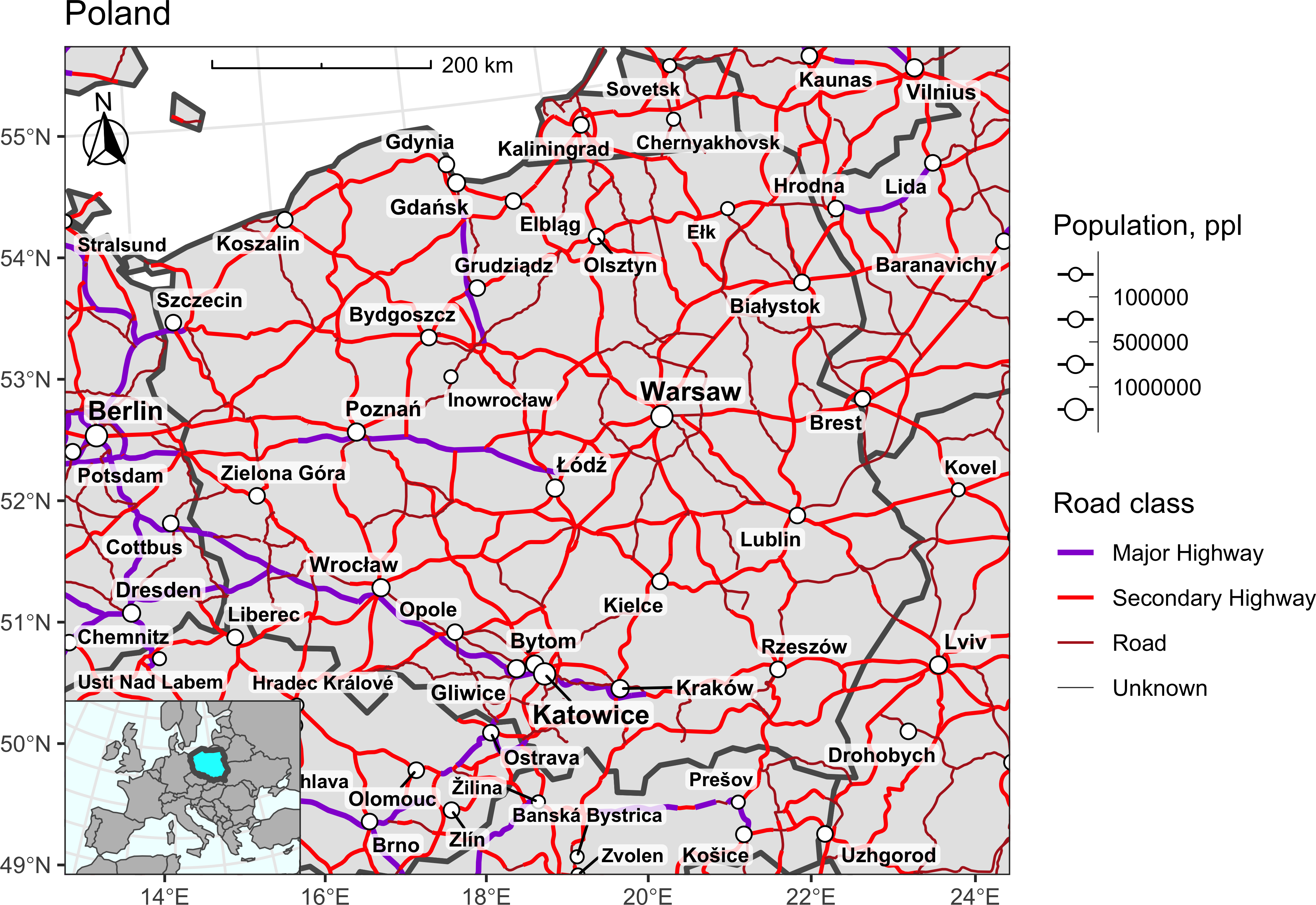

Код построения карты-врезки целесообразно вынести в функцию для последующего использования:

annotation_inset = function(map, inset, scale = 0.25, rx = 0, ry = 0, scaledir = 'auto') {
  
  # Scale limits for main map
  xlim = ggplot2::ggplot_build(map)$layout$panel_params[[1]]$x_range
  ylim = ggplot2::ggplot_build(map)$layout$panel_params[[1]]$y_range
  
  # Scale limits for inset map
  xlim_ins = ggplot2::ggplot_build(inset)$layout$panel_params[[1]]$x_range
  ylim_ins = ggplot2::ggplot_build(inset)$layout$panel_params[[1]]$y_range
  
  if (scaledir == 'auto') {
    along_x = diff(xlim)/diff(ylim) < diff(xlim_ins)/diff(ylim_ins)
    scaledir = ifelse(along_x, 'x', 'y')
    message('Scaling inset along ', scaledir, ' axis')
  } else if (! (scaledir %in% c('x', 'y'))) {
    stop('scaledir should be one of "auto", "x" or "y"')
  }
    
  if (scaledir == 'x') {
    ratio = diff(ylim_ins) / diff(xlim_ins)
    xmax = diff(xlim)
    ymax = xmax * ratio 
  } else {
    ratio = diff(xlim_ins) / diff(ylim_ins)
    ymax = diff(ylim)
    xmax = ymax * ratio 
  }
  
  lowleft = c(xlim[1], ylim[1], xlim[1], ylim[1])
  
  box = scale * c(0, 0,  xmax, ymax) + lowleft

  dx = rx * (xlim[2] - box[3])
  dy = ry * (ylim[2] - box[4])
  
  ggplot2::annotation_custom(
      grob = ggplot2::ggplotGrob(inset),
      xmin = box[1] + dx, xmax = box[3] + dx,
      ymin = box[2] + dy, ymax = box[4] + dy
  )
  
}

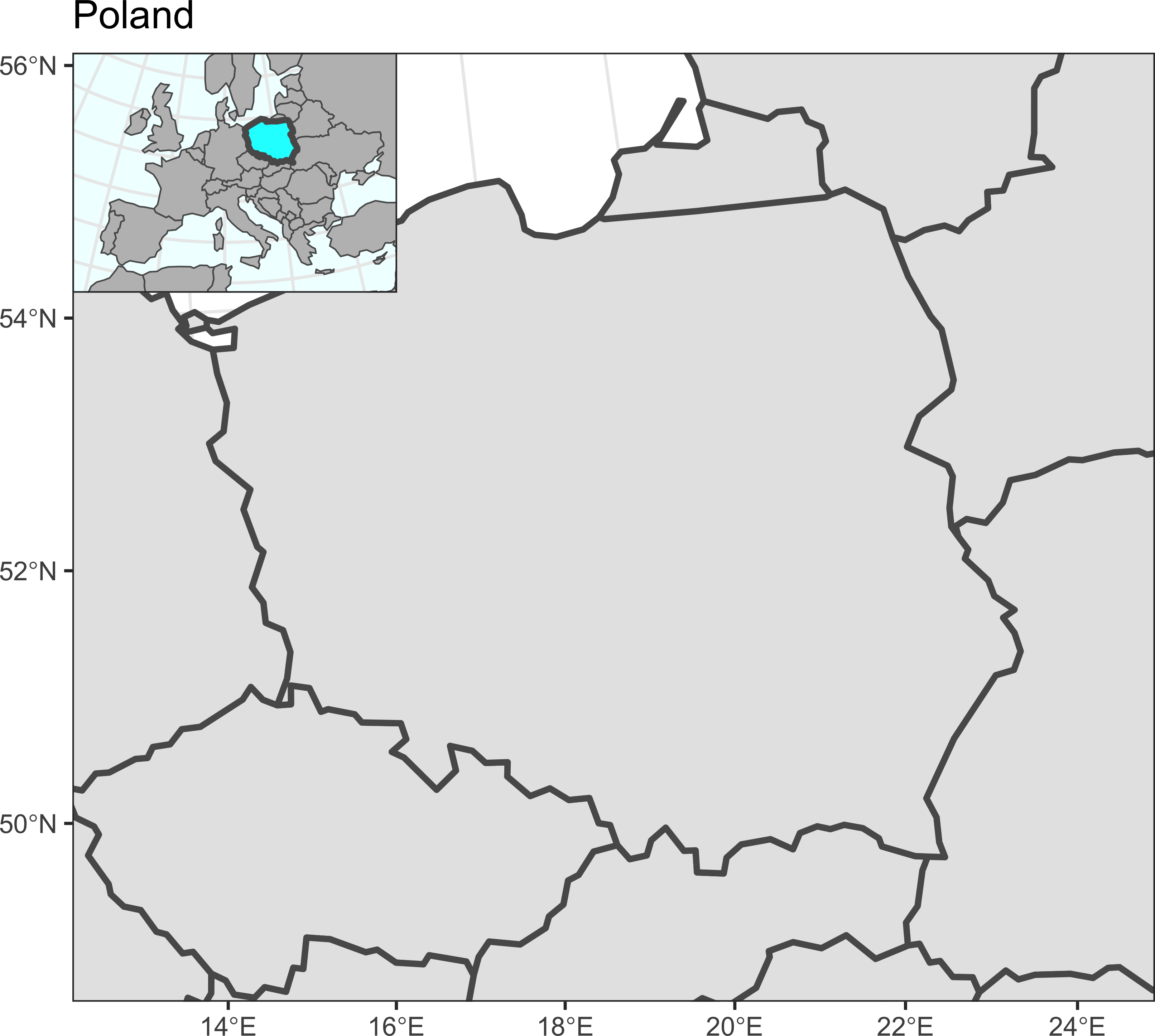
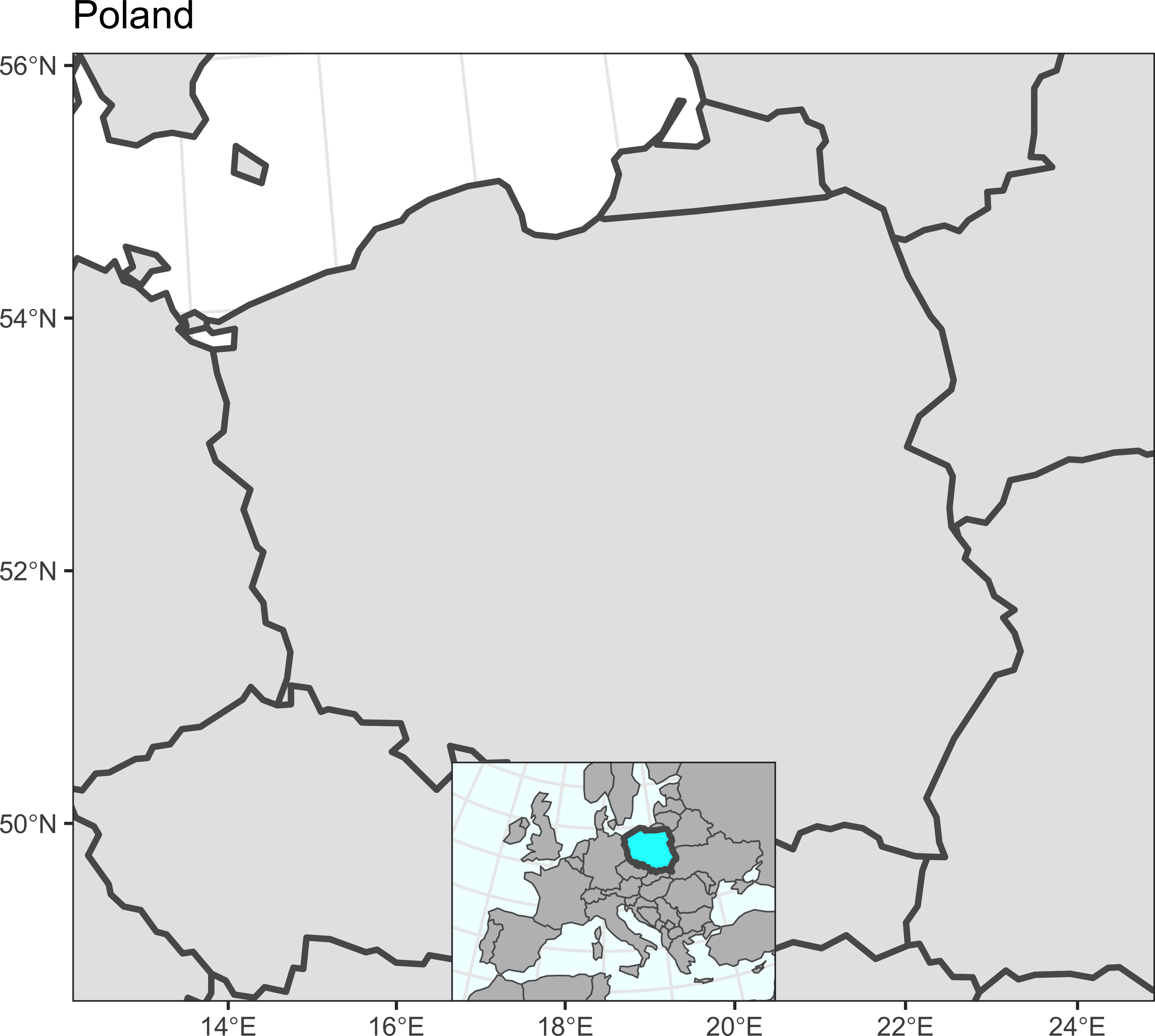
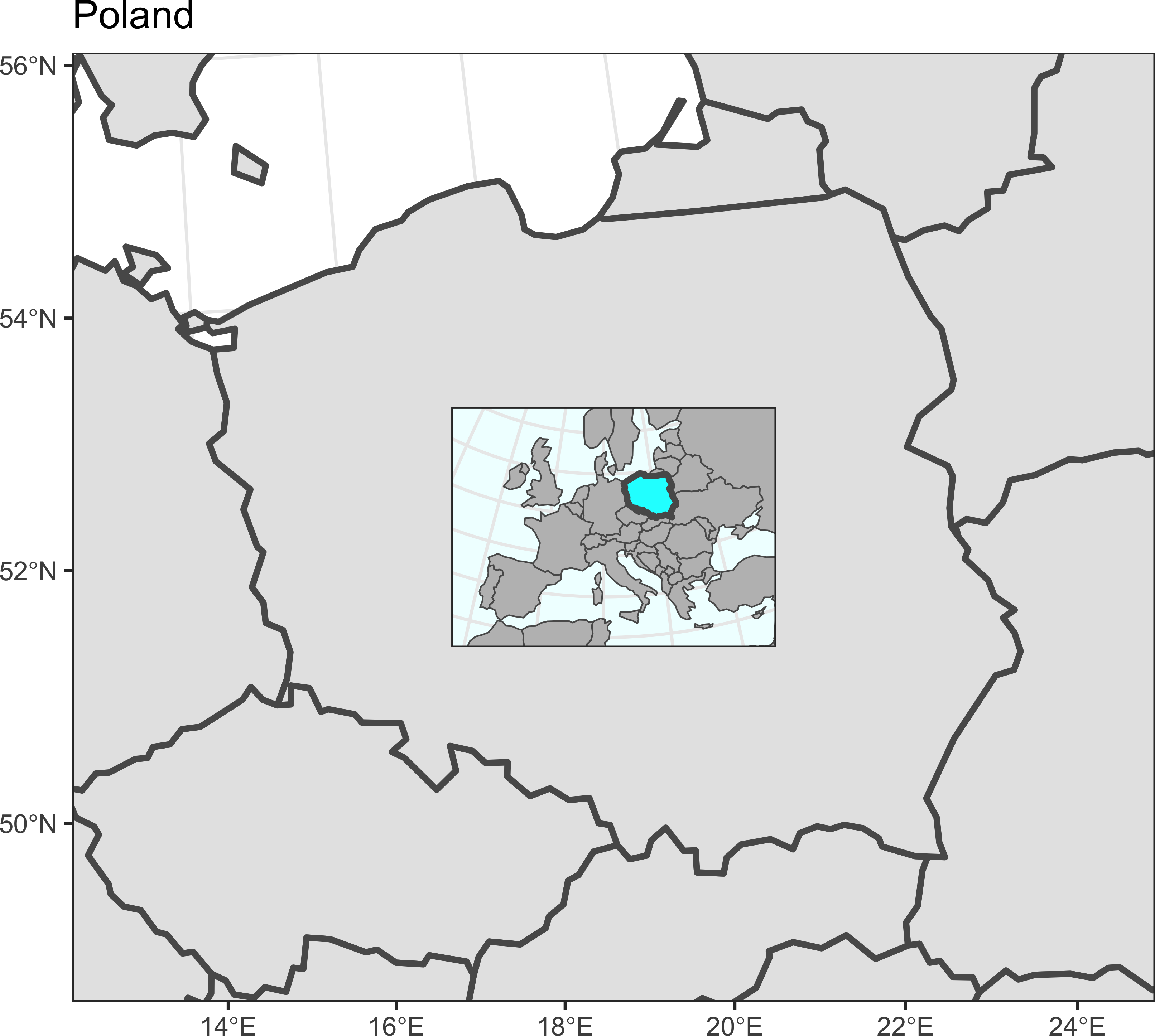
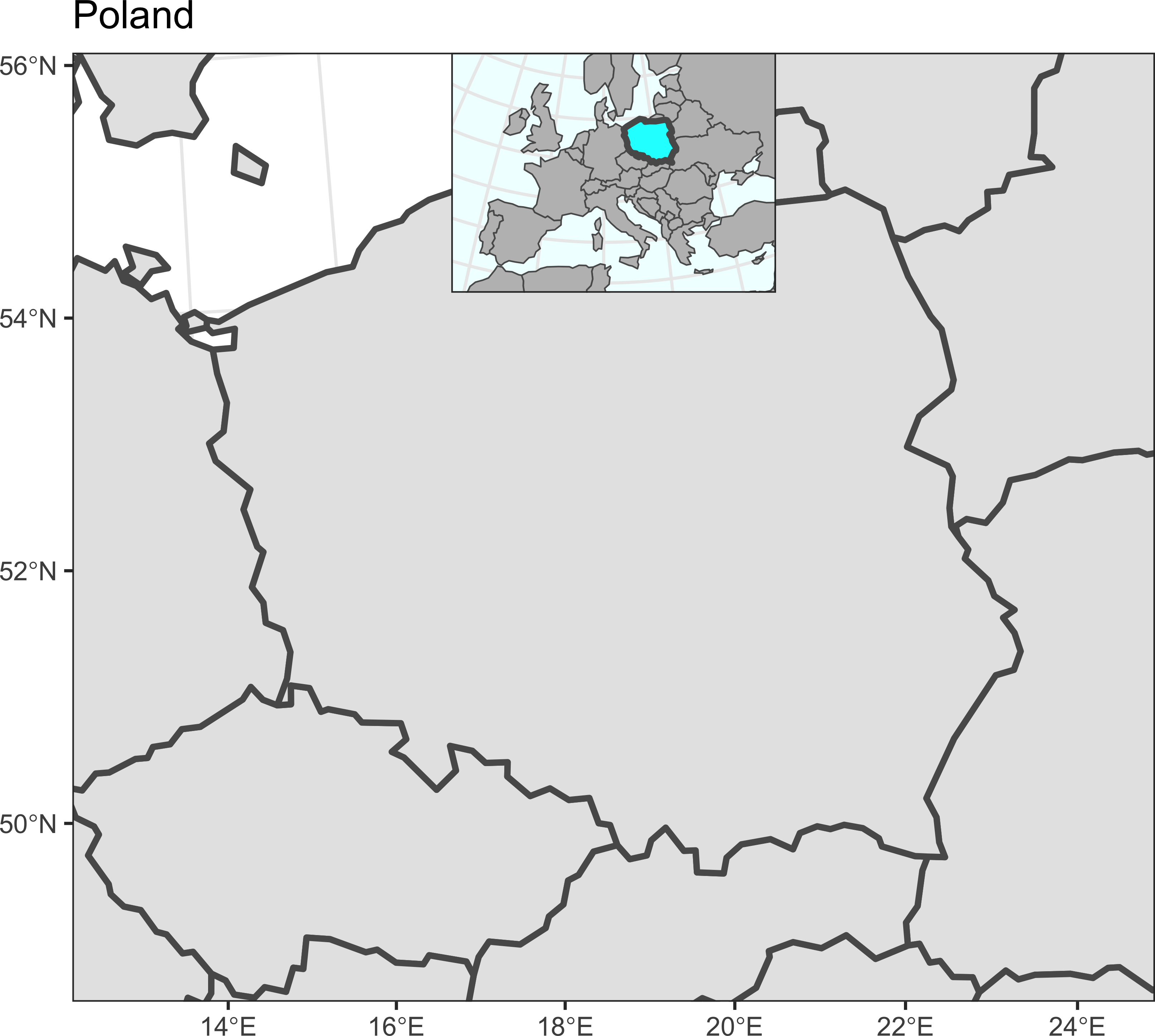
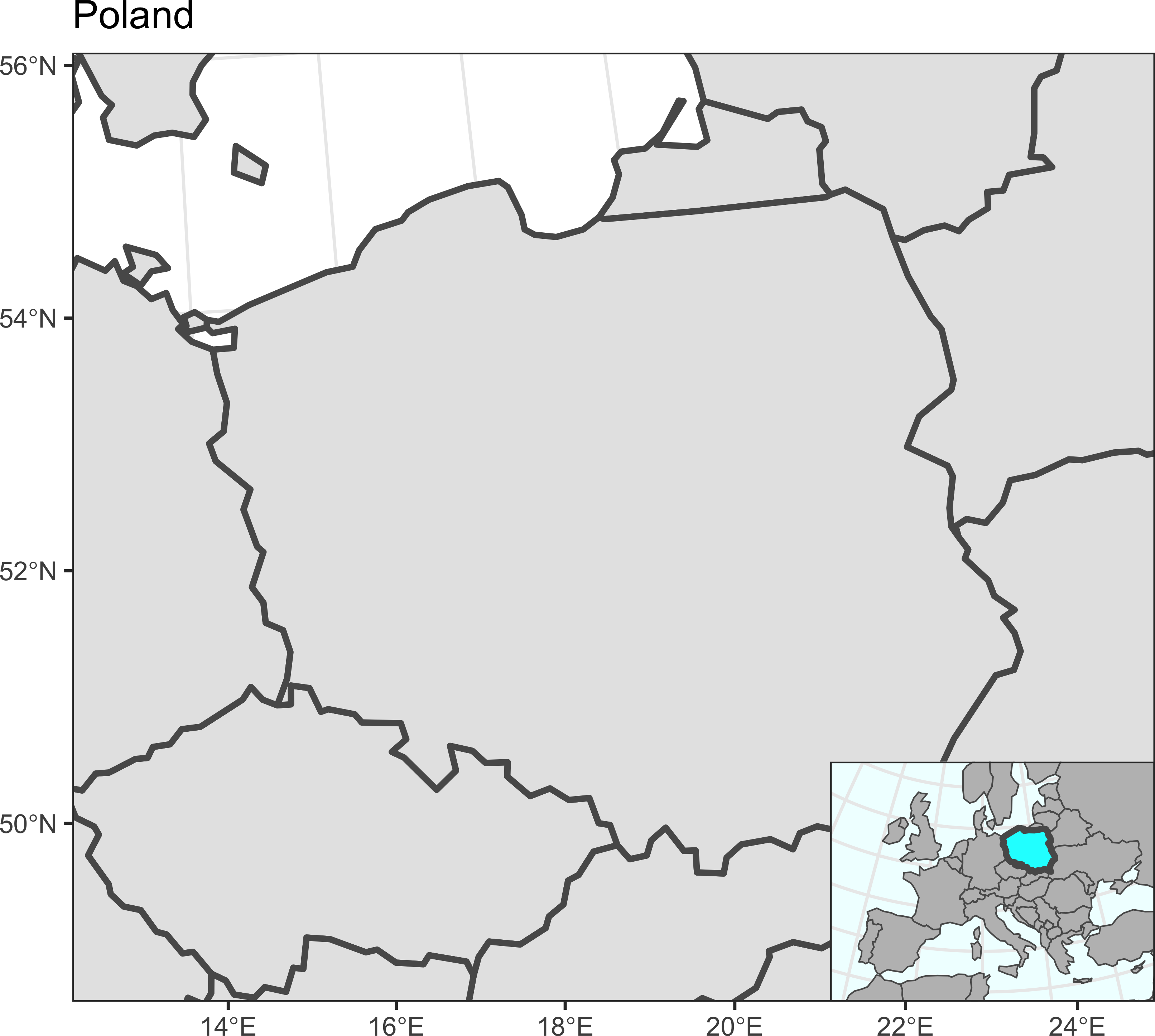
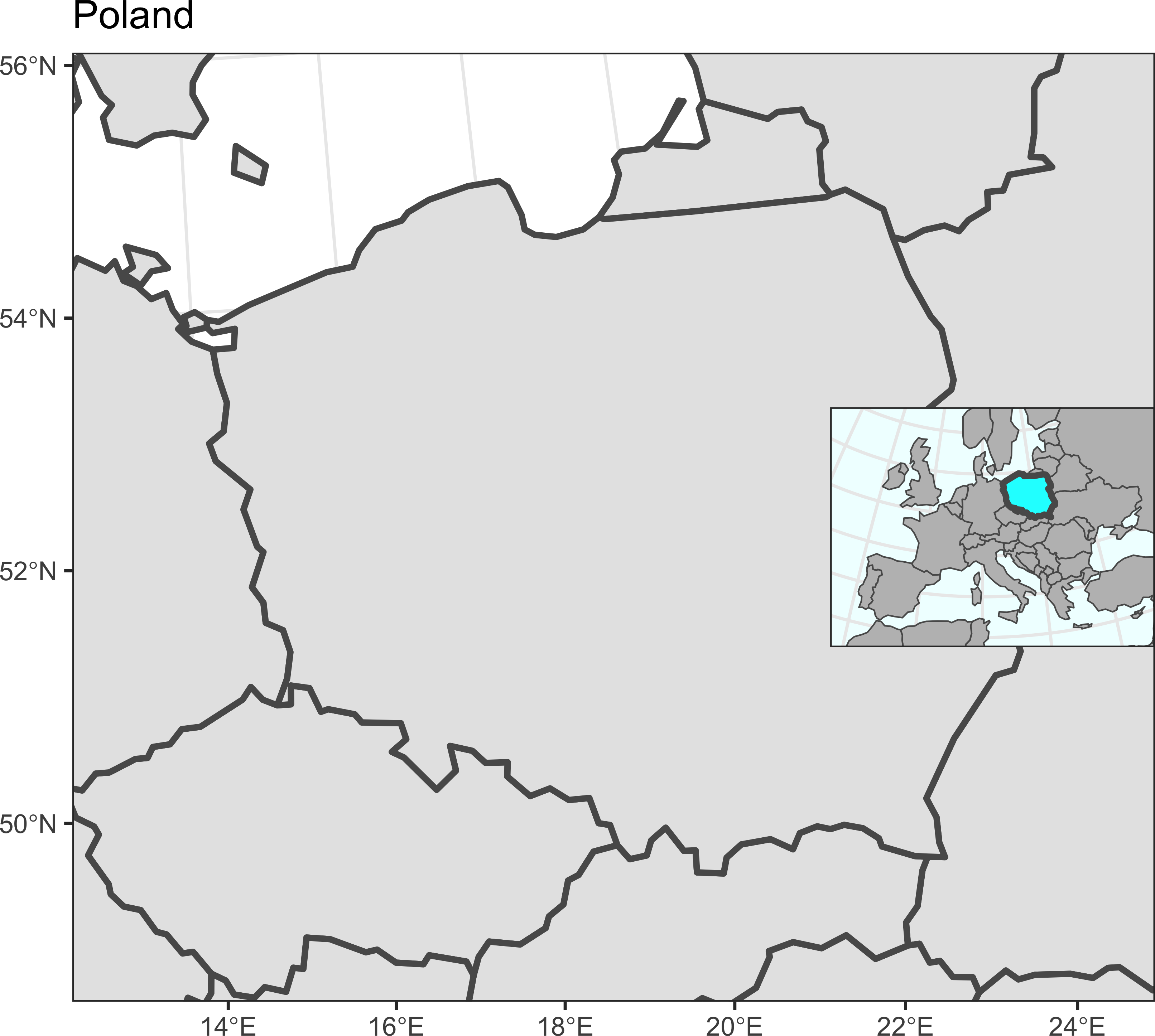
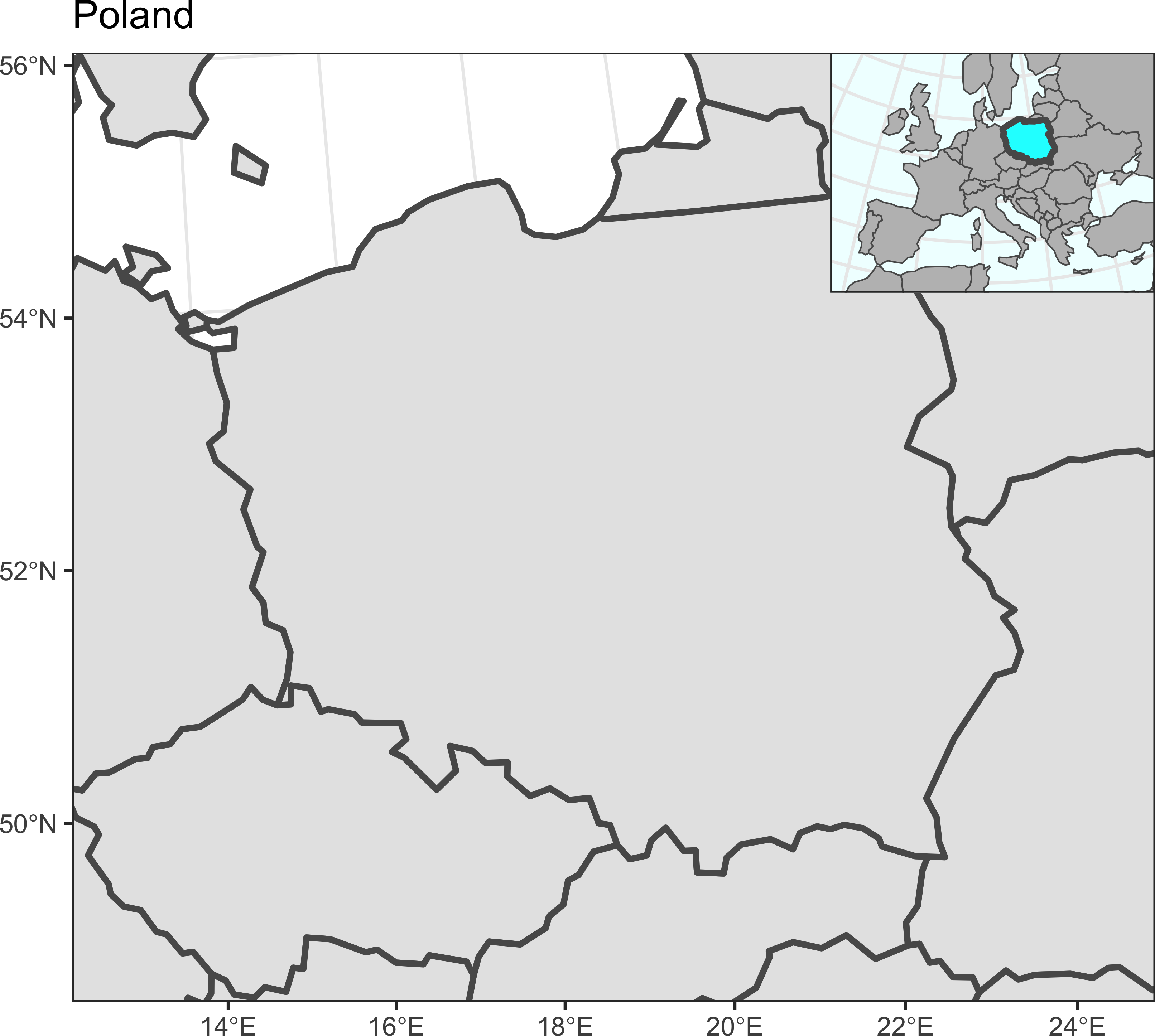
Прооверим работоспособность для 9 разных местоположений карты-врезки:

map_simple = ggplot() +
  geom_sf(data = countries_vw, linewidth = 1) +
  scale_x_continuous(limits = box_pl[c(1,3)]) +
  scale_y_continuous(limits = box_pl[c(2,4)]) +
  theme_bw() +
  labs(x = NULL, y = NULL, title = 'Poland')

for (i in 0:2 / 2) 
  for (j in 0:2 / 2)
    print(map_simple + annotation_inset(map_simple, inset_map, 0.3, i, j))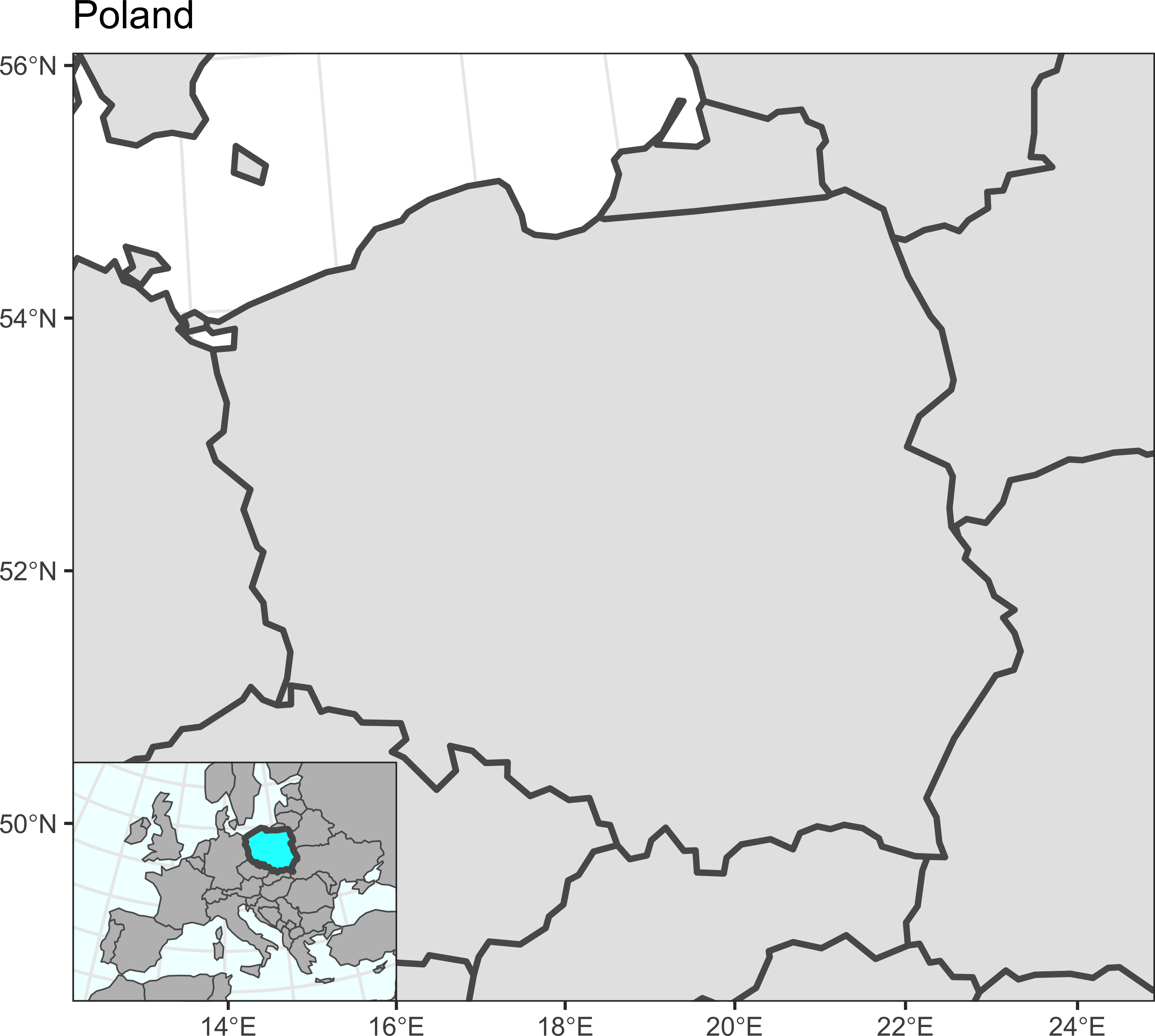

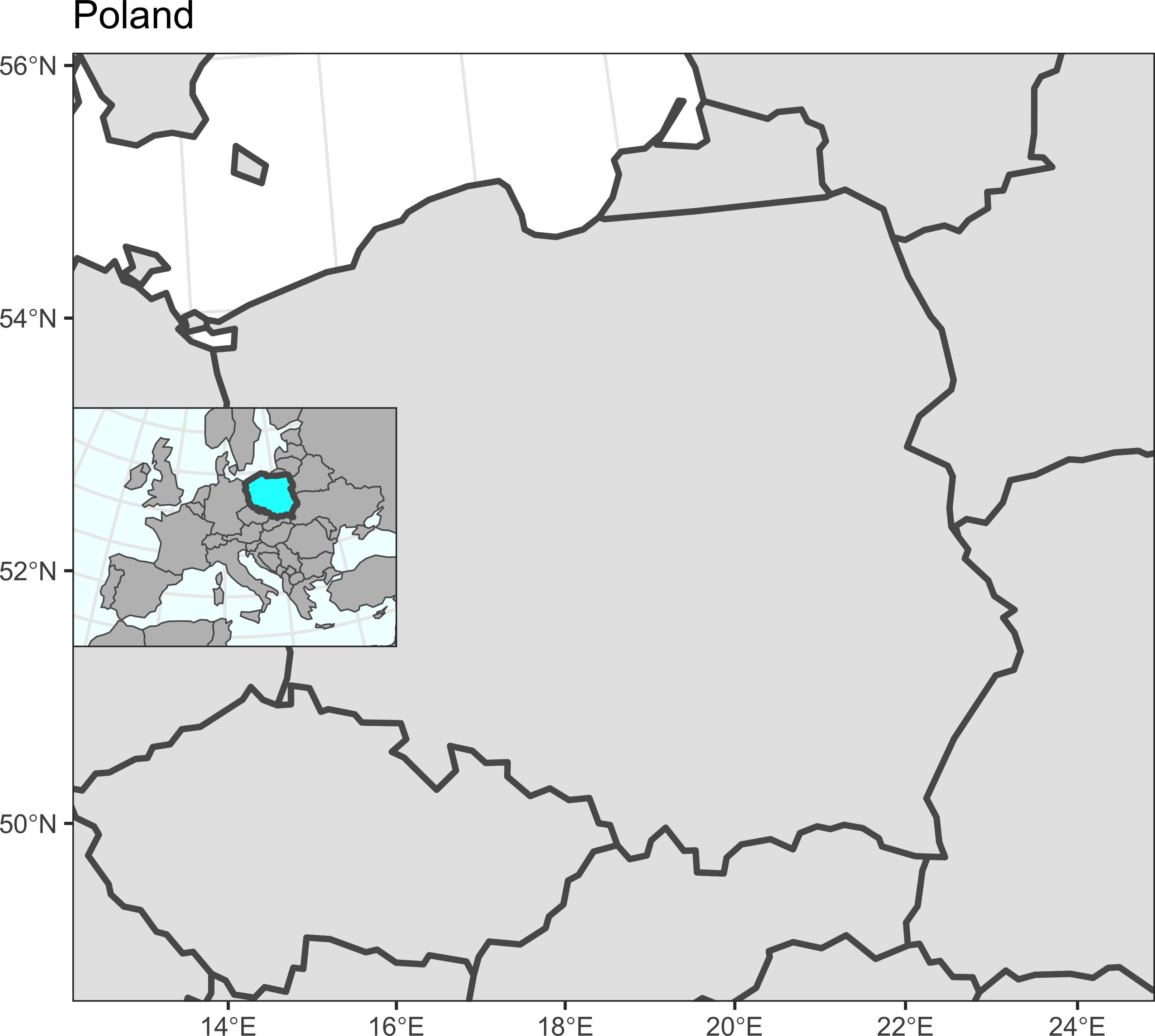
10.10 Краткий обзор

Для просмотра презентации щелкните на ней один раз левой кнопкой мыши и листайте, используя кнопки на клавиатуре:

Презентацию можно открыть в отдельном окне или вкладке браузере. Для этого щелкните по ней правой кнопкой мыши и выберите соответствующую команду.

10.11 Контрольные вопросы и упражнения

10.11.1 Вопросы

1. Какие типы геометрии ggplot2 позволяют визуализировать данные типа sf и stars?
2. Перечислите масштабы (уровни детализации), на которых доступны данные Natural Earth.
3. Нужно ли для отображения карт средствами ggplot2 выполнять предварительное проецирование всех слоев в единую проекцию? Если нет, то каким образом можно задать желаемую проекцию отображения? Будет ли работать этот подход с растровыми данными?
4. Объясните, как избежать возникновения ложных участков границ и береговых линий при визуализации карт мира.
5. Какие приемы можно использовать для того чтобы обеспечить хорошую читаемость подписей на карте, нагруженной границами?
6. Какая функция позволяет строить координатную сетку в виде викторных объектов?
7. Что необходимо сделать с ограничивающим прямоугольником географической системы координат \([-180; 180] \times [-90; 90]\), состоящим из 4 точек, чтобы его границы изгибались по внешней границе карты в соответствии проекцией? Какую функцию необходимо применить для этого?
8. При визуализации рельефа гипсометрическим способом отрицательные высоты на суше и на море показываются разными цветам. Если у вас сплошная цифровая модель рельефа на сушу и море в виде объекта stars, как можно добиться этого эффекта?
9. Какая функция пакета rmapshaper позволяет выполнять геометрическое упрощение линий и полигонов? В чем визуальный недостаток линий, упрощенных алгоритмом Дугласа-Пейкера? Какой алгоритм лучше использовать для геометрического упрощения вместо него?
10. Объясните, как можно добиться того, чтобы точки пересечения (касания) объектов двух слоев оставались неподвижными при геометрическом упрощении (т.е. сохранялась топология объектов).
11. Если на карте точечные объекты (например, населенные пункты) размещены слишком густо, как можно добиться их прореживания?

10.11.2 Упражнения

1. Скачайте базу данных и цифровую модель рельефа на территорию Сатинского полигона МГУ. Изучите содержимое базы данных и постройте на основе этих данных общегеографическую карту средствами ggplot2 в проекции UTM.

   Опционально: сделайте на карте врезку, которая показывает расположение полигона точкой на мелкомасштабной карте (в качестве основы используйте данные Natural Earth).

2. Используя возможности ggplot2, и данные Natural Earth масштаба 10M, создайте политико-административную и физическую карты Африки в азимутальной равновеликой проекции. Определите самостоятельно необходимые для этого слои. В качестве данных о рельефе для физической карты скачайте цифровую модель рельефа GEBCO, оптимизированную для отображения в соответствующих масштабах.

Самсонов Т.Е. Визуализация и анализ географических данных на языке R. М.: Географический факультет МГУ, 2023. DOI: 10.5281/zenodo.901911